포털:수학
Portal:Mathematics
수학은 추상적인 물체(숫자, 점, 공간, 세트, 구조, 게임 등)에 대한 표현과 추론을 연구하는 학문이다.수학은 자연과학, 공학, 의학, 그리고 사회과학을 포함한 많은 분야에서 필수적인 도구로 전세계에서 사용되고 있다.다른 분야에 수학적 지식을 적용하는 것과 관련된 수학의 분야인 응용수학은 새로운 수학 발견에 영감을 주고 활용하며 때로는 통계학이나 게임 이론과 같은 완전히 새로운 수학적 학문의 발달로 이어진다.수학자들도 아무런 응용도 염두에 두지 않고 순수 수학, 즉 그 자체를 위해 수학에 종사한다.순수 수학과 응용 수학을 구분하는 명확한 선이 없고, 순수 수학으로 시작된 것에 대한 실용적 응용이 자주 발견된다.(전체 기사...)
여기에 소개된 기사들이 전시되어 있는데, 이것은 영어 위키백과에서 가장 좋은 내용 중 일부를 나타낸다.
수학에서 집단은 어떤 두 원소를 결합하여 제3 원소를 형성하는 연산을 갖춘 집합으로, 연산이 연상되고, ID 요소가 존재하며, 모든 원소가 역성을 갖는 방식이다.그룹 공리라고 불리는 이 세 가지 조건은 숫자 체계와 많은 다른 수학적 구조를 유지한다.예를 들어, 정수와 덧셈 연산이 함께 그룹을 형성한다.집단의 개념과 집단의 공리를 통한 그 정의는 매우 다른 수학적 성질(숫자, 기하학적 모양, 다항식 뿌리 등)의 본질적인 구조적 특성을 통일적으로 다루기 위해 정교하게 기술되었다.수많은 영역(수학 내외)의 집단이 편재하기 때문에 일부 저자들은 이를 현대 수학의 중심 조직 원리로 여긴다.
집단은 대칭과 기하학적 변환의 연구를 위한 기하학에서 자연적으로 발생한다: 개체의 대칭 그룹이라고 불리는 집단을 형성하는 물체의 대칭과 주어진 형태의 변환은 일반적으로 집단을 형성한다.이러한 예는 (갈루아 그룹과 함께) 집단의 개념의 기원에 있었다.거짓말 그룹은 기하학에서 대칭 그룹으로 발생하지만 입자 물리학의 표준 모델에도 나타난다.푸앵카레 그룹은 특수상대성이론에서 스페이스타임의 대칭으로 구성된 리 그룹이다.점 그룹은 분자 화학에서 대칭을 묘사한다. (전체 기사...)- 포르투갈 비블리오테카 나시오날 드 포르투갈의 소장품 중 1634년판 후스의 트랙라투스 드 글로비스의 제목 페이지
로버트 후스(Robert Hues, 1553년 – 1632년 5월 24일)는 영국의 수학자 및 지리학자였다.그는 세인트루이스에 다녔다. 옥스퍼드 대학의 메리 홀, 그리고 1578년에 졸업했다.Hues는 지리학과 수학에 관심을 갖게 되었고, Walter Raleigh가 설립한 학교에서 항해학을 공부했다.뉴펀들랜드로 여행하는 동안, 그는 나침반의 변화에 대해 받아들여지는 출판된 가치들을 의심하게 하는 관찰을 했다.1586년에서 1588년 사이에, Hues는 지구 순환을 위해 Thomas Cavendish와 함께 여행했고, 천문학적인 관측을 수행했고 그들이 방문한 장소의 위도를 측정했다.1591년 8월부터, Hues와 Cavendish는 다시 지구의 또 다른 순환 여행을 시작했다.항해를 하는 동안, 후스는 남대서양에서 천문학적 관측을 했고, 다양한 위도와 적도에서의 나침반의 변화에 대한 관찰을 계속했다.카벤디쉬는 1592년 여행 중 사망했고, 후스는 이듬해 영국으로 돌아왔다.
1594년, 후스는 1592년 말이나 1593년 초에 에메리 몰리뉴스가 만들어 간행한 지상 및 천상의 글로브의 용도를 설명하고, 영국 선원들이 실용적인 천문 항해를 하도록 장려하기 위해 작성한 라틴어 작품 《Tractatus de Globis et Eorum usu》(Treates on Globes and Thats Usu)에 그의 발견을 발표하였다.ation. Hues의 작업은 이후 네덜란드어, 영어, 프랑스어, 라틴어로 된 적어도 12개의 인쇄물에 들어갔다. (전체 기사...)
마리안 아담 레제프스키(Parian Adam Rejewski, [listenmarjan rɛjɛfskʲi](듣기; 1905년 8월 16일 ~ 1980년 2월 13일)는 폴란드 수학자 겸 암호학자로, 1932년 말 프랑스 군사 정보기관이 입수한 제한된 문서에 의해 도움을 받았다.그 후 거의 7년 동안 레제프스키와 동료 수학자-암호학자 제르지 로이키와 헨리크 지갈스키는 독일인들이 그들의 장비와 암호화 절차에 수정을 도입했을 때 조차도 독일 기계 암호를 해독하기 위해 기술과 장비를 개발하고 사용했다.제2차 세계대전이 발발하기 5주 전, 폴란드인들은 바르샤바에서 열린 회의에서 그들의 업적을 프랑스, 영국인들과 공유했고, 따라서 영국은 르제프스키가 기계를 처음 재구성한 지 7년 만에 독일 에니그마 암호화된 메시지를 읽기 시작할 수 있었다.영국인들이 에니그마의 암호 해독을 통해 얻은 정보는 코드명 울트라(Ultra)의 일부를 형성했고 아마도 결정적으로 독일의 패배에 기여했다.
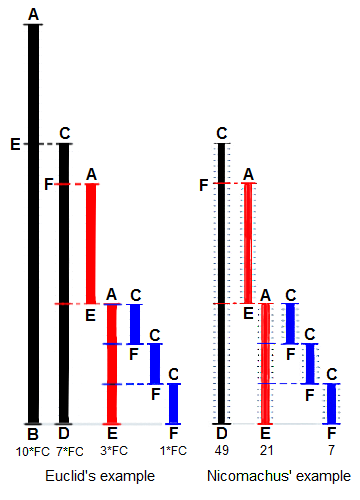
레제프스키는 1929년 포즈나 대학에서 수학을 공부하던 중 1932년 9월에 합류한 폴란드 총참모부 암호국(Biuro Szyfrow)에서 실시한 비밀 암호학 강좌에 참석했다.FBI는 1932년 말에 에니그마가 수신한 메시지를 읽는 데 성공하지 못했고 르젭스키가 이 문제를 해결하도록 했다; 그는 불과 몇 주 후에 이 기계의 비밀 내부 배선을 추론했다.그리고 나서 Rejewski와 그의 두 동료들은 에니그마 메시지의 규칙적인 암호 해독을 위한 연속적인 기술을 개발했다.그 자신의 공헌에는 그가 발명한 사이클로미터를 이용해 도출한 암호 카드 카탈로그와 암호 폭탄이 포함되어 있었다. (전체 기사...)- 두 개의 시작 길이 BA와 DC 중 가장 큰 공통 구분자(GCD)를 찾는 유클리드 방법은 둘 다 공통 "단위" 길이의 배수로 정의된다.길이 DC가 짧으면 BA를 "측정"하는데 사용되지만, 나머지 EA가 DC보다 작기 때문에 단 한 번만. EA는 이제 짧은 길이의 DC를 측정(두 배), 나머지 FC는 EA보다 짧다.그런 다음 FC는 길이 EA를 측정한다.남은 게 없기 때문에 FC가 GCD가 되는 것으로 마무리된다.오른쪽의 니코마쿠스의 예에서 49와 21은 GCD가 7(히스 1908:300에서 파생됨)이 된다.
수학에서 유클리드 알고리즘, 즉 유클리드 알고리즘은 두 정수(숫자)의 가장 큰 공통분할기(GCD)를 계산하는 효율적인 방법인데, 이 두 정수(숫자)를 나머지 없이 모두 나누는 수가 가장 많다.그것은 고대 그리스 수학자 유클리드(Eucleid)의 이름을 따서 지어졌는데, 그는 이것을 그의 원소(C. 300 BC)에서 처음 묘사했다.
알고리즘의 예로서, 잘 정의된 규칙에 따라 계산을 수행하기 위한 단계별 절차,
그리고 공통적으로 사용되는 가장 오래된 알고리즘 중 하나이다.분수를 가장 단순한 형태로 줄이는 데 사용할 수 있으며, 다른 많은 숫자-이론적 및 암호 계산의 일부분이다.
유클리드 알고리즘은 더 큰 숫자가 더 작은 숫자와의 차이로 대체되는 경우 두 숫자의 가장 큰 공통점수는 변하지 않는다는 원리에 기초한다.예를 들어, 21은 252와 105의 GCD(252 = 21 × 12, 105 = 21 × 5)이며, 같은 숫자 21도 105와 252 - 105 = 147이다.이 대체는 두 숫자 중 더 큰 숫자를 감소시키기 때문에, 이 과정을 반복하면 두 숫자가 같아질 때까지 연속적으로 더 작은 수의 쌍을 갖게 된다.그것이 발생할 때, 그것들은 원래 두 숫자의 GCD이다.단계를 역행하거나 확장된 유클리드 알고리즘을 사용하여 GCD는 두 개의 원래 숫자의 선형 결합으로 표현될 수 있는데, 이는 두 숫자의 합에 각각 정수를 곱한 것이다(예: 21 = 5 × 105 + (-2) × 252).GCD가 항상 이런 식으로 표현될 수 있다는 사실은 베주트의 정체성으로 알려져 있다.(전체 기사...) - Molyneux의 천체 글로브 중 하나는 하클루이트 협회의 1889년 출판된 글러브스의 프런티프에서 나온 것으로 로버트 후스의 라틴 작품 트랙타투스 드 글로브시스(Globis1594)의 영문판 중 하나인 Cœstiall과 Terrestriall이다.
에메리 몰리뉴(/ˈɛməri ˈmɒnoʊ/EM-ər-ee MOL-in-oh; 1598년 6월 사망)는 글로브, 수학 기구, 서던스로 이루어진 잉글리시엘리자벳의 제조사였다.1592년에 처음 출판된 그의 지상구 및 천체구조는 영국에서 최초로 만들어졌으며 영국인에 의해 최초로 만들어졌다.
몰리뉴는 수학자였고 나침반이나 모래시계 같은 수학적 도구를 만드는 사람으로 알려져 있었다.그는 작가 리차드 하클루이트와 수학자 로버트 후스, 에드워드 라이트 등 당대 저명한 인물들을 많이 알게 되었다.그는 또한 탐험가 토마스 캐번디쉬, 프랜시스 드레이크, 월터 롤리, 존 데이비스를 알고 있었다.데이비스는 아마도 자신의 후원자인 런던 상인 윌리엄 샌더슨에게 몰리뉴를 소개했을 것이다. 그는 주로 글로브의 건설에 자금을 조달했다.완성된 글로브는 엘리자베스 1세에게 선물되었다. 더 큰 글로브는 왕족, 귀족, 학원에 의해 획득되었고, 작은 글로브는 선원들과 학생들을 위한 실용적인 항해 보조 도구로 구입되었다.그 글로브는 바다의 습도에 영향을 받지 않을 정도로 처음 만들어진 것이었고, 배에서 일반적으로 쓰이게 되었다. (전체 기사...)
조시아 윌러드 깁스(/ɡɪbz/; 1839년 2월 11일 ~ 1903년 4월 28일)는 물리학, 화학, 수학에 상당한 이론적 공헌을 한 미국의 과학자였다.열역학 응용에 관한 그의 연구는 물리 화학을 엄격한 귀납 과학으로 변화시키는데 도움이 되었다.제임스 서점 맥스웰과 루드비히 볼츠만과 함께 통계역학(그가 만든 용어)을 만들어, 열역학 법칙을 많은 입자로 구성된 물리적 시스템의 가능한 상태의 앙상블의 통계적 속성의 결과로 설명하였다.깁스는 또한 물리적 광학 문제들에 맥스웰의 방정식을 적용하는 일을 했다.수학자로서 그는 현대 벡터 미적분학(동시기에 비슷한 작업을 수행한 영국 과학자 올리버 헤비사이드의 독립)을 발명했다.
1863년 예일은 깁스에게 미국 최초의 공학 박사학위를 수여했다.3년간의 유럽 체류 후, 깁스는 1871년부터 1903년 사망할 때까지 수학 물리학 교수로 있던 예일대에서 나머지 경력을 보냈다.상대적으로 고립된 채 일하면서, 그는 국제적인 명성을 얻은 미국 최초의 이론 과학자가 되었고, 알버트 아인슈타인으로부터 "미국 역사상 가장 위대한 정신"이라는 칭송을 받았다.1901년, 깁스는 당시 국제 과학 단체인 런던 왕립 협회의 코플리 훈장이 "수학적 물리학에 기여한 공로로" 수여한 최고의 영예로 여겨지는 것을 받았다.(전체 기사...)
수학에서는 0.999...(또한 반복 십진법에서 0.9로 표기됨)는 소수점 이후 9s의 연속되지 않는 순서로 구성된 반복 십진법을 의미한다.이 반복적인 십진수는 순서의 모든 소수보다 작은 숫자를 나타낸다(0.9, 0.99, 0.99, ...). 즉, 이 순서의 우월성을 나타낸다.이 숫자는 1과 같다.즉, "0.999..."는 "정확히" 또는 "매우 근접하지만" 1이 아니라 "0.999..."와 "1"은 정확히 같은 숫자를 나타낸다.
직관적인 주장에서부터 수학적으로 엄격한 입증에 이르기까지 이러한 평등을 보여주는 많은 방법들이 있다.사용된 기술은 대상 청중, 배경 가정, 역사적 맥락, 선호되는 실수 개발, 즉 0.999 내의 시스템에 따라 달라진다.일반적으로 정의된다.다른 시스템에서는 0.999...같은 의미, 다른 정의를 가질 수도 있고, 정의되지 않을 수도 있다.(전체 기사...)- 일반 상대성 이론과 아인슈타인의 중력 이론으로도 알려져 있는 일반 상대성 이론은 1915년 알버트 아인슈타인이 발표한 중력의 기하학이며 현대 물리학의 중력에 대한 현재의 설명이다.일반 상대성 이론은 특수상대성이론을 일반화하고 뉴턴의 만유인력의 법칙을 재조명하여 공간과 시간의 기하학적 특성 또는 4차원 시간이라는 중력에 대한 통일된 설명을 제공한다.특히, 스페이스타임의 곡률은 물질과 방사선이 존재하는 모든 것의 에너지와 운동량과 직접적인 관련이 있다.관계는 2차 순서의 부분 미분 방정식의 시스템인 아인슈타인 필드 방정식으로 지정된다.
고전적 중력을 설명하는 뉴턴의 만유인력의 법칙은 고정된 질량분포를 중심으로 거의 평탄한 시간 기하학에 대한 일반상대성이성의 예측으로 볼 수 있다.그러나 일반 상대성에 대한 일부 예측은 고전 물리학에서 뉴턴의 만유인력의 법칙을 벗어난다.이러한 예측은 시간의 흐름, 공간의 기하학, 자유낙하에서의 신체의 운동, 빛의 전파와 관련이 있으며, 중력시간 팽창, 중력렌즈화, 빛의 중력적색편향, 샤피로 시간지연 및 특이점/블랙홀 등이 포함된다.지금까지 일반 상대성 테스트는 모두 이론과 일치한다는 것이 증명되었다.일반 상대성 이론의 시간 의존적 해법은 우주의 역사에 대해 이야기할 수 있게 해주며, 우주론의 현대적 틀을 제공함으로써 빅뱅과 우주 마이크로파 배경 방사선의 발견으로 이어졌다.수많은 대체 이론이 도입되었음에도 불구하고 일반 상대성 이론은 실험 데이터와 일치하는 가장 단순한 이론으로 계속 이어지고 있다.그러나 양자물리학의 법칙과 일반상대성이론의 조정은 여전히 문제점으로 남아 있는데, 양자중력의 자기 일치 이론이 결여되어 있기 때문이다; 그리고 어떻게 중력이 세 가지 비중력 힘인 강, 약, 전자기력과 통일될 수 있는가. (전제 기사...) - 고전역학에서 라플라스-런지-렌츠(LRL) 벡터는 이항성이나 항성 주위를 도는 행성과 같이 한 천문체의 궤도 형태와 방향을 주로 설명하는 데 사용되는 벡터다.뉴턴 중력에 의해 상호작용하는 두 신체에 대해 LRL 벡터는 운동 상수로서, 궤도에서 계산되는 위치에 상관없이 동일하다는 것을 의미하며, 동등하게 LRL 벡터는 보존된다고 한다.보다 일반적으로, LRL 벡터는 두 신체가 그들 사이의 거리의 역제곱에 따라 변하는 중심적인 힘에 의해 상호작용하는 모든 문제에서 보존된다; 그러한 문제를 케플러 문제라고 부른다.
수소 원자는 케플러 문제인데, 이것은 쿨롱의 전기학 법칙에 의해 상호작용하는 두 개의 전하 입자로 구성되어 있기 때문에, 또 다른 역제곱 중심 힘이다.LRL 벡터는 슈뢰딩거 방정식이 개발되기 전 수소원자 스펙트럼의 첫 양자역학적 도출에서 필수적이었다.그러나 오늘날에는 이런 접근법이 거의 사용되지 않는다.(전체 기사...)
유클리드 평면 기하학에서 아폴로니우스의 문제는 한 평면에 주어진 원 3개에 접하는 원들을 구성하는 것이다(그림 1).페르가의 아폴로니우스(기원전 262년–기원전 190년)는 그의 작품 πααφαί(Epaphai, "Tangiencies")에서 이 유명한 문제를 제기하고 해결했다. 이 작품은 소실되었지만 알렉산드리아의 파푸스가 그의 결과를 담은 4세기 AD 보고서는 살아남았다.일반적으로 3개의 주어진 원은 8개의 서로 접하는 원과 접하는 원(그림 2)이 있는데, 이는 주어진 원 3개를 두 개의 하위 세트로 나누는 각 방법에 대한 한 쌍의 해결책이다(카디널리티 3의 한 세트를 두 부분으로 나누는 4가지 방법이 있다).
16세기에 아드리아 판 라멘은 교차하는 하이퍼볼라를 사용하여 문제를 해결했지만, 이 해결책은 직선자와 나침반 구조만을 사용하지 않는다.프랑수아 비에테는 주어진 원 세 개 중 어느 하나라도 0 반지름(점)으로 축소하거나 무한 반지름(선)으로 확장될 수 있다는 제한 사례를 악용해 이런 해법을 찾았다.더 복잡한 경우를 해결하기 위해 더 간단한 제한 사례를 사용하는 비에트의 접근법은 아폴로니우스의 방법을 그럴듯하게 재구성하는 것으로 여겨진다.판 로멘의 방법은 아이작 뉴턴에 의해 단순화되었는데, 그는 아폴로니우스의 문제가 거리의 차이에서 알려진 세 지점까지의 위치를 찾는 것과 동등하다는 것을 보여주었다.이것은 LORAN과 같은 항법 및 위치설정 시스템에 응용된다. (전체 기사...
요하네스 케플러(/ˈkɛplər/; 독일어: [joˈhanss ˈkɛplɐ, -nɛs -](
케플러는 그라츠에 있는 신학교의 수학 교사였는데, 그곳에서 한스 울리히 폰 에겐베르크 왕자의 동료가 되었다.이후 프라하의 천문학자 타이코 브라헤의 조수가 되었고, 결국 루돌프 2세와 그의 두 후계자 마티아스와 페르디난드 2세의 황실 수학자가 되었다.린츠에서도 수학을 가르쳤으며, 월렌슈타인 장군의 조언자였다.
또한 그는 광학 분야에서 기초적인 작업을 했고, 굴절(또는 케플러안) 망원경의 개선된 버전을 발명했으며, 현대판 갈릴레오 갈릴레이의 망원경 발견에 언급되었다.그는 로마에 있는 아카다혈병 데이 린시(Accademia dei Lincei)의 해당 회원이었다. (전체 기사...)- 이 균형척도의 계량 팬은 0개의 물체를 포함하고 있으며, 두 개의 동일한 그룹으로 나뉜다.
수학에서 0은 짝수 또는 0은 짝수다.즉, 그 동등성(정수의 질은 짝수 또는 홀수)은 짝수다.이것은 "짝수"의 정의에 기초하여 쉽게 확인할 수 있다: 2의 정수 배수, 구체적으로는 0 × 2. 그 결과 짝수를 특징짓는 모든 속성을 공유한다. 예를 들어, 0은 홀수로 양쪽에 인접해 있고, 소수 정수는 마지막 숫자와 같은 패리티를 갖는다. 따라서 10은 짝수이므로 0은 짝수일 것이다.y가 짝수인 경우 y + x는 x와 동일한 패리티를 가지며 x와 0 + x는 항상 동일한 패리티를 가진다.
0은 또한 다른 짝수들에 의해 형성된 패턴에도 들어맞는다.even - even = even과 같은 산술의 패리티 규칙은 0이 짝수여야 한다.0은 짝수 정수 집단의 가법적 정체성 요소로서, 다른 자연수마저 재귀적으로 정의되는 시작 사례다.그래프 이론에서 계산 기하학에 이르는 이 반복의 적용은 0의 균등에 의존한다.0은 2로 나눌 수 있을 뿐만 아니라, 2의 모든 힘으로 나눌 수 있는데, 이는 컴퓨터가 사용하는 2진수 체계와 관련이 있다.이런 의미에서 0은 전체 중 "가장 고른" 숫자다.(전체 기사...) - 야콥 에마누엘 핸드만(1753)의 초상화
레온하르트 오일러(/ˈɔlər/OY-lər; 독일어: [ˈɔɔʏl]](
오일러는 역사상 가장 위대한 수학자 중 한 명이고 18세기 중 가장 위대한 수학자 중 한 명이다.피에르 시몬 라플레이스에 기인하는 성명서는 오일러가 수학에 미친 영향력을 표현한다: " 오일러를 읽고, 오일러를 읽고, 그는 우리 모두의 주인이다." 칼 프리드리히 가우스는 " 오일러의 작품에 대한 연구는 수학의 다양한 분야를 위한 최고의 학교로 남을 것이며, 다른 어떤 것도 그것을 대체할 수 없다"고 말했다.오일러는 또한 가장 다작인 것으로 널리 알려져 있다. 그의 850여 권의 출판물은 92쿼토 권으로, (그의 오페라 옴니아 포함) 이 분야의 그 누구보다도 많이 수집되고 있다.그는 성인 생활의 대부분을 러시아의 상트페테르부르크와 당시 프로이센의 수도 베를린에서 보냈다.(전체 기사...)
악덕인은 위험과 불확실성의 측정과 관리를 다루는 비즈니스 전문가다.해당 분야의 명칭은 보험수리적 과학이다.이러한 위험은 대차대조표 양쪽에 영향을 미칠 수 있으며 자산관리, 부채관리 및 가치평가 능력을 요구한다.보험계약자는 금융보안 시스템의 복잡성, 수학 및 메커니즘에 초점을 맞춰 금융보안 시스템의 평가를 제공한다.
보험의 개념은 고대로 거슬러 올라가지만, 위험을 과학적으로 측정하고 완화하는데 필요한 개념은 17세기 확률과 연금에 대한 연구에 그 기원을 두고 있다.21세기의 보험업자들은 위험을 통제하는 프로그램을 설계하고 관리하기 위해 분석 기술, 사업 지식, 그리고 인간 행동과 정보 시스템에 대한 이해를 요구한다.법학자가 되기 위해 필요한 실제 단계는 대개 나라마다 다르지만, 거의 모든 과정이 엄격한 학교 교육이나 시험 구조를 공유하며 완료하는 데 많은 시간이 걸린다.(전체 기사...)
기사의 투어는 기사라고 불리는 작품이 다른 빈 체스판의 각 광장을 정확히 한 번, 합법적인 움직임만을 사용하여 방문하게 되는 수학적인 체스 문제다.그래프 이론에서 보다 일반적인 해밀턴 경로 문제의 특수한 경우다.(밀접하게 연관되어 있는 비 해밀턴적 문제는 가장 길지 않은 기사의 경로 문제)기사가 합법적으로 출발 광장으로 이동할 수 있는 광장(그 곳에서 끝없는 순환을 형성하여)에서 끝나면 투어는 폐쇄라고 하며, 그렇지 않으면 개방된다.이 애니메이션에 표시된 투어는 열려 있다(완료된 투어의 정적 이미지 참조).표준 8 × 8 기판에는 26,534,728,821,064개의 가능한 폐쇄 투어 및 39,183,656,341,341,959,810개의 오픈 투어(회전, 반사 또는 역방향으로 동일한 투어 포함)가 있다.기사의 여행 문제에 대한 가장 초기 알려진 해결책은 9세기까지 거슬러 올라갔지만, 기사의 여행을 완성하기 위한 첫 번째 일반적인 절차는 1823년에 처음 묘사된 경고도르프의 규칙이었다.이 기사의 투어는 1770년부터 1854년까지 오토매틱으로 전시된 가짜 체스 플레이 기계인 투르크에 의해 해결된 많은 체스 퍼즐 중 하나였으며, 1820년대 초 정교한 장난으로 노출되었다.1950년대에 진정한 체스 게임 오토매턴(즉, 컴퓨터 프로그램)이 등장했고, 1988년까지 그랜드 마스터와의 경기에서 승리할 만큼 충분히 발전했다; 1997년에 딥 블루는 표준 토너먼트 타임제어에 따라 세계 챔피언(Garry Kasparov)을 물리친 최초의 컴퓨터 시스템이 되었다.이러한 진전에도 불구하고 체스가 컴퓨터 문제(체스 시합에서 절대 질 수 없는 알고리즘이 개발됨을 의미)로 '해결'될 수 있을지에 대해서는 여전히 논쟁이 있다.제르멜로의 정리대로라면 그런 알고리즘이 실제로 존재한다.
