A Wikipédiából, a szabad enciklopédiából
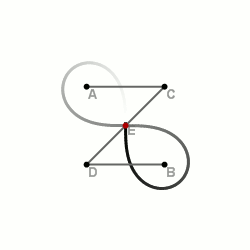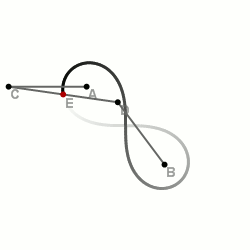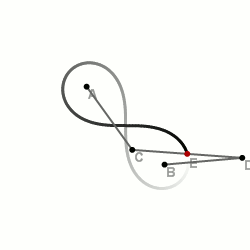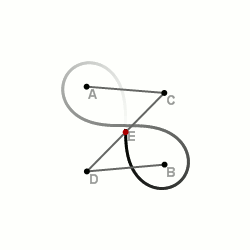
A lemniszkáta. Lemniszkáta szerkesztése. Az ábrán látható háromtagú csuklós mechanizmus középső rúdjának felezőpontja a mechanizmus mozgatása során lemniszkátát ír le. A lemniszkáta egy speciális Cassini-görbe . A Cassini-görbék a sík olyan pontjainak mértani helyei, melyekre igaz, hogy két adott ponttól való távolságának szorzata állandó. Azt a Cassini-görbét nevezzük lemniszkátának, amelyiken rajta van a két adott pontot összekötő szakasz felezőpontja. A lemniszkáta egy 8 (vagy
∞
{\displaystyle \infty }
Az ábra jelöléseivel derékszögű koordináta-rendszerben:
(
x
2
+
y
2
)
2
−
2
c
2
(
x
2
−
y
2
)
=
0
{\displaystyle {\left(x^{2}+y^{2}\right)}^{2}-2c^{2}\left(x^{2}-y^{2}\right)=0}
Polárkoordinátákkal:
ρ
=
c
2
cos
2
φ
{\displaystyle \rho =c{\sqrt {2\cos {2\varphi }}}}
ahol
φ
∈
⟨
−
π
4
,
π
4
⟩
∪
⟨
3
π
4
,
5
π
4
⟩
{\displaystyle \varphi \in \langle -{\frac {\pi }{4}},{\frac {\pi }{4}}\rangle \cup \langle {\frac {3\pi }{4}},{\frac {5\pi }{4}}\rangle }
Paraméteres egyenletrendszere:
x
=
c
t
2
1
+
t
2
1
+
t
4
{\displaystyle x=ct{\sqrt {2}}{\frac {1+t^{2}}{1+t^{4}}}}
y
=
c
t
2
1
−
t
2
1
+
t
4
{\displaystyle y=ct{\sqrt {2}}{\frac {1-t^{2}}{1+t^{4}}}}
ahol
t
∈
R
{\displaystyle t\in \mathbb {R} }
A görbe polárkoordinátákkal megadott egyenleteihez tartozó görbületi sugár:
R
=
2
c
2
3
ρ
=
c
1
+
t
4
3
|
t
|
{\displaystyle R={\frac {2c^{2}}{3\rho }}={\frac {c{\sqrt {1+t^{4}}}}{3|t|}}}
feltéve, hogy
ρ
≠
0
{\displaystyle \rho \neq 0}
t
≠
0
{\displaystyle t\neq 0}
T
=
c
2
{\displaystyle T=c^{2}\,}
Kerülete:
k
≈
2
c
⋅
1
,
8541
{\displaystyle k\approx 2c\cdot 1,8541\,}
Ha az
x
2
−
y
2
=
c
2
{\displaystyle x^{2}-y^{2}=c^{2}\,}
hiperbolát az
x
2
+
y
2
=
c
2
{\displaystyle x^{2}+y^{2}=c^{2}\,}
körön tükrözzük, lemniszkátát kapunk.
J. N. Bronstein - K. A. Szemengyajev: Matematikai zsebkönyv . Műszaki könyvkiadó, Budapest, 1987. ISBN 963-10-53091
Pattantyús Gépész- és Villamosmérnökök Kézikönyve 2. kötet. Műszaki Könyvkiadó, Budapest, 1961.