Silogismo
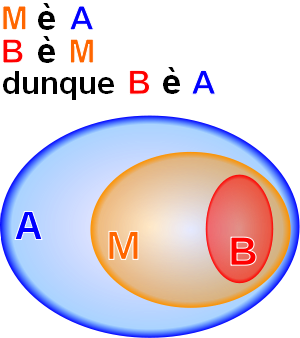
se M estas A
kaj B estas M,
tiam B estos ankaŭ A.
Por konkretigi la ekzemplon: M estu la aro da dolĉaĵoj; B, la aro da tortoj; kaj A, la aro da nutraĵoj:
ĉiuj dolĉaĵoj estas nutraĵoj
kaj ĉiuj tortoj estas dolĉaĵoj,
sekve ĉiuj tortoj estas nutraĵoj.
Klarigo
[redakti | redakti fonton]Silogismo (de la greka συλλογισμός, syllogismòs, formita el σύν, syn, "kune", kaj λογισμός, logismòs, "konkludo, inferenco": tial, "kunĉenita rezonado") estas tipo de pruva rezonado unuafoje sisteme prezentita de Aristotelo[1], kiu startinte el tri tipoj de termoj: maĵora (kiu funkcias kiel predikato en la konkludo), meza kaj minora (kiu en la konkludo funkcias kiel subjekto) klasifikitaj surbaze de la rilato “entenanto-entenato”, atingas konkludon kunigante la suprediritajn termojn tra mallongaj formuladoj (premisoj).

La formo de silogismo plej komuna estas la kategoria silogismo (kutime per silogismo oni celas la kategorian silogismon).
La propozicioj kiu konsistigas kategorian silogismon povas esti:
- universalaj pozitivaj ("Ĉiuj A estas B"),
- universalaj negativaj ("Neniu A estas B"),
- apartaj pozitivaj ("Iuj A estas B"),
- apartaj negativaj ("Iuj A ne estas B").
La pozicio de la termo meza en la du premisoj determinas la figuron de la silogismo; da ili Aristotelo klasifikis tri, sed la skolastikuloj aldonis la kvaran. La formo de la propozicioj entenataj en silogismo determinas ĝian moduson; skolastika logiko klasifikis la silogismajn modusojn uzate la unuan aŭ la duan vokalon (respektive se universala aŭ parta) de la Latinaj verboj affirmo (= mi asertas) kaj nego (= mi negas).
Ekzemple:
- (maĵora premiso) Ĉiuj homoj estas mortemaj
- (minora – meza – premiso) Ĉiuj grekoj estas homoj
- (konkludo) Do, ĉiuj grekoj estas mortemaj
En la supra ekzemplo, homo, mortemaj kaj grekoj estas termoj (respektive maĵora, meza, minora).
Dua pli signifa ekzemplo povas esti:
- (maĵora premiso) Ĉiuj besto estas mortemaj
- (minora – meza – premiso) Ĉiu homo estas besto
- (konkludo) Do, ĉiu homo estas mortema
La meza termo estas la elemento danke al kiu okazas la unuigo, ĝi funkcias kiel kunligilo inter la du aliaj; tio ĉar la meza termo (besto) unuflanke estas inkluzivita en la maĵora termino (mortema) kaj aliflanke inkluzivas en si la minoran terminon (homo).
Silogismon oni taksas valida se ĝi estas laŭlogike valida. La valido de silogismo ne dependas de la vero de la asertoj kiuj ĝin komponas. Tiel ke silogismo:
- ĉiu besto flugas
- la azeno estas besto
- do la azeno flugas
estas valida ankaŭ se la frazoj, kiuj ĝin konsistigas ne estas veraj. Metodo, aŭ raspa difino, kiu ofte uzatas, estas diri: "silogismo estas valida se ĉiuj samformaj silogismoj kiu entenas propoziciojn verajn konkludas ĝuste". Tiu metodo tamen ne havas prilogikan dignecon, ĉar, spite de ĝia funkcieco, utiligas neniun logikon. Silogismo aranĝita per propozicioj ĉiuj veraj povas esti rekonata nevalida ankaŭ se vera.
Ekzemple:
- La dioj estas senmortemaj
- La homoj ne estas dioj
- Do, la homoj ne estas senmortemaj.
Tia silogismo lamas per manko de logiko ankaŭ se ĉiuj ĝiaj propozicioj estas veraj, kaj tion eblas kompreni simple per rezonado: la dioj estas senmortemaj (frazo vera) diras ke dioj apartenas al la kategorio de la senmortuloj. Pri tiu kategorio ni scias nenion kaj nenio diras, ke ĝi estas konsistas nur el dioj. La homoj ne estas dioj (vera), sed tio ne ekskludas la eblon ke ili povus esti senmortemaj malgraŭ ilia restado en la kategorio de nedioj. La valido de silogismo estas inrinseka karakterizo de la logiko kiu en ĝi estas kunnatura. Ne necesas refoje fari ĝis kiam evidentiĝas ke el du propozicioj veraj elfluas unu malvera, por montri la nevalidecon, sed sufiĉas studi atente la aferon kaj evidentigi la nelogitecon, kiel montrite en la antaŭa ekzemplo.
La dinamikoj de la logiko de silogismoj estas akordigeblaj kun tiuj de la kondiĉoj Necesaj kaj Sufiĉaj, gvidosignoj de la moderna logiko. Se unu de la premisoj estas malvera, la konkludo estas necese malvera; male, la vero de ambaŭ ne kuntrenas ke la konkludo estas vera. Se, tamen, la silogismo estas valida, el du premisoj veraj elvenas konkludo vera. Se ambaŭ estas malveraj kutime la konkludo estas malvera, sed foje povas esti hazarde vera (ekz: ĉiuj homoj estas birdoj, ĉiuj birdoj estas mamuloj, do ĉiuj homoj estas mamuloj)
Kombina kalkulo
[redakti | redakti fonton]Eta resuma aludo al kombina kalkulo por determini la eblaj silogismoj. La tipoj de silogismoj eblaj estas, laŭ analizantoj de la homa lingvaĵo, 256: estas, fakte, tri sendependaj propozicioj, ĉiu el kiuj povas ricevi kvar malsamajn formojn por totalo de 4×4×4 kombinaĵoj (x4 figuroj). La figuro estas determinita de la pozicio de la meza termino, kiu estas koncepto ĉeesta en ambaŭ premisoj. La modusoj validaj tamen estas nur 19, nome 4 modusoj (Barbara, Celarent, Darii, Ferio) perfektaj (kiujn Aristotelo difinis memevidentaj) de la silogismo de la unua figuro kaj aliaj 15 pri kiuj eblas pruvi la validecon pere de la tri reguloj de konvertago aŭ la reductio ad impossibile (redukto al la neebleco).
La ĉi-suba teorio de la Distribuado de terminoj ebligas decidi ĉu silogismo estas valida.
| 1 |  Barbara |
 Barbari |
 Darii |
 Ferio |
 Celaront |
 Celarent |
||||||||
| 2 |  Festino |
 Cesaro |
 Cesare |
 Camestres |
 Camestros |
 Baroco |
||||||||
| 3 |  Darapti |
 Datisi |
 Disamis |
 Felapton |
 Ferison |
 Bocardo | ||||||||
| 4 |  Bamalip |
 Dimatis |
 Fesapo |
 Fresison |
 Calemes |
 Calemos |
Notoj
[redakti | redakti fonton]- ↑ Luis Guerrero Martínez Lògica: el raonament deductiu formal , p. 165, Publicacions Creu OSA, 1991 ISBN 978-968-20-0272-4
Bibliografio
[redakti | redakti fonton]- Miguel Candel Sanmartín, Metafísica de rodalies, p. 55, Editorial Montesinos, 2004 ISBN 978-84-95776-85-3
- Clark, J. T., Conventional Logic And Modern Logic.1952
Vidu ankaŭ
[redakti | redakti fonton]- Inferenco
- Listo de reguloj de inferenco
- Silogismo alternativa
- Silogismo hipoteza
- Modus ponens
- Modus tollens
- Logika valideco
- Aristotela logiko
- Filozofio
- Taŭtologio
- Venn-a diagramo
Aliaj projektoj
[redakti | redakti fonton]- Komuna ofertas aliajn reprezentaĵojn de la modusoj de silogismo
- En Itallingva Wikizionario [1] troviĝas