쌍곡면에서의 균일한 타일링
Uniform tilings in hyperbolic plane| 구면 | 유클리드 | 쌍곡선 | |||
|---|---|---|---|---|---|
 {5,3} 5.5.5 |  {6,3} 6.6.6 |  {7,3} 7.7.7 |  {∞,3} ∞.∞.∞ | ||
| 정오각형, 육각형 및 칠각형 및 편평면을 사용하는 구체의 정타일링 {p,q}, 유클리드 평면 및 쌍곡면. | |||||
 t{5,3} 10.10.3 |  t{6,3} 12.12.3 |  t{7,3} 14.14.3 |  t{buffic,3} ∞.∞.3 | ||
| 잘린 타일링은 정규 {p,q}의 2p.2p.q 꼭지점 숫자를 가집니다. | |||||
 r{5,3} 3.5.3.5 |  r{6,3} 3.6.3.6 |  r{7,3} 3.7.3.7 |  r{syslog,3} 3.∞.3.∞ | ||
| 준규격 타일링은 정규 타일링과 유사하지만 각 정점을 중심으로 두 가지 유형의 규칙 폴리곤을 번갈아 사용합니다. | |||||
 rr{5,3} 3.4.5.4 |  rr{6,3} 3.4.6.4 |  rr{7,3} 3.4.7.4 |  rr{param,3} 3.4.∞.4 | ||
| 반규칙 타일링에는 둘 이상의 유형의 정규 폴리곤이 있습니다. | |||||
 tr{5,3} 4.6.10 |  tr{6,3} 4.6.12 | 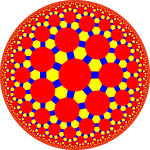 tr{7,3} 4.6.14 | 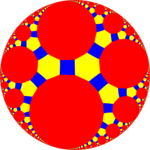 tr {syslog,3} 4.6.∞ | ||
| 옴니트런티드 타일링에는 세 개 이상의 짝수 면 정규 폴리곤이 있습니다. | |||||
| 대칭 | 삼각 이면체 대칭 | 사면체 | 팔면체 | 이십면체 | p6m 대칭 | [3,7] 대칭 | [3,8] 대칭 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 솔리드 시작 작동 | 기호. {p,q} | 삼각 호소면체 {2,3}  | 삼각 이면체 {3,2}  | 사면체 {3,3}  | 큐브 {4,3}  | 팔면체 {3,4}  | 십이면체 {5,3}  | 이십면체 {3,5}  | 육각형 타일링 {6,3}  | 삼각 타일링 {3,6}  | 칠각형 타일링 {7,3}  | 7차 삼각 타일링 {3,7}  | 팔각형 타일링 {8,3}  | 8차 삼각 타일링 {3,8}  |
| 잘라내기(t) | t{p,q} | 삼각 프리즘 | 잘린 삼각 이면체 ('에지'의 절반은 퇴화 디곤 면으로 카운트됩니다.나머지 절반은 정상 가장자리입니다.) | 깎은 사면체 | 잘린 입방체 | 잘린 팔면체 | 잘린 12면체 | 깎은 20면체 | 잘린 육각형 타일링 | 잘린 삼각형 타일링 | 잘린 7각형 타일링 | 잘린 순서-7 삼각형 타일링 | 잘린 팔각형 타일링 | 잘린 순서-8 삼각형 타일링 |
| 수정(r) Ambo(a) | r{p,q} | 삼면체(모든 "edge"는 퇴화 디곤 면으로 카운트됩니다). | 사면체 | 육팔면체 | 이십이면체 | 삼육각 타일링 | 삼육각 타일링 | 삼팔각형 타일링 | ||||||
| 비트런케이션 (2t) 듀얼키(dk) | 2t{p,q} | 잘린 삼각 이면체('에지'의 절반은 퇴화 디곤 면으로 카운트됩니다.나머지 절반은 정상 가장자리입니다.) | 삼각 프리즘 | 깎은 사면체 | 잘린 팔면체 | 잘린 입방체 | icosahedron는 잘리 | 잘려진 12면체 | 잘려진 타일 붙이기 삼각형 | 육방 tiling들의 길이를 줄였다 | order-7 삼각 타일 Truncated | 7각형의. tiling Truncated | order-8 삼각 타일 Truncated | Truncatedtiling 팔모의 |
| Birectification(2r) 듀얼(d) | 2r{p,q} | dihedron 삼각 {3,2} | 삼각 hosohedron {2,3} | 4면체 | 8면체 | 큐브 | 20면체 | 12면체 | 삼각 타일링 | 육각형 타일링 | 7차 삼각 타일링 | 칠각형 타일링 | 8차 삼각 타일링 | 팔각형 타일링 |
| 칸테레이션(rr) 확장(e) | rr{p,q} | 삼각 프리즘(각 사각형 쌍 사이의 "엣지"는 퇴화된 사각형 면으로 간주됩니다.다른 에지(트리거와 사각형 사이의 에지)는 정규 에지입니다. | 마름비테트라면체 | 마름모꼴 팔면체 | 마름모꼴 십이면체  | 로밋리헥사각형 타일링 | 롬비트리헵타일링  | 롬빗리옥타일링  | ||||||
| 스너브 수정 완료(sr) 스누브 | sr{p,q} | 삼각 반체제 (3개의 황색 "에지"는 정점을 공유하지 않으며 퇴화 디곤 면으로 간주됩니다.다른 엣지는 일반 엣지입니다). | 스너브 사면체 | 스너브 육팔면체 | 스누브 이십이면체 | 스눕 삼육각 타일 | 스눕 삼칠각 타일링 | 스눕 삼팔각형 타일링 | ||||||
| 캔티트런케이션(tr) 베벨(b) | tr{p,q} | 육각 프리즘 | 절삭 사면체 | 깎은 정육면체 | 깎은 이십이면체 | 잘린 삼육각 타일링 | 잘린 삼육각 타일링 | 잘린 삼팔각형 타일링 | ||||||
쌍곡선 기하학에서 균일한 쌍곡선 타일링(또는 규칙, 준규칙 또는 반규칙 쌍곡선 타일링)은 정다각형들을 면으로 가지며 정점-추이적이다(정점에서의 추이, 즉 정점을 다른 정점에 매핑하는 등각도가 있다).따라서 모든 정점은 일치하며 타일링은 높은 회전 및 변환 대칭을 가집니다.
균일한 타일링은 각 정점 주변의 폴리곤의 변 수를 나타내는 일련의 숫자인 정점 구성으로 식별할 수 있습니다.예를 들어, 7.7.7은 각 정점 주위에 3개의 헵타곤이 있는 7각형 타일을 나타냅니다.또한 모든 폴리곤의 크기가 같기 때문에 규칙적이기 때문에 슐래플리 기호 {7,3}도 지정할 수 있습니다.
균일한 타일링은 정규(면 전이 및 가장자리 전이인 경우), 준정규(면 전이이지만 면 전이 아닌 경우) 또는 반정규(면 전이인 경우)일 수 있습니다.직각 삼각형(p q 2)의 경우 슐레플리 기호 {p,q} 및 {q,p}으로 표시되는 두 개의 규칙 타일링이 있습니다.