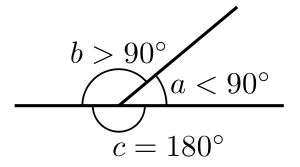각
Angle이 기사는 검증을 위해 추가적인 인용이 필요합니다. 찾기 :– · · (2022년 7월)(본 방법 및 |

유클리드 기하학에서 각도는 각도의 변이라고 불리는 두 개의 광선이 각도의 꼭짓점이라고 불리는 공통된 끝점을 공유하여 형성한 도형입니다.[1]두 개의 광선에 의해 형성된 각도는 광선을 포함하는 평면에 놓여 있기 때문에 평면 각도라고도 알려져 있습니다.각도들은 또한 두 평면들의 교차에 의해 형성됩니다; 이것들은 이면체 각도들이라고 불립니다.두 개의 교차하는 곡선이 교차점에서 각 곡선에 접하는 광선의 각도인 각도를 정의할 수도 있습니다.
각도의 크기를 각도 측정 또는 간단히 "각도"라고 합니다.회전 각도는 원호 길이와 반지름의 비율로 통상적으로 정의되는 측도이며, 음수일 수 있습니다.기하학적 각도의 경우, 호는 꼭지점의 중앙에 위치하고 측면으로 구분됩니다.회전의 경우 호는 회전의 중심에 있고 다른 점으로 구분되며 이미지는 회전으로 구분됩니다.
역사와 어원
각(angle)이라는 단어는 "귀퉁이"를 의미하는 라틴어 angulus에서 유래되었습니다. 동족어로는 "구부리고 구부러진"을 의미하는 그리스어 ἀγκύλος (angkyl ο)와 영어 단어 "ankle"을 포함합니다.둘 다 인도유럽조어의 어근 *ank-와 연결되어 있는데, "굽혀지다" 또는 "절"을 의미합니다.[2]
유클리드는 평면각을 평면상에서 서로 마주치고 서로에 대해 똑바로 눕지 않는 두 선의 서로에 대한 기울기로 정의합니다.신플라톤 형이상학자 프로클로스에 따르면, 각도는 질, 양, 또는 관계 중 하나여야 합니다.첫 번째 개념인 각도를 품질로 본 로도스의 에우데무스는 각도를 직선으로부터의 편차로 간주했고, 두 번째 각도를 품질로 본 안티오키아의 카르푸스는 교차하는 선 사이의 간격이나 공간으로 간주했습니다. 유클리드는 세 번째 각도를 관계로 채택했습니다.[3]
식별각
수학적 표현에서는 그리스 문자를 사용하는 것이 일반적입니다 (α,β,γ,θ,φ, 어떤 각도의 크기를 나타내는 변수(다른 의미와의 혼동을 피하기 위해 기호 π는 일반적으로 이러한 용도로 사용되지 않음).소문자 로마자(a, b, c, ...)도 사용됩니다.이것이 혼동되지 않는 상황에서, 각은 꼭짓점을 나타내는 대문자 로마자로 표시될 수 있습니다.예는 이 기사의 그림을 참조하십시오.
세 개의 정의점은 기하학적 도형에서 각도를 식별할 수도 있습니다.예를 들어, 광선 AB와 AC(즉, 점 A에서 점 B와 C까지의 반선)가 이루는 꼭지점 A와의 각도는 ∠BAC 또는 혼동의 우려가 없는 경우에는 각도를 한 꼭짓점 단독으로 지칭할 수 있습니다(이 경우 "각도 A").
잠재적으로 ∠BAC로 표시되는 각도는 A를 기준으로 B에서 C까지의 시계 방향 각도, A를 기준으로 B에서 C까지의 시계 방향 각도, A를 기준으로 C에서 B까지의 시계 방향 각도, A를 기준으로 C에서 B까지의 시계 방향 각도, A를 기준으로 C에서 B까지의 시계 방향 각도 중 하나를 나타낼 수 있습니다(§ 부호 있는 각도 참조).그러나 많은 기하학적 상황에서 180도 이하의 양각을 의미하는 것은 문맥상 명백하며, 이러한 경우에는 모호함이 발생하지 않습니다.그렇지 않으면 모호성을 방지하기 위해 특정 규칙을 채택할 수 있습니다. 예를 들어, ∠BAC는 항상 A에 대해 B에서 C까지의 시계 반대(양)각을 참조하고 ∠CAB는 A에 대해 C에서 B까지의 시계 반대(양)각을 참조합니다.
각의 종류
개개각
측정값이 항상 음수가 아닌 각도에 대한 일반적인 용어가 있습니다( § 부호화된 각도 참조).
- 0°와 같거나 회전하지 않은 각도를 영각이라고 합니다.[5]
- 직각보다 작은 각도(90°미만)예각("sharp", "acute"이라는 뜻)이라고 합니다.
- 각도는 다음과 같습니다.1/4회전(90° 또는 π/2 라디안)을 직각이라고 합니다.직각을 이루는 두 개의 선을 정규선, 직교선 또는 수직선이라고 합니다.[7]
- 직각보다 크고 직각보다 작은 각도(90°~180° 사이)둔각("obt 사용", "blunt"을 의미함)이라고 합니다.
- 1/2회전(180° 또는 π 라디안)과 같은 각도를 직선 각도라고 합니다.
- 직선 각도보다 크지만 1회전 미만인 각도(180°~360° 사이)반사각이라고 합니다.
- 1회전(360° 또는 π 라디안)과 같은 각도를 만각, 완전각, 둥근각 또는 원근각이라고 합니다.
- 직각의 배수가 아닌 각도를 경사각이라고 합니다.
이름, 간격 및 측정 단위는 아래 표에 나와 있습니다.
| 이름. | 영각 | 예각 | 직각 | 둔각 | 직각 | 반사각 | 근막의 | |||
| 구성 단위 | 간격 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 돌다 | 0턴 | (0, 1/4) 회전 | 1/4회전 | (1/4, 1/2) 회전 | 1/2회전 | (1/2, 1) 회전 | 1회전 | |||
| 라디안의 | 0 rad | (0, 1/2π) rad | 래드 1/2π | (1/2π, π) rad | π 래드 | (π, π) rad | 래드 2 π | |||
| 도 | 0° | (0, 90)° | 90° | (90, 180)° | 180° | (180, 360)° | 360° | |||
| 곤 | 0g | (0, 100)g | 100g | (100, 200)g | 200g | (200, 400)g | 400g | |||
세로 및인접 각도 쌍

두 직선이 한 점에서 교차하면 네 개의 각도가 형성됩니다.쌍방향으로, 이 각도들은 서로 상대적인 위치에 따라 이름이 붙여집니다.
- 서로 반대되는 한 쌍의 각도는 "X" 같은 모양을 이루는 두 개의 교차하는 직선에 의해 형성되며 수직각 또는 반대각 또는 수직 반대각이라고 불립니다.그것들은 vert. opp. ∠라고 줄여집니다.
수직으로 반대각이 같은 것을 수직각 정리라고 합니다.로도스의 에우데무스는 그 증거를 밀레토스의 탈레스에게 돌렸습니다.[9][10]명제는 한 쌍의 수직각이 모두 인접한 두 각도에 보충적이기 때문에 수직각의 측정이 동일하다는 것을 보여주었습니다.역사적 기록에 따르면,[10] 탈레스가 이집트를 방문했을 때, 그는 이집트인들이 서로 교차하는 두 개의 선을 그릴 때마다, 그것들이 동등한지 확인하기 위해 수직 각도를 측정하는 것을 관찰했습니다.탈레스는 다음과 같은 일반적인 개념을 받아들인다면 모든 수직각이 동일하다는 것을 증명할 수 있다고 결론지었습니다.
- 모든 직선 각도는 같습니다.
- 등식에 더해진 등식은 등식입니다.
- 등식에서 뺀 등식은 등식입니다.
두 개의 인접한 각도가 직선을 형성할 때는 보조 각도입니다.따라서 각도 A의 측정값이 x와 같다고 가정하면 각도 C의 측정값은 180° - x가 됩니다. 마찬가지로 각도 D의 측정값도 180° - x가 됩니다. 각도 C와 각도 D의 측정값은 모두 180° - x와 같고 합동입니다.각도 B는 두 각도 C와 D에 보충적이기 때문에, 각도 B의 측정값을 결정하는 데 이들 각도 측정값 중 하나를 사용할 수 있습니다.각도 C 또는 각도 D의 측정값을 사용하면 각도 B의 측정값이 180° - (180° - x) = 180° - 180° + x = x임을 알 수 있습니다.따라서 각도 A와 각도 B 모두 측정값이 x와 같고 측정값이 같습니다.
각도 A와 B가 인접해 있습니다. - 인접 각도, 종종 adj로 축약됩니다. ∠은 공통된 꼭짓점과 모서리를 공유하지만 내부 점은 공유하지 않는 각도입니다.다시 말해, 그들은 나란히 또는 인접한 각도이며, "팔"을 공유합니다.직각, 직선각 또는 만각에 합을 맞춘 인접 각도는 특수하며 각각 상보, 보각, 보각이라고 합니다(아래 § 각도 쌍 결합 참조).
가로선은 한 쌍의 (종종 평행한) 선과 교차하는 선으로, 서로 다른 내각, 대응하는 내각, 내각 및 외부각과 연관됩니다.[11]
각도 쌍 결합
세 개의 특별한 각도 쌍은 각도의 합을 포함합니다.

- 상보각은 측정값이 1개의 직각(1/4회전, 90° 또는 π/2 라디안)에 해당하는 각도 쌍입니다.두 상보각이 인접한 경우 비공유 변은 직각을 형성합니다.유클리드 기하학에서 직각삼각형의 두 예각은 서로 상보적인데, 삼각형의 내각의 합이 180도이고 직각이 90도를 차지하기 때문입니다.
형용사 보어는 라틴어 보어에서 따온 것으로, 동사 보어인 "채우다"와 연관되어 있습니다.예각은 보체에 의해 "채움"되어 직각을 형성합니다.
각도와 직각 사이의 차이를 각도의 상보라고 합니다.[13]
각도 A와 B가 상보이면 다음 관계가 성립합니다.
(각의 접선은 상보의 공접선과 같고, 초는 상보의 초접선과 같습니다.)
일부 삼각형 비율의 이름에서 접두사 "co-"는 "complementary"라는 단어를 나타냅니다.
각들은a그리고.b보조각입니다. - 직선각과 합이 되는 두 개의 각도(1/2회전, 180° 또는 π 라디안)를 보조각이라고 합니다.
두 보조각이 인접해 있으면(즉, 공통 꼭짓점을 가지고 한 변만 공유), 비공유 변은 직선을 형성합니다.이러한 각도를 선형 각도 쌍이라고 합니다.[15]그러나 보조각은 같은 선에 있을 필요가 없으며 공간에서 분리될 수 있습니다.예를 들어, 평행사변형의 인접한 각도는 보조이고, 순환 사각형(꼭짓점이 모두 하나의 원 위에 있는 것)의 반대 각도는 보조입니다.
점 P가 중심이 O인 원의 외부에 있고, 점 T 및 Q에서 P의 접선이 원에 닿으면 ∠TPQ 및 ∠TOQ는 보충적입니다.
보조각의 사인은 같습니다.코사인과 접선(정의되지 않은 경우)은 크기가 같지만 부호가 반대입니다.
유클리드 기하학에서, 삼각형의 내각의 합은 직선각이기 때문에 삼각형의 두 내각의 합은 세 번째 내각에 보충됩니다.
각도 AOB와 COD는 완전한 각도를 형성하기 때문에 켤레입니다.진도를 고려하면 45° + 315° = 360°입니다. - 완전한 각도(1회전, 360도 또는 2 π 라디안)에 해당하는 두 개의 각도를 외각 또는 공액각이라고 합니다.
각도와 완전한 각도 사이의 차이를 각도의 수식 또는 공액이라고 합니다.

- 단순 다각형의 일부인 각도는 단순 다각형의 안쪽에 있는 경우 내부 각도라고 합니다.단순 오목 다각형은 적어도 하나의 내부 각도, 즉 반사 각도를 갖습니다. 유클리드 기하학에서 삼각형의 내각 측정값은 π 라디안, 180° 또는 1/2회전에 더해지며, 단순 볼록 사각형의 내각 측정값은 π 라디안, 360° 또는 1회전에 더해집니다.일반적으로, n개의 변을 갖는 단순 볼록 다각형의 내각의 측정값은 (n - 2) π 라디안 또는 (n - 2)180도, (n - 2)2개의 직각 또는 (n - 2)1/2회전에 더해집니다.
- 내부 각도의 보충은 외부 각도(external angle)라고 합니다. 즉, 내부 각도와 외부 각도는 선형 각도 쌍을 형성합니다.다각형의 각 꼭짓점에는 두 개의 외각이 있으며, 각 외각은 꼭짓점에서 만나는 다각형의 두 변 중 하나를 확장하여 결정됩니다. 이 두 각도는 수직이므로 동일합니다.외각은 다각형을 추적하기 위해 꼭지점에서 회전해야 하는 양을 측정합니다.[16]해당 내부 각도가 반사각일 경우 외부 각도는 음으로 간주해야 합니다.단순하지 않은 다각형에서도 외부 각도를 정의할 수 있습니다.그러나 평면(또는 표면)의 방향을 선택하여 외부 각도 측정의 부호를 결정해야 합니다.유클리드 기하학에서, 두 개의 외각 중 하나만 각 꼭짓점에서 가정할 경우 단순 볼록 다각형의 외각의 합은 한 바퀴(360°)가 됩니다.여기서의 외각은 보조 외각이라고 할 수 있습니다.일반 다각형을 그릴 때 로고 터틀 프로그램에서 일반적으로 외각을 사용합니다.
- 삼각형에서 두 외부 각도의 이등분선과 다른 내부 각도의 이등분선은 동시에 있습니다(단일 지점에서 만납니다).[17]: 149
- 삼각형에서, 세 개의 교점들, 즉 각각이 확장된 변을 갖는 외부 각도 이등분선은 공선입니다.[17]: p. 149
- 삼각형에서, 내부 각도 이등분선과 반대쪽 면 사이에 있는 두 개의 교점과 다른 외부 각도 이등분선과 확장된 반대쪽 면 사이에 있는 세 개의 교점은 공선입니다.[17]: 149
- 일부 저자는 단순 다각형의 외각이라는 이름을 사용하여 내각의 외각(보충이 아닌!)을 설명합니다.[18]이는 위의 용법과 상충됩니다.
- 두 평면 사이의 각도(예: 다면체의 인접한 두 면)를 다면체 각도라고 합니다.[13]평면에 수직인 두 선 사이의 예각으로 정의할 수 있습니다.
- 평면과 교차하는 직선 사이의 각도는 교차하는 직선과 교차점을 통과하는 직선 사이의 각도를 뺀 90도입니다.
측정각
기하학적 각도의 크기는 일반적으로 광선 중 하나를 다른 광선으로 매핑하는 가장 작은 회전의 크기로 특징지어집니다.같은 크기의 각도들은 측정값이 같거나 같다고 합니다.
원 위의 점을 식별하거나 기준 방향과 관련된 2차원에서 물체의 방향을 설명하는 것과 같은 일부 맥락에서 전체 회전의 정확한 배수만큼 다른 각도는 효과적으로 동등합니다.나선형 곡선 상의 점을 식별하거나 기준 방향에 대한 2차원에서의 객체의 누적 회전을 설명하는 것과 같은 다른 맥락에서는 만회전의 0이 아닌 배수만큼 다른 각도는 동일하지 않습니다.

각도를 측정하는 방법θ, 예를 들어, 한 쌍의 나침반으로 각도의 꼭지점에 중심을 둔 원호가 그려집니다.길이의 비율s반지름만큼 호의r원의 개수는 각도에 있는 라디안의 개수입니다.[19]
다른 각도 단위로 표현되는 각도는 각도에 k/2 π 형태의 적합한 변환 상수를 곱하여 구할 수 있습니다. 여기서 k는 선택된 단위로 표현되는 완전한 회전의 척도입니다(예: 도의 경우 k = 360° 또는 그라디언스의 경우 400 그라디언스).
이렇게 정의된 θ의 값은 원의 크기와 무관합니다. 반지름의 길이가 변경되면 호 길이가 동일한 비율로 변경되므로 비율 s/r은 변경되지 않습니다.
각도 추가 공준
각도 가산 공준은 만약 B가 각도 AOC의 내부에 있다면,
각도 AOC의 측정값은 각도 AOB의 측정값과 각도 BOC의 측정값의 합입니다.
유닛

역사를 통틀어 각도는 다양한 단위로 측정되어 왔습니다.이것들은 각도 단위로 알려져 있으며, 가장 현대적인 단위는 도(°), 라디안(rad), 그라디언(gradian)이지만, 다른 많은 단위들은 역사를 통해 사용되어 왔습니다.[21]각도 측정의 대부분의 단위는 한 바퀴(즉, 중심에 있는 원의 둘레에 의해 조절되는 각도)가 어떤 정수 n에 대해 n 단위와 같도록 정의됩니다.라디안(및 소수점 하위 배수)과 직경 부분은 두 가지 예외입니다.
국제 수량 체계에서 각도는 무차원 수량으로 정의되며, 특히 라디안 단위는 무차원입니다.이 규칙은 치수 분석에서 각도가 처리되는 방식에 영향을 미칩니다.자세한 내용은 라디안 § 차원 분석을 참조하십시오.
다음 표에는 각도를 나타내는 데 사용되는 몇 가지 단위가 나와 있습니다.
| 이름. | 한 바퀴에 수를 보다 | 정도로 | 묘사 |
|---|---|---|---|
| 라디안의 | 2개 | ≈57°17′ | 라디안은 원의 반지름과 길이가 같은 원의 원둘레에 의해 결정됩니다(n = 2 π = 6.283...).원의 반지름과 길이가 같은 원의 호에 의해 가감된 각도입니다.라디안의 기호는 rad입니다.한 방향은 2 π 라디안이고, 한 라디안은 180°/π 또는 약 57.2958도입니다.특히 수학 텍스트에서 하나의 라디안이 1과 동일하다고 가정하는 경우가 많아 단위 rad가 생략됩니다.라디안은 삼각함수가 라디안일 때 나타나는 만족스럽고 "자연적인" 특성으로 인해 단순하고 실용적인 기하학을 넘어 사실상 모든 수학적 작업에 사용됩니다.라디안은 SI에서 각도 측정의 (유래) 단위입니다. |
| 도 | 360 | 1° | 작은 위첨자 원(°)으로 표시되는 도는 1/360 회전이므로 1 회전은 360°입니다.이 오래된 60진법 하위 단위의 한 가지 장점은 단순 기하학에서 흔히 볼 수 있는 많은 각도들이 도의 전체 개수로 측정된다는 것입니다.도의 분수는 일반적인 십진법 표기법(예: 3.5도에서 3.5도)으로 표기할 수 있지만, "분"과 "초" 60진법 하위 단위(discussed 다음)도 사용되고 있으며, 특히 지리 좌표와 천문학 및 탄도학(n = 360)에서 사용되고 있습니다. |
| 호분 | 21,600 | 0°1′ | 호분(또는 MOA, 호분, 또는 단지 분)은 1/60도 = 1/21,600 회전입니다.이는 단일 소수(')로 표시됩니다.예를 들어, 3° 30'은 3 × 60 + 30 = 210분 또는 3 + 30/60 = 3.5도와 같습니다.10진수 분수가 있는 혼합 형식이 사용되기도 합니다. 예를 들어 3° 5.72' = 3 + 5.72/60도입니다.1해리는 역사적으로 지구의 거대한 원을 따라 있는 호분(arc minute)으로 정의되었습니다(n = 21,600). |
| 호초 | 1,296,000 | 0°0′1″ | 초호(또는 초호)는 1분의 60, 1도의 1/3600(n = 1,296,000).그것은 더블 프라임 (″)으로 표시됩니다.예를 들어, 3° 7' 30 ″는 3 + 7/60 + 30/3600도 또는 3.125도와 같습니다. |
| 졸업을 하다 | 400 | 0°54′ | 그레이드, 그라디언, 또는 곤이라고도 불리는 그레이드.이것은 사분면의 십진법 하위 단위입니다.직각은 100 그라데이션 입니다.1킬로미터는 역사적으로 지구의 자오선을 따라 호의 센티등급으로 정의되었으므로, 1킬로미터는 60진법 해리(n = 400)와 십진법 유사합니다.그레이드는 주로 삼각 측량과 대륙 측량에 사용됩니다. |
| 돌다 | 1 | 360° | 회전은 원의 중심에 있는 원의 둘레에 따라 달라지는 각도입니다.회전은 2개의 π 또는 타우 라디안과 같습니다. |
| 시간각 | 24 | 15° | 천문학적인 시간 각도는 1/24 회전입니다.이 시스템은 별들의 상대적 위치와 같이 하루에 한 번씩 순환하는 물체를 측정할 수 있기 때문에 60진법의 소단위를 분의 시간과 초의 시간이라고 합니다.1시간 = 15° = π/12rad = 1/6 quad = 1/24 turn = 16+2/3 grad와 구별되며 15배 더 큽니다. |
| (나침반) 점 | 32 | 11.25° | 내비게이션에 사용되는 점 또는 바람은 1/32 회전입니다. 1점 = 1/8 직각 = 11.25° = 12.5 눈금입니다.각 포인트는 4/4 포인트로 세분화되어 있기 때문에 한 바퀴는 128입니다. |
| 밀리라디안의 | 2000년 | ≈0.057° | 진정한 밀리라디안은 라디안의 1,000분의 1로 정의되는데, 이것은 한 바퀴를 돌리면 정확히 2000 π mrad (또는 약 6283.185 mrad)와 같다는 것을 의미합니다.화기의 거의 모든 스코프 조준경은 이 정의에 따라 보정됩니다.게다가, 포병과 항해에 사용되는 세 가지 다른 관련된 정의는 종종 '밀'이라고 불리는데, 이것은 대략 밀리라디안과 같습니다.이 세 가지 다른 정의에 따르면, 한 턴은 정확히 0.05625도에서 0.06도(3.375분에서 3.6분) 범위에 걸쳐 6000, 6300, 6400밀리미터를 차지합니다.이에 비해 밀리라디안은 약 0.05729578도(3.43775분)입니다.1 "NATO mil"은 턴의 1/6400으로 정의됩니다.밀리라디안과 마찬가지로, 다른 각각의 정의는 밀리라디안의 가감점의 유용한 성질에 근사합니다. 즉, 1 밀리라디안의 값이 1 km 떨어진 곳에서 볼 수 있듯이 1 m 폭에 의해 감산된 각도와 거의 같습니다(2 π/6400 = 0.0009817...).≈ 1/1000). |
| 이진도 | 256 | 1°33'45" | 이진도(binary degree)는 이진 라디안(binary radian) 또는 브래드(brad) 또는 이진 각도 측정(binary angular measurement, BAM)이라고도 합니다.[22]이진도는 (제한된 정밀도이지만) 각도를 단일 바이트로 효율적으로 표현할 수 있도록 컴퓨팅에 사용됩니다.계산에 사용되는 각도의 다른 측정은 n의 다른 값에 대해 한 턴 전체를 두 개의n 등분으로 나누는 것에 기초할 수 있습니다. |
| π 라디안 | 2 | 180° | 다중 π 라디안(MUL π) 유닛은 RPN 과학 계산기 WP 43S에 구현됩니다.참고 항목: IEEE 754 권장 작업 |
| 사분면의 | 4 | 90° | 한 사분면은 1/4회전이며 직각이라고도 합니다.사분면은 유클리드의 원소에 있는 단위입니다.독일어에서 이 기호는 사분면을 나타내는 데 사용됩니다. 1 quad = 90° = π/2 rad = 1/4 turn = 100 grad. |
| 육분의 | 6 | 60° | 6분은 바빌로니아인들이 사용한 단위로,[27][28] 정도, 분호, 초호는 바빌로니아 단위의 60진법 하위 단위입니다.자와 나침반으로 구성하는 것은 간단합니다.정삼각형의 각도 또는 1/6회전입니다. 1 바빌로니아 단위 = 60° = π/3 rad ≈ 1.047197551 rad. |
| 헥사콘테이드 | 60 | 6° | 헥사콘테이드는 에라토스테네스가 사용하는 단위입니다.그것은 6°와 같으므로, 전체 회전은 60개의 육각형으로 나누어졌습니다. |
| 페커스 | 144에서 180까지 | 2° ~ 2+1/2° | 페쿠스는 약 2° 또는 2+1/2°와 같은 바빌로니아 단위였습니다. |
| 지름부분 | ≈376.991 | ≈0.95493° | (이슬람 수학에서 때때로 사용되는) 직경 부분은 1/60 라디안입니다.하나의 "직경 부분"은 약 0.95493°입니다.한 번에 약 376.991개의 지름 부분이 있습니다. |
| 잠 | 224 | ≈1.607° | 옛 아라비아에서는 한 바퀴를 32 아크남으로 세분화하고, 각 아크남을 7 잠으로 세분화하여 한 바퀴를 224 잠으로 만들었습니다. |
부호각
각도의 측정의 정의가 음의 각도의 개념을 지원하지는 않지만, 양과 음의 각도 값이 일부 기준에 대해 반대 방향의 방향 및/또는 회전을 나타낼 수 있도록 허용하는 규약을 부과하는 것이 종종 도움이 됩니다.
2차원 데카르트 좌표계에서 각도는 일반적으로 두 변으로 정의되며, 꼭짓점은 원점에 있습니다.초기 측은 양의 x축에 있는 반면, 다른 측 또는 종단 측은 초기 측의 측정값으로 라디안, 도 또는 회전으로 정의되며, 양의 각도는 양의 y축을 향한 회전을 나타내고 음의 각도는 음의 y축을 향한 회전을 나타냅니다.직각좌표가 x축에서 오른쪽으로, y축에서 위쪽으로 정의되는 표준 위치로 표시될 때 양의 회전은 시계 반대 방향으로, 음의 주기는 시계 방향으로 표시됩니다.
많은 맥락에서 - θ의 각도는 "한 바퀴 전체에서 θ를 뺀" 각도와 효과적으로 동일합니다.예를 들어 -45°로 표시되는 방향은 360° -45° 또는 315°로 정의되는 방향과 효과적으로 동일합니다.최종 위치는 동일하지만 -45°의 물리적 회전(움직임)은 315°의 회전과 같지 않습니다(예를 들어 먼지가 많은 바닥에서 쉬고 있는 빗자루를 들고 있는 사람의 회전은 바닥에 쓸린 영역의 시각적으로 다른 흔적을 남깁니다).
3차원 기하학에서, "시계방향"과 "시계방향"은 절대적인 의미가 없으므로, 양각과 음각의 방향은 일반적으로 각도의 꼭지점을 통과하고 각도의 광선이 놓인 평면에 수직인 법선 벡터에 의해 결정되는 방향으로 정의되어야 합니다.
항법에서 베어링 또는 방위각은 북쪽에 대해 측정됩니다.관례적으로 위에서 볼 때 베어링 각도는 시계 방향으로 양이므로 45°의 베어링은 북동쪽 방향에 해당합니다.네거티브 베어링은 내비게이션에 사용되지 않으므로 북서 방향은 315°의 베어링에 해당합니다.
등각
- 측정값이 같은 각도(즉, 크기가 같은 각도)는 같거나 합동이라고 합니다.각도는 측정값에 의해 정의되며 각도의 변의 길이에 의존하지 않습니다(예: 모든 직각은 측정값이 동일합니다).
- 종단면을 공유하지만 크기가 한 바퀴의 정수배만큼 다른 두 각도를 공종각이라고 합니다.
- 표준 위치의 모든 각도 θ에 대한 기준 각도(관련 각도라고도 함)는 θ의 종단면과 x축 사이의 양의 예각(양 또는 음)입니다.절차적으로, 특정 각도에 대한 기준 각도의 크기는 각도의 크기 모듈로 1/2 회전, 180° 또는 π 라디안을 취하여 결정될 수 있으며, 각도가 예각이면 정지하고, 그렇지 않으면 180°에서 감소된 크기를 뺀 보조 각도를 취하여 결정될 수 있습니다.예를 들어, 30도 각도는 이미 기준 각도이며, 150도 각도도 30도(180° - 150°)의 기준 각도를 갖습니다.210° 및 510°의 각도는 30도의 기준 각도에도 해당합니다(210° mod 180° = 30°, 510° mod 180° = 150°, 보조 각도가 30°임).
관련수량
각도 단위의 경우 각도 덧셈 공준이 고정되는 것이 정의됩니다.각도 추가 공준이 성립하지 않는 각도와 관련된 일부 양은 다음과 같습니다.
- 기울기 또는 기울기는 각도의 접선과 같고, 기울기는 백분율로 표시되는 경우가 많습니다.매우 작은 값(5% 미만)의 경우 선의 기울기는 수평 방향과의 각도에 대한 라디안 단위의 측정값입니다.
- 두 선 사이의 퍼짐은 유리기하학에서 선 사이의 각도 사인의 제곱으로 정의됩니다.각도의 사인과 보조 각도의 사인이 동일하기 때문에 한 선을 다른 선에 매핑하는 모든 회전 각도는 선 사이의 퍼짐에 대해 동일한 값으로 이어집니다.
- 거의 하지 않지만 각도의 사인과 같은 삼각 함수의 직접적인 결과를 보고할 수 있습니다.
곡선 사이의 각도

선과 곡선 사이의 각도(혼합 각도) 또는 두 교차하는 곡선 사이의 각도(곡선 각도)는 교차점에서 접선 사이의 각도로 정의됩니다.특정한 경우에 다양한 이름이 붙여졌습니다.—양피문자(Gr).ἀμ φί, 양면, κυρτός, 볼록) 또는 시소이달(Gr.κισσός, 담쟁이덩굴), 쌍볼록; xystroidal 또는 sistroidal (Gr.긁는 도구인 ξυστρίς), 요철(concavo-convex); 암피코엘릭(Gr.κοίλη, 속이 비어 있음) 또는 각진 달구, 쌍굴(biconcave.
각도를 이등분 및 삼등분하기
고대 그리스 수학자들은 나침반과 직선만을 사용하여 각도를 이등분하는 방법을 알고 있었지만 특정 각도만을 분할할 수 있었습니다.1837년, 피에르 완첼은 이 공사가 대부분의 각도에서 수행될 수 없다는 것을 보여주었습니다.
점 제품 및 일반화
유클리드 공간에서, 두 유클리드 벡터 u와 v 사이의 각도 θ은 공식에 의해 그들의 점곱과 그들의 길이와 관련이 있습니다.
이 공식은 정규 벡터로부터 두 평면(또는 곡면) 사이의 각도와 벡터 방정식으로부터 스큐 선 사이의 각도를 쉽게 구할 수 있는 방법을 제공합니다.
내품
추상적인 실제 내부 제품 공간에서 각도를 정의하기 위해, 우리는 유클리드 점 곱 ( · )을 내부 제품 ⟨ ⋅,⋅ ⟩ 즉 우리는 유클리드 점 곱 ( · )으로 대체합니다.
복잡한 내부 제품 공간에서 위 코사인에 대한 식은 비유의 값을 줄 수 있으므로 로 대체됩니다.
또는 더 일반적으로 절대값을 사용합니다.