Binära talsystemet
Det binära talsystemet är grundat på talbasen 2 och utnyttjar endast två siffror, vanligen 0 och 1. Liksom i det decimala talsystemet är siffran längst till höger minst signifikant. Med en siffra kan endast talen 0 och 1 skrivas. För att skriva talet 2 måste ytterligare en siffra skrivas till vänster om den första, det vill säga '10', varpå talet 3 följer representerat som '11', etcetera.
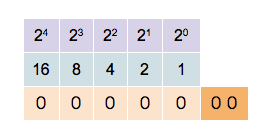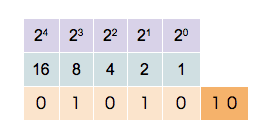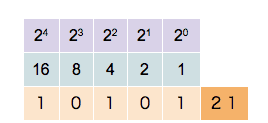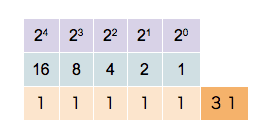
Användning och historik
redigeraBinär talrepresentation används i praktiken i alla datorer eftersom dessa nyttjar digital elektronik. Det binära talsystemet är naturligt och effektivt i de fall där logiskt resonerande överförts till kalkyl. Detta sker inom den booleska algebran, där de logiska sanningsvärdena, falskt och sant representeras av talen 0 respektive 1.
I Europa var Caramuel på 1600-talet först med att beskriva det binära talsystemet som han då kallade dyadik, medan Gottfried Leibniz gjorde det känt för en bredare publik. Talsystemet uppfanns dock långt tidigare av den indiske matematikern Pingala, men blev inte känt i västerlandet förrän omkring år 200 i den gregorianska kalendern.
Talen 0 till 10 i det decimala systemet kan skrivas som de binära talen
Det hexadecimala talsystemet med talbasen 16, har de 16 siffrorna
där varje siffras underliggande representation är en grupp av fyra binära siffror
Av praktiska skäl brukar datatekniker inte använda det binära talsystemet direkt i text, utan det är det hexadecimala talsystemet som används eftersom det är mycket kompaktare. Teknikerna har lärt sig vilken grupp av fyra binära siffror som varje hexadecimalt tal motsvarar.
Egyptierna använde det binära talsystemet för att skriva bråktal i decimalform. De använde sig dock inte av nollor och ettor, utan av en symbol kallad 'Horus öga'. Olika delar av symbolen motsvarade olika positioner på höger sida om kommatecknet. Om just den delen ritades ut motsvarade det en etta på den positionen, om den utelämnades motsvarade det en nolla.[1]
Exempel på konvertering från ett binärt tal till ett decimalt tal:
Om det binära talet är 10101101 så motsvaras det av det decimala talet
Om ett binärkomma förekommer i talet så representeras siffrorna till höger om binärkommat av 2-potenser med negativ exponent:
det vill säga, motsvarande decimala tal är
I datorsammanhang används dock ofta andra representationer av decimaltal, vanligast är flyttalsrepresentation.
I det binära talsystemet sker multiplikation med 2 genom att skifta alla siffror en position åt vänster och placera en nolla som minst signifikanta siffra (i analogi med multiplikation med 10 i det decimala systemet):
Negativa tal brukar hanteras i tvåkomplementsform, en form som gör att addition och subtraktion fungerar utan särskild hantering.
Omvandlare
redigera| Bas | Namn | Tal | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | Binära talsystemet | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | 10000 |
| 3 | Ternära talsystemet | 0 | 1 | 2 | 10 | 11 | 12 | 20 | 21 | 22 | 100 | 101 | 102 | 110 | 111 | 112 | 120 | 121 |
| 4 | Kvarternära talsystemet | 0 | 1 | 2 | 3 | 10 | 11 | 12 | 13 | 20 | 21 | 22 | 23 | 30 | 31 | 32 | 33 | 100 |
| 5 | Kvinära talsystemet | 0 | 1 | 2 | 3 | 4 | 10 | 11 | 12 | 13 | 14 | 20 | 21 | 22 | 23 | 24 | 30 | 31 |
| 6 | Senära talsystemet | 0 | 1 | 2 | 3 | 4 | 5 | 10 | 11 | 12 | 13 | 14 | 15 | 20 | 21 | 22 | 23 | 24 |
| 7 | Septenära talsystemet | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 20 | 21 | 22 |
| 8 | Oktala talsystemet | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 20 |
| 9 | Nonära talsystemet | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 10 | Decimala talsystemet | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 11 | Undecimala talsystemet | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | 10 | 11 | 12 | 13 | 14 | 15 |
| 12 | Duodecimala talsystemet | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | 10 | 11 | 12 | 13 | 14 |
| 13 | Tridecimala talsystemet | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | 10 | 11 | 12 | 13 |
| 14 | Tetradecimala talsystemet | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | 10 | 11 | 12 |
| 15 | Pentadecimala talsystemet | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | 10 | 11 |
| 16 | Hexadecimala talsystemet | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 |
Se även
redigeraReferenser
redigera- P-E Danielsson, Digital Teknik, Studentlitteratur, Lund 1969.
Noter
redigera- ^ ”Eye of Horus Fractions” (PDF). Journal of Health Research College of Public Health Sciences Chulalongkorn University. http://www.cph.chula.ac.th/J%20Health%20Res/files/FullText/23/3/indisecover.pdf. Läst 6 augusti 2010.[död länk]