Hasse-diagram

Een hasse-diagram is in de wiskunde een grafische voorstelling van een eindige verzameling met een partiële orde. Het diagram is genoemd naar de Duitse wiskundige Helmut Hasse (1898–1979). Een hasse-diagram van een partieel geordende verzameling is de graaf met de transitieve reductie van die verzameling, zonder de relatie van elementen met zichzelf aan te geven. In het hasse-diagram worden de elementen van de verzameling getekend als punten en de ordeningsrelatie weergegeven door twee elementen die elkaars directe opvolger en voorganger zijn, te verbinden door een lijn en de grootste van de twee hoger te tekenen dan de kleinste. Dus als ${\displaystyle x\leq y}$ en er is geen element tussen deze twee, zodat ${\displaystyle x}$ een directe voorganger is van ${\displaystyle y}$, wordt ${\displaystyle y}$ hoger dan ${\displaystyle x}$ geplaatst en beide door een lijn verbonden. Op deze manier ontstaat een overzichtelijke voorstelling van de ordening. Zouden we alle vergelijkbare elementen verbinden, dan zou door de veelheid van lijnen vaak een onoverzichtelijke wirwar ontstaan. Voor willekeurige ${\displaystyle x}$ en ${\displaystyle y}$ geldt ${\displaystyle x\leq y}$ als er een route van ${\displaystyle x}$ naar ${\displaystyle y}$ is die steeds naar boven leidt (als ${\displaystyle x=y}$ is dit de triviale "route" via nul lijnen). Als er niet zo'n route is dan heeft het lager, even hoog of hoger liggen van ${\displaystyle x}$ ten opzichte van ${\displaystyle y}$ geen betekenis.

Hasse-diagrammen lenen zich er goed voor een tralie weer te geven. Er volgen in totaal drie voorbeelden van een tralie, waarvan het hasse-diagram in een afbeelding wordt geïllustreerd, voor het derde voorbeeld drie mogelijkheden, met daar tussendoor enig commentaar.

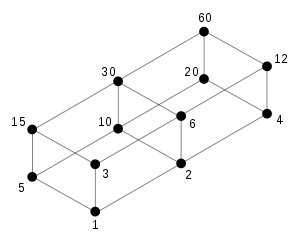
• De verzameling ${\displaystyle V=\{1,2,3,4,5,6,10,12,15,20,30,60\}}$ van alle delers van het getal 60, is partieel geordend door de relatie "deelbaar door".

• De verzameling van alle partities van de verzameling ${\displaystyle \{1,2,3,4\}}$ is partieel geordend door de relatie "verfijning", dat wil zeggen een partitie is 'fijner' als minstens een van de deelverzamelingen uit de partitie verder opgedeeld is.

Op het eerste gezicht lijkt het niet ingewikkeld een hasse-diagram te tekenen. Het blijkt echter tamelijk moeilijk een goed diagram te maken. Er zijn voor een gegeven partieel geordende verzameling namelijk veel verschillende mogelijkheden die in een hasse-diagram weer te geven. Sommige daarvan belichten het ene aspect, zoals interne symmetrieën, andere tonen beter een bepaalde structuur. Het derde voorbeeld laat het probleem duidelijk zien.

• Van de verzameling ${\displaystyle \{a,b,c,d\}}$ is de machtsverzameling, die bestaat uit de 16 deelverzamelingen, een partieel geordende verzameling door de relatie "deelverzameling". Er worden hier drie manieren gegeven om daarvan een hasse-diagram te tekenen.

De deelverzamelingen zijn niet met name genoemd, maar zijn eenvoudig te herkennen. Het linker diagram is waarschijnlijk de meest voor de hand liggende voorstelling. De vijf lagen in het diagram vertegenwoordigen de aantallen elementen in de deelverzamelingen. Het middelste diagram toont de projectie van een hyperkubus en het rechter diagram toont duidelijk de interne symmetrie.

• Hieronder staan de graaf met een verzameling met een strikte partiële orde en daarnaast het hasse-diagram van de bijbehorende partiële orde. De linker graaf is geen graaf van een verzameling met een partiële orde, omdat de reflexieve relaties, dus van de elementen naar zichzelf, er niet in worden aangegeven. Als wordt afgesproken dat de reflexieve relaties niet worden weergegeven, is er geen verschil met de graaf van de strikte partiële orde.

Er zijn verschillende algoritmen bedacht om goede diagrammen te tekenen, maar tot nu toe is menselijke hulp daarbij onontbeerlijk en ook dan is praktische ervaring beslist nodig.

• Relations. met een paragraaf over hasse-diagrammen
• MathWorld. Hasse Diagram.