၂

← 1 2 3 →
-1 0 1 2 3 4 5 6 7 8 9 → List of numbers — Integers ← 0 10 20 30 40 50 60 70 80 90 →
Cardinal	နှစ်
Ordinal	2nd (second / twoth)
Numeral system	binary
Factorization	prime
Gaussian integer factorization	${\displaystyle (1+i)(1-i)}$
Prime	1st
Divisors	1, 2
Greek numeral	Β´
Roman numeral	II, ii
Greek prefix	di-
Latin prefix	duo- bi-
Old English prefix	twi-
Binary	Script error: The function "10to2" does not exist.2
Ternary	Script error: The function "10to3" does not exist.3
Octal	Script error: The function "10to8" does not exist.8
Duodecimal	Script error: The function "10to12" does not exist.12
Hexadecimal	Script error: The function "10to16" does not exist.16
Greek numeral	β'
Arabic, Kurdish, Persian, Sindhi, Urdu	٢
Ge'ez	፪
Bengali	২
Chinese numeral	二，弍，貳
Devanāgarī	२
Telugu	౨
Tamil	௨
Kannada	೨
Hebrew	ב
Khmer	២
Thai	๒
Georgian	Ⴁ/ⴁ/ბ(Bani)

၂ (နှစ်) သည် ကိန်း၊ ဂဏန်း၊ ဂဏန်းခြေ၊ အပေါင်းကိန်း တခု ဖြစ်သည်။ ၁ နှင့် ၃ ကြား နေသော သဘာဝကိန်း ဖြစ်သည်။ တလုံးတည်းသော အငယ်ဆုံး စုံကိန်း သုဒ္ဓကိန်း ဖြစ်သည်။ နှစ်ဖက်သွားဟူသော သဘောသဘာဝကြောင့် ကမ္ဘာ့ယဉ်ကျေးမှု များစွာဝယ် ဘာသာရေးနှင့် ဝိညာဉ်ပိုင်းဆိုင်ရာတွင် အရေးပါသည်။

၂ (အသံထွက်-နှစ်)သည် မြန်မာဘာသာတွင် သင်္ချာဘာသာသင်ကြားရာတွင် အသုံးပြုပြီး တစ်ထက်တစ်ဆပိုသော နှစ်အတွက်အသုံးပြုသော သင်္ချာဂဏန်းအက္ခရာတစ်ခုဖြစ်သည်။ နှစ်ကို ဒုတိယဟုလဲ ခေါ်သည်။ အင်္ဂလိပ်ဘာသာတွင် 2 ဟုရေးသားကြသည်။

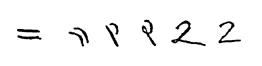
မျက်မှောက် အနောက်တိုင်းကမ္ဘာတွင် အသုံးပြုသော ဂဏန်းခြေ ၂ ၏ မူလရင်းမြစ် ဖြစ်သော အိန္ဒိယ ဗြဟ္မီ စာသားများသို့ ခြေရာပြန်ကောက်လိုက်သော်၊ ၂ ကို အလျားလိုက် မျဉ်းနှစ်ကြောင်းအဖြစ် ရေးသားထားသည်။ မျက်မှောက် တရုတ်နှင့် ဂျပန်စာရေးသားနည်းတွင် ဤနည်းကို သုံးဆဲ ဖြစ်သည်။ ဂုပ္တ အရေးအသားတွင် မျဉ်းနှစ်ကြောင်းကို ၄၅ ဒီဂရီ စောင်းလိုက်ရာ၊ အစောင်းများ ဖြစ်သွားသည်။ ထိပ်မျဉ်းသည် တခါတရံ တိုတတ်ကာ၊ ၎င်း၏ အောက်စွန်းသည် အောက်ခြေမျဉ်း၏ အလယ်သို့ ကွေးညွတ်သွားသည်။ ဒေဝနဂရီ အရေးအသားတွင် ထိပ်မျဉ်းကို အောက်မျဉ်းနှင့် ထိသွားအောင် ကောက်၍ ရေးသည်။ အာရဗီ ဂူဘာအရေးအသားတွင် အောက်မျဉ်းမှာ လုံးဝ တည့်မတ်နေကာ၊ ဂဏန်းသည် အစက်မပါသော မေးခွန်းမှတ်နှင့် ဆင်တူသည်။ ထိုတည့်နေသော အောက်မျဉ်းကို မူလအတိုင်း အလျားလိုက် ပြန်ထား၍ အပေါ်မျဉ်းကွေးကို အကွေးအတိုင်း ထားလိုက်ပုံက ယနေ့ အသုံးပြုနေသော 2 ပုံစံ ဖြစ်လာသည်။^[၁]

အချို့ဖောင့်များတွင်၊ ဂဏန်းခြေ ၂ သည် x-အမြင့်သာ ရှိသည်။ ဥပမာ -

နှစ် သည် အင်္ဂလိပ်ဟောင်း twá(ဣတ္ထိလိင်), tú(နပုလ္လိင်), twégen(ပုလ္လိင်) မှ ဆင်းသက်လာပြီး၊ ယနေ့အခါ twegen မှနေ၍ twain ဟု ကျန်ရစ်သည်။^[၂]

၂ ဖြင့် စား၍ ပြတ်လျှင် ထိုကိန်းသည် စုံကိန်း ဖြစ်သည်။ ကိန်းဂဏန်းအားဖြင့် ကိန်းပြည့်ဖြစ်စေ၊ ဒသမဖြင့် ရေးသည် ဖြစ်စေ၊ ၂ ဖြင့် စား၍ ပြတ်မပြတ်ကို သိလိုမူ ထိုကိန်း၏ နောက်ဆုံးလုံးကိုသာ ကြည့်ရန် လိုသည်။ နောက်ဆုံးကိန်းကို နှစ်ဖြင့် စားပြတ်လျှင် ကိန်းတခုလုံးသည် ၂ ဖြင့် စားပြတ်သည်။ နောက်ဆုံးကိန်းသည် စုံကိန်းဖြစ်လျှင် ကိန်းတခုလုံးသည် စုံကိန်း ဖြစ်သည် ဟူလို။ အထူးအားဖြင့်၊ ၂ အလီအတိုင်း ၀၊ ၂၊ ၄၊ ၆ နှင့် ၈ တို့ဖြင့် ဆုံးသတ်ပေမည်။

နှစ်သည် အငယ်ဆုံး သုဒ္ဓကိန်း ဖြစ်ကာ၊ တခုတည်းသော စုံ သုဒ္ဓကိန်း ဖြစ်သည့်အတွက် ရံခါ အဆန်းဆုံး သုဒ္ဓကိန်း ခေါ်သည်။^[၃] နောက် သုဒ္ဓကိန်းမှာ သုံး ဖြစ်သည်။ နှစ်နှင့် သုံးသည် တခုတည်းသော ဆက်တိုက်လာသည့် သုဒ္ဓကိန်း နှစ်လုံး ဖြစ်သည်။ ၂ သည် ပထမဆုံး ဆိုဖီ ဂျာမိန်း သုဒ္ဓကိန်း၊ ပထမဆုံး ဆခွဲနိုင်သော သုဒ္ဓကိန်း၊ ပထမဆုံး လူကပ်စ် သုဒ္ဓကိန်းနှင့် ပထမဆုံး ရာမနူဂျန် သုဒ္ဓကိန်း ဖြစ်သည်။^[၄]

နှစ်သည် တတိယ သို့မဟုတ် စတုတ္ထ ဖီဘိုနာစီ ကိန်း ဖြစ်သည်။

နှစ်သည် ဘိုင်နရီစနစ်၏ အခြေ ဖြစ်သည်။ ဤ ဘိုင်နရီ နံပါတ်စနစ်ကို ကွန်ပျူတာတွင် ချဲ့ထွင် သုံးပြုသည်။ (log₂ n tokens)

မည်သည့် ကိန်း အတွက်မဆို x:

x + x = 2 · x အပေါင်းမှ အမြှောက်သို့

x · x = x² အမြှောက်မှ ထပ်ကိန်းသို့

x^x = x↑↑2 ထပ်ကိန်းမှ tetration သို့

Hyperoperation အမှတ်အသားကို မိတ်ဆက်ခြင်းဖြင့် ဤ ကိန်းစဉ်၏ လုပ်ဆောင်ချက်ကို ဤနေရာတွင် "hyper(a,b,c)" ဟု သတ်မှတ်ပြီး၊ a နှင့် c သည် ပထမနှင့် ဒုတိယ operand ဖြစ်ကာ၊ b မှာ အထက်လုပ်ဆောင်ချက် ပုံကြမ်းကိန်းစဉ်တွင် level ဖြစ်သည်။ ယေဘုယျအားဖြင့် အောက်ပါအတိုင်း ဖြစ်သည်။

hyper(x,n,x) = hyper(x,(n + 1),2)

သို့ဖြစ်၍ နှစ်တွင် အတုမရှိသော ဂုဏ်သတ္တိ ရှိသည်။ 2 + 2 = 2 · 2 = 2² = 2↑↑2 = 2↑↑↑2 = ... တွင် Knuth ၏ မြားထောင်မှတ်ဖြင့် မှတ်သားသည်။ ထောင်မြား အရေအတွက်သည် hyperoperation ၏ လယ်ဗယ်ကို ညွှန်းသည်။

နှစ်သည် ပြန်တူနေသော သဘာဝ x ထပ်ကိန်း၏ အပြန်အလှန် ပေါင်းလဒ်ကဲ့သို့သော တခုတည်းသော x ကိန်း ဖြစ်သည်။ သင်္ကေတအားဖြင့်

${\displaystyle \sum _{k=0}^{\infty }{\frac {1}{2^{k}}}=1+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+\cdots =2.}$

ယင်းမှာ

${\displaystyle \sum _{k=0}^{\infty }{\frac {1}{n^{k}}}=1+{\frac {1}{n-1}}\quad {\mbox{for all}}\quad n\in \mathbb {R} >1.}$

ဟူသော အချက်မှ လာသည်။

နှစ်၏ ထပ်ကိန်းများသည် မာဆင်နီ သုဒ္ဓကိန်းများ အယူအဆ၏ အချက်အချာ ဖြစ်ကာ၊ ကွန်ပျူတာသိပ္ပံအတွက် အရေးပါသည်။ နှစ်သည် ပထမဆုံး မာဆင်နီသုဒ္ဓထပ်ညွှန်း ဖြစ်သည်။

ဂဏန်းတခုကို နှစ်ထပ်ကိန်းရင်း ယူပုံသည် သာမန် သင်္ချာ တွက်ချက်မှု ဖြစ်ကာ၊ နှစ်ထပ်ကိန်းရင်း သင်္ကေတပေါ်ရှိ နေရာတွင် ထပ်ညွှန်းကို သာမန်အားဖြင့် သုံးထပ် သို့ အခြား ထပ်များ ရေးသားလေ့ ရှိပြီး၊ ဘာမှ ရေးမထားလျှင် နှစ်ထပ်ကိန်းရင်းကို ရှာခိုင်းခြင်း ဖြစ်သည်ဟု အလိုလို နားလည်ရပေသည်။

၂ ၏ နှစ်ထပ်ကိန်းရင်းသည် ပထမဆုံး သိမြင်ရသည့် ရာရှင်နယ်မဟုတ်သော ကိန်း ဖြစ်သည်။

အငယ်ဆုံး field တွင် အစုဝင် element ၂ ခု ရှိသည်။

သဘာဝကိန်းများ ၏ set-theory တည်ဆောက်ပုံတခုတွင်၊ ၂ ကို {{∅},∅} အစုနှင့် ခွဲခြားသည်။ နောက်အစုသည် ကဏ္ဍသီအိုရီတွင် အရေးပါသည်။ ၎င်းသည် အစုများ၏ ကဏ္ဍတွင် subobject classifier တခု ဖြစ်သည်။

နှစ်တွင် အောက်ပါ ထူးခြားချက်လည်း ရှိသည်။

${\displaystyle \sum _{k=0}^{n-1}2^{k}=2^{n}-1}$

a သည် သုညနှင့် မညီခြင်းအတွက်

${\displaystyle \sum _{k=a}^{n-1}2^{k}=2^{n}-\sum _{k=0}^{a-1}2^{k}-1}$

မည်သည့် n ဒိုင်မင်ရှင်းတွင် မဆို ထင်ရှားသည့် အမှတ်နှစ်ခုသည် မျဉ်းဖြောင့် ဖြစ်ခြင်းကို ဆုံးဖြတ်ပေးသည်။

စက်လုံးတခုသို့ မည်သည့် မျက်နှာပြင်မဆို ပုံဖော်မှုအတွက်၊ ယူလာ ဂုဏ်သတ္တိ Euler characteristic မှာ χ = V − E + F = 2 ဖြစ်၍၊ V မှာ ဆုံစက်များ အရေအတွက်၊ E မှာ အနားများ အရေအတွက်နှင့် F မှာ မျက်နှာပြင်များ အရေအတွက် ဖြစ်သည်။ (Vertices, edges, and faces)