Viskoelastisuus

Viskoelastisuus on materiaalin ominaisuus, jossa yhdistyvät sekä viskositeettiset että elastiset ominaisuudet muodonmuutoksen aikana.^[1]

Lineaarinen viskoelastisuus:

${\displaystyle \epsilon (t)={\frac {\sigma (t)}{E_{\text{inst,creep}}}}+\int _{0}^{t}K(t-t^{\prime }){\dot {\sigma }}(t^{\prime })dt^{\prime }}$

tai

${\displaystyle \sigma (t)=E_{\text{inst,relax}}\epsilon (t)+\int _{0}^{t}F(t-t^{\prime }){\dot {\epsilon }}(t^{\prime })dt^{\prime }}$

missä

• t on aika
• ${\displaystyle \sigma (t)}$ on jännitys
• ${\displaystyle \epsilon (t)}$ on venymä
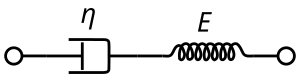
• ${\displaystyle E_{\text{inst,creep}}}$ ja ${\displaystyle E_{\text{inst,relax}}}$ ovat hetkelliset elastisuuskertoimet
• K(t) on viruminen
• F(t) on relaksaatio

Maxwellin malli voi edustaa viskoosivaimenninta ja elastista jousta kytkettyna sarjaan, kuten kuvassa näkyy. Malli voidaan esittää seuraavan yhtälön avulla:

${\displaystyle {\frac {d\epsilon }{dt}}={\frac {d\epsilon _{D}}{dt}}+{\frac {d\epsilon _{S}}{dt}}={\frac {\sigma }{\eta }}+{\frac {1}{E}}{\frac {d\sigma }{dt}}}$.