Octagrama
| Octagrama | ||
|---|---|---|
 Octagrama regular | ||
| Características | ||
| Tipo | Polígono estrellado | |
| Lados | 8 | |
| Vértices | 8 | |
| Grupo de simetría | D8 | |
| Símbolo de Schläfli |
{8⁄3} t{4⁄3} | |
| Diagrama de Coxeter-Dynkin |
| |
| Polígono dual | Autodual | |
| Ángulo interior | 45° | |
| Propiedades | ||
| Estrellado, Cíclico, Isogonal, Isotoxal y Equilátero | ||
En geometría, un octagrama es un polígono estrellado de ocho ángulos. El nombre octagrama combina un prefijo de número griego, octa-, con el sufijo griego -gram . El sufijo -gram deriva de γραμμή (grammḗ) que significa "recta".[1]
Detalle
[editar]En general, un octagrama es cualquier octágono auto intersectante (polígono de 8 lados).
Al octagrama regular le corresponde el símbolo de Schläfli {8/3}, que significa una estrella de 8 lados, conectando cada vértice (con la misma distribución que los de un octógono regular) con otro vértice situado tres lugares más adelante.
Variaciones
[editar]Estas variaciones tienen una simetría diedral inferior, Dih4:
 Estrecho  Ancho (45 grados de rotación) |
  Isotoxal |
 Bandera de Chile histórica, incluyendo una estrella octogonal con sus trazos internos eliminados (el Guñelve) |
 La geometría se puede ajustar para que 3 bordes se crucen en un solo punto, como el símbolo de Auseklis |
 Una rosa de los vientos de 8 puntos puede verse como una estrella octogonal, con 4 puntos primarios y 4 puntos secundarios |
El símbolo de la Estrella Tartésica está representada en el glifo Unicode ۞, con el código U+06DE.
Como un cuadrado cuasitruncado
[editar]Los truncamientos más profundos del cuadrado pueden producir formas de polígonos estrellados intermedias isogonales (vértice-transitivos) con vértices igualmente espaciados y lados de dos longitudes. Un cuadrado truncado es un octógono, t {4} = {8}. Un cuadrado cuasitruncado, invertido como {4/3}, es un octagrama, t{4/3}={8/3}.[2]
El poliedro estrellado uniforme denominado hexaedro truncado estrellado, t'{4,3}=t{4 /3,3} tiene caras con forma de octagrama construidas a partir del cubo de esta manera.
| Regular | Quasirregular | Isogonal | Quasirregular |
|---|---|---|---|
 {4} |
 t{4}={8} |

|
 t'{4}=t{4/3}={8/3} |
| Regular | Uniforme | Isogonal | Uniforme |
 {4,3} |
 t{4,3} |

|
 t'{4,3}=t{4/3,3} |
Compuestos de polígonos estrellados
[editar]Hay dos figuras estrelladas octagrámicas regulares (compuestas) de la forma {8 /k}. La primera está construida como dos cuadrados {8/2}=2{4}, y la segunda como cuatro digonos degenerados, {8/4}=4{2}. Hay otros compuestos isogonales e isotoxales que incluyen formas rectangulares y rómbicas.
| Regular | Isogonal | Isotoxal | ||
|---|---|---|---|---|
 a{8}={8/2}=2{4} |
 {8/4}=4{2} |

|

|

|
El octagrama {8/2} o 2{4}, como diagrama de Coxeter ( +
), se pueden ver como el equivalente 2D del compuesto de cubo y octaedro 3D (
+
), del compuesto de teseracto y 16 células 4D (
+
), y del compuesto de 5 cubos y 5-ortoplex 5D; es decir, el compuesto de un n-cubo y de un politopo de cruce en sus respectivas posiciones duales.
Otras representaciones de una estrella octogonal
[editar]Una estrella octogonal puede tener el aspecto de un hexadecágono cóncavo, con la geometría de intersección interna eliminada. También se puede diseccionar por líneas radiales.
| 2 {4} | 
|

|

|

|
|---|---|---|---|---|
| {8/3} | 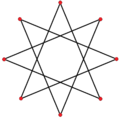
|
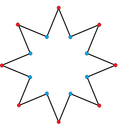
|

|

|
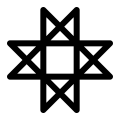
|

|

|

| |

|

|
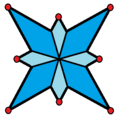
|

|
Otros usos
[editar]- En Unicode, el símbolo "Asterisco de ocho radios" ✳ es U + 2733.
Véase también
[editar]- Uso
- Estrella de ocho puntas
- Rub el Hizb: carácter islámico
- Estrella de Ishtar: símbolo de la antigua diosa semita oriental Ishtar y su contraparte sumeria Inanna
- Estrella de Lakshmi: personaje indio Laksmí
- Surya Majapahit: uso durante los tiempos de Majapahit en Indonesia, para representar a los dioses hindúes de las direcciones
- Rosa de los vientos con los puntos del compás: uso en las brújulas para representar los puntos cardinales de los ocho vientos principales
- Guñelve: representación del planeta Venus en la iconografía mapuche
- Auseklis: octagrama regular utilizado por los letones
- Selburose: nombre del octagrama regular de origen noruego
- Estrellas en general
Referencias
[editar]- ↑ γραμμή, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- ↑ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum
Bibliografía
[editar]- Grünbaum, B. and G.C. Shephard; Tilings and Patterns, New York: W. H. Freeman & Co., (1987), ISBN 0-7167-1193-1.
- Grünbaum, B.; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993), ed T. Bisztriczky et al., Kluwer Academic (1994) pp. 43–70.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 404: Regular star-polytopes Dimension 2)
Enlaces externos
[editar]Wikimedia Commons alberga una categoría multimedia sobre Octagrama.
- Weisstein, Eric W. «Octagram». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
