Planar lamina

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Planar lamina" – news · newspapers · books · scholar · JSTOR (October 2021) (Learn how and when to remove this message) This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (October 2015) (Learn how and when to remove this message) (Learn how and when to remove this message)

In mathematics, a planar lamina (or plane lamina^[1]) is a figure representing a thin, usually uniform, flat layer of the solid. It serves also as an idealized model of a planar cross section of a solid body in integration.

Planar laminas can be used to determine moments of inertia, or center of mass of flat figures, as well as an aid in corresponding calculations for 3D bodies.

A planar lamina is defined as a figure (a closed set) D of a finite area in a plane, with some mass m.^[2]

This is useful in calculating moments of inertia or center of mass for a constant density, because the mass of a lamina is proportional to its area. In a case of a variable density, given by some (non-negative) surface density function ${\displaystyle \rho (x,y),}$ the mass ${\displaystyle m}$ of the planar lamina D is a planar integral of ρ over the figure:^[3]

${\displaystyle m=\iint _{D}\rho (x,y)\,dx\,dy}$

The center of mass of the lamina is at the point

${\displaystyle \left({\frac {M_{y}}{m}},{\frac {M_{x}}{m}}\right)}$

where ${\displaystyle M_{y}}$ is the moment of the entire lamina about the y-axis and ${\displaystyle M_{x}}$ is the moment of the entire lamina about the x-axis:

${\displaystyle M_{y}=\lim _{m,n\to \infty }\,\sum _{i=1}^{m}\,\sum _{j=1}^{n}\,x{_{ij}}^{*}\,\rho \ (x{_{ij}}^{*},y{_{ij}}^{*})\,\Delta D=\iint _{D}x\,\rho \ (x,y)\,dx\,dy}$

${\displaystyle M_{x}=\lim _{m,n\to \infty }\,\sum _{i=1}^{m}\,\sum _{j=1}^{n}\,y{_{ij}}^{*}\,\rho \ (x{_{ij}}^{*},y{_{ij}}^{*})\,\Delta D=\iint _{D}y\,\rho \ (x,y)\,dx\,dy}$

with summation and integration taken over a planar domain ${\displaystyle D}$.

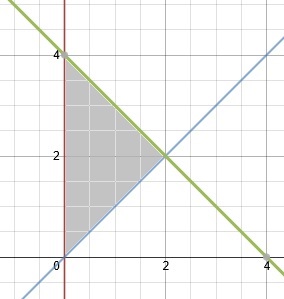
Find the center of mass of a lamina with edges given by the lines ${\displaystyle x=0,}$ ${\displaystyle y=x}$ and ${\displaystyle y=4-x}$ where the density is given as ${\displaystyle \rho \ (x,y)\,=2x+3y+2}$.

For this the mass ${\displaystyle m}$ must be found as well as the moments ${\displaystyle M_{y}}$ and ${\displaystyle M_{x}}$.

Mass is ${\displaystyle m=\iint _{D}\rho (x,y)\,dx\,dy}$ which can be equivalently expressed as an iterated integral:

${\displaystyle m=\int _{x=0}^{2}\int _{y=x}^{4-x}\,(2x+3y+2)\,dy\,dx}$

The inner integral is:

${\displaystyle \int _{y=x}^{4-x}\,(2x+3y+2)\,dy}$

${\displaystyle \qquad =\left.\left(2xy+{\frac {3y^{2}}{2}}+2y\right)\right|_{y=x}^{4-x}}$

${\displaystyle \qquad =\left[2x(4-x)+{\frac {3(4-x)^{2}}{2}}+2(4-x)\right]-\left[2x(x)+{\frac {3(x)^{2}}{2}}+2(x)\right]}$

${\displaystyle \qquad =-4x^{2}-8x+32}$

Plugging this into the outer integral results in:

${\displaystyle {\begin{aligned}m&=\int _{x=0}^{2}\left(-4x^{2}-8x+32\right)\,dx\\&=\left.\left(-{\frac {4x^{3}}{3}}-4x^{2}+32x\right)\right|_{x=0}^{2}\\&={\frac {112}{3}}\end{aligned}}}$

Similarly are calculated both moments:

${\displaystyle M_{y}=\iint _{D}x\,\rho (x,y)\,dx\,dy=\int _{x=0}^{2}\int _{y=x}^{4-x}x\,(2x+3y+2)\,dy\,dx}$

with the inner integral:

${\displaystyle \int _{y=x}^{4-x}x\,(2x+3y+2)\,dy}$

${\displaystyle \qquad =\left.\left(2x^{2}y+{\frac {3xy^{2}}{2}}+2xy\right)\right|_{y=x}^{4-x}}$

${\displaystyle \qquad =-4x^{3}-8x^{2}+32x}$

which makes:

${\displaystyle {\begin{aligned}M_{y}&=\int _{x=0}^{2}(-4x^{3}-8x^{2}+32x)\,dx\\&=\left.\left(-x^{4}-{\frac {8x^{3}}{3}}+16x^{2}\right)\right|_{x=0}^{2}\\&={\frac {80}{3}}\end{aligned}}}$

and

${\displaystyle {\begin{aligned}M_{x}&=\iint _{D}y\,\rho (x,y)\,dx\,dy=\int _{x=0}^{2}\int _{y=x}^{4-x}y\,(2x+3y+2)\,dy\,dx\\&=\int _{0}^{2}(xy^{2}+y^{3}+y^{2}){\Big |}_{y=x}^{4-x}\,dx\\&=\int _{0}^{2}(-2x^{3}+4x^{2}-40x+80)\,dx\\&=\left.\left(-{\frac {x^{4}}{2}}+{\frac {4x^{3}}{3}}-20x^{2}+80x\right)\right|_{x=0}^{2}\\&={\frac {248}{3}}\end{aligned}}}$

Finally, the center of mass is

${\displaystyle \left({\frac {M_{y}}{m}},{\frac {M_{x}}{m}}\right)=\left({\frac {\frac {80}{3}}{\frac {112}{3}}},{\frac {\frac {248}{3}}{\frac {112}{3}}}\right)=\left({\frac {5}{7}},{\frac {31}{14}}\right)}$