Moviment circular
A cinemàtica, un moviment circular és un model de moviment en el pla, on el cos que es mou té una trajectòria circular al voltant d'un centre o eix de gir.[1]
La seva formulació i modelització es realitza en coordenades polars, ja que d'aquesta manera resulta més senzilla. Les equacions de moviment descriuen el moviment el centre de massa d'un cos.
Entre els exemples de moviment circular es troba: un satèl·lit artificial orbitant la Terra a una alçada constant, les fulles del ventilador del sostre girant al voltant del centre, una pedra que està lligada a una corda i s'està balancejant en cercles, un cotxe que gira per una corba en una pista de carreres, un electró que es mou perpendicularment a un camp magnètic uniforme i un engranatge girant dins d'un mecanisme.
Conceptes
[modifica]En el moviment circular cal tenir en compte alguns conceptes bàsics de la cinemàtica i dinàmica del mateix:
- Eix de gir: és la línia recta al voltant de la qual es realitza la rotació, aquest eix pot romandre fix o variar amb el temps, però per a cada instant concret és l'eix de la rotació (considerant en aquest cas una variació infinitesimal o diferencial de temps). L'eix de gir defineix un punt anomenat centre de gir de la trajectòria descrita (O).[2]
- Arc: partint d'un centre fix o eix de gir fix, és l'espai recorregut en la trajectòria circular o arc de radi unitari amb el qual es mesura el desplaçament angular. La seva unitat és el radiant (espai recorregut dividit entre el radi de la trajectòria seguida, divisió de longitud entre longitud, adimensional).
- Velocitat angular: és la variació del desplaçament angular per unitat de temps ().
- Acceleració angular: és la variació de la velocitat angular per unitat de temps ().
En dinàmica dels moviments curvilinis, circulars i / o giratoris es tenen en compte a més les següents magnituds:
- Moment angular (L): és la magnitud que en el moviment rectilini equival al moment lineal o quantitat de moviment però aplicada al moviment curvilini, circular i / o giratori (producte vectorial de la quantitat de moviment pel vector posició, des del centre de gir al punt on es troba la massa puntual).
- Moment d'inèrcia (I): és una qualitat dels cossos que depèn de la seva forma i de la distribució de la seva massa i que resulta de multiplicar una porció concreta de la massa per la distància que la separa l'eix de gir.
- Moment de força (M): o parell motor és la força aplicada per la distància a l'eix de gir (és l'equivalent a la força agent del moviment que canvia l'estat d'un moviment rectilini).
Caracterització del moviment circular
[modifica]Posició angular o fase
[modifica]Es representa per les lletres gregues φ o θ indistintament. Indica en quin punt de la trajectòria es troba la partícula. La distància recorreguda al llarg de l'arc es pot trobar amb la següent expressió:
- on:
- és el radi de curvatura
- és la distància lineal recorreguda
- és l'angle girat
Velocitat angular
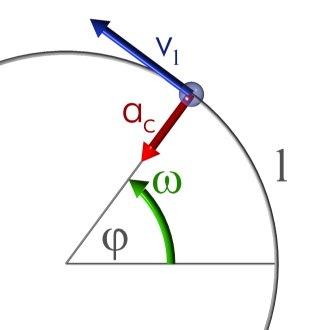
[modifica]Es representa per la lletra grega . És un vector perpendicular al pla on se situa el moviment. El seu mòdul ens indica amb quina rapidesa s'efectua el moviment; i el seu sentit, el sentit de la rotació. Per facilitar els càlculs normalment es treballa com a escalar, utilitzant el signe per diferenciar el sentit de rotació, i es representa amb una fletxa giratòria (vegeu la figura). Matemàticament es defineix el seu mòdul com la derivada de la fase respecte del temps.
La següent expressió ens defineix el vector velocitat lineal en un MC com el producte vectorial de la velocitat angular (perpendicular al pla) i el vector posició de la partícula (que coincideix amb el radi de gir); d'aquesta manera la velocitat és sempre tangent a la trajectòria i perpendicular al radi:
- Vectorialment:
- En mòdul:
Si el seu valor és 0 no hi ha moviment.
Si el seu valor és constant i diferent de 0, tindrem un moviment circular uniforme (MCU).
Si el seu valor depèn linealment del temps, tindrem un moviment circular uniformement accelerat (MCUA).
Prenem l'equació de la posició angular, per a una partícula situada a un radi constant de l'eix de rotació:
on x(t) representa la distància recorreguda sobre l'arc de radi R per on es mou la partícula.
Derivant l'equació anterior respecte del temps s'anul·la un dels termes ja que el radi és constant:
Finalment, aplicant les definicions de velocitat com a derivada de la posició obtenim:
Recordem que la velocitat és un vector paral·lel al pla de gir, perpendicular al radi de gir i tangent al cercle que forma el moviment de la massa. Per tant, podem expressar aquesta mateixa equació vectorialment com a producte vectorial (compleix que el mòdul del producte és producte de móduls i ens proporciona les direccions i sentits correctes als vectors, segons està definit en un sistema de referència a dretes):
Acceleració angular
[modifica]Es representa per la lletra grega . Ens indica la variació de la velocitat angular en el temps. Matemàticament és un vector perpendicular al pla de gir, que s'obté com la derivada del vector velocitat angular () respecte del temps. Substituint l'equació de la fase és possible definir l'acceleració angular en funció d'aquesta. Això és especialment interessant quan tenim la velocitat angular definida en funció de la fase i no del temps.
Si el seu valor és 0, tindrem un moviment circular uniforme (MCU).
Si el seu valor és constant i diferent de 0, tindrem un moviment circular uniformement accelerat (MCUA).
Freqüència
[modifica]La freqüència () es defineix com la quantitat de voltes que es fan en un temps determinat. És, per tant, la inversa del període.
Període
[modifica]El període d'oscil·lació () es defineix com el temps que triga el cos a fer una volta sencera. És, per tant, la inversa de la freqüència.
Dinàmica del moviment circular
[modifica]Acceleració tangencial i acceleració normal
[modifica]En els moviments circulars l'acceleració es pot descompondre en dues components: una de perpendicular a la direcció del moviment, l'acceleració normal o centrípeta, i l'altra en la mateixa direcció que el moviment, l'acceleració tangencial.
L'acceleració tangencial () mesura el canvi de la velocitat del mòbil en el temps. És un vector tangent a la trajectòria i, per tant, paral·lel al vector velocitat lineal. El seu valor pot ser zero (MCU). Matemàticament es defineix com el producte vectorial de l'acceleració angular () per la posició de la partícula ():
- Vectorialment:
- En mòdul:
L'acceleració normal () és aquella provocada per les forces centrípetes que originen el moviment circular. La seva direcció és perpendicular a la trajectòria, apuntant sempre cap al centre de gir. És present en qualsevol moviment circular i el seu mòdul es pot calcular segons la següent expressió:
Substituint la velocitat lineal per la velocitat angular (on ), obtenim:
Aquestes magnituds estan relacionades amb l'acceleració total que suporta la partícula en moviment segons la següent expressió:
- Vectorialment:
- En mòdul:
Donada l'expressió de la velocitat (on considerem el vector posició de la partícula, de mòdul igual al radi), derivem respecte del temps per obtenir la fórmula de l'acceleració total de la partícula:
A partir d'aquí es defineix:
I, per tant:
L'acceleració normal es pot simplificar aplicant :
Força centrípeta
[modifica]És aquella força resultant que crea l'acceleració normal. S'obté com la suma de totes les forces de direcció perpendicular a la trajectòria, considerant positives aquelles que apunten cap al centre de gir i negatives les altres. És per tant perpendicular a la trajectòria de la partícula. La seva existència és imprescindible per obtenir un moviment circular. En mòdul es pot expressar:
Moviment circular uniforme (MCU)
[modifica]Moviment circular amb velocitat angular i mòdul de la velocitat lineal constants. Les acceleracions angular i tangencial seran, per tant, 0.
Per similitud amb el moviment rectilini, donat un angle inicial i una velocitat angular es pot expressar:
Moviment circular uniformement accelerat (MCUA)
[modifica]Moviment circular amb velocitat angular i mòdul de la velocitat linealment dependents del temps. Les acceleracions angular i tangencial seran, per tant, constants i diferents de 0.
Per similitud amb el moviment rectilini, donat un angle inicial , una velocitat angular inicial i una acceleració angular es pot expressar:
Referències
[modifica]- ↑ Knudsen, Jens Martin; Hjorth, Poul Georg. Elements of newtonian mechanics. Berlin: Springer, 2000. ISBN 978-3-540-67652-2.
- ↑ Gómez, R W; Hernández-Gómez, J J; Marquina, V «A jumping cylinder on an inclined plane». European Journal of Physics, 33, 5, 01-09-2012, pàg. 1359–1365. DOI: 10.1088/0143-0807/33/5/1359. ISSN: 0143-0807.