궤도(동역학)

이 글에는 참고문헌, 관련 독서 또는 외부 링크 목록이 수록되어 있으나 인라인 인용구가 부족하여 출처가 불분명하다. 좀 더 정확한 인용문을 도입하여 이 기사를 개선할 수 있도록 도와주십시오. (2013년 2월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

수학에서, 특히 역동적인 시스템에 대한 연구에서, 궤도는 역동적인 시스템의 진화 기능에 관련된 점들의 집합이다. 그것은 시스템이 진화함에 따라 특정한 초기 조건에서 동적 시스템의 궤적으로 덮인 위상 공간의 부분집합으로 이해할 수 있다. 위상 공간 궤적은 주어진 위상 공간 좌표 집합에 대해 고유하게 결정되므로 상공간에서 서로 다른 궤도가 교차하는 것은 불가능하므로 동적 시스템의 모든 궤도의 집합은 위상 공간의 분할이다. 위상학적 방법을 사용하여 궤도의 성질을 이해하는 것은 현대 역동적 시스템 이론의 목표 중 하나이다.

이산 시간 동력학 시스템의 경우 궤도는 시퀀스, 실제 동력학 시스템의 경우 궤도는 곡선, 홀로모픽 동력학 시스템의 경우 궤도는 리만 표면이다.

정의

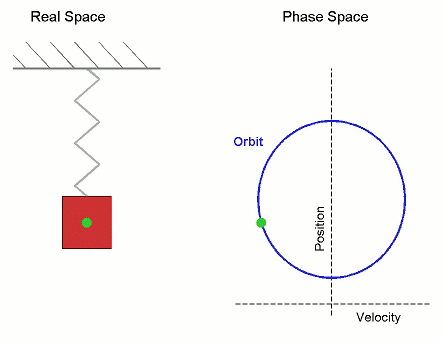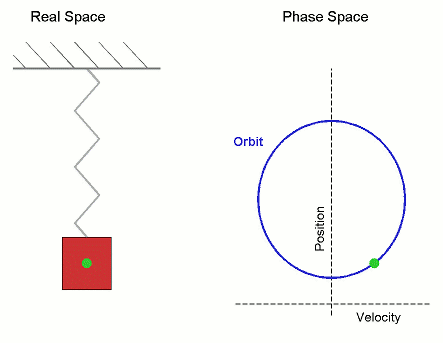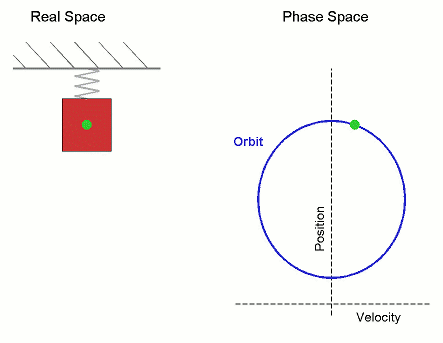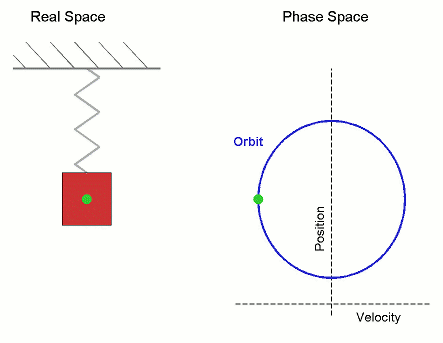
그룹 T로 동적 시스템(T, M, φ)을 부여하고, 집합 M과 φ 진화 함수를 부여한다.

${\displaystyle \Phi$$$$U\to M}$ ${\displaystyle \mathrm{여기}}$서 $U{\displaystyle }$ ${\displaystyle \subset }$ ${\displaystyle T}$ ${\displaystyle \times }$ M ${\displaystyle U\subset T\times M},$${\displaystyle \phi }$ $0$ , $x$)${\displaystyle }$= x ${\displaystyle \Phi$(0,$x)=x}$

우리는 정의한다.

$[\displaystyle I(x):=\{t\in T:(t,x)\in U\}}$

그때의 세트

${\displaystyle \filename _{x=\\{\Phi(t,x):t\in I(x)\}\subset M}$

x를 통한 궤도라고 불린다. 하나의 점으로 구성된 궤도는 일정한 궤도라고 불린다. $I{\displaystyle }$( x${\displaystyle }$) ${\displaystyle I(x)}$에 $t{\displaystyle }$ ${\displaystyle \ne }$ 0 ${\displaystyle t\neq$0}이$$(${\displaystyle 가}$) 있는 경우 일정하지 않은 궤도를 폐쇄 또는 주기라고 한다.

${\displaystyle \mathrm{\phi }}$( ${\displaystyle t}$, ${\displaystyle x}$)${\displaystyle }$= ${\displaystyle x}$ ${\displaystyle \Phi (t,x)=x}$.

리얼 다이내믹 시스템

실제 동적 시스템(R, M, φ)이 주어지면 I(${\displaystyle x_{}^{}}$)는 실제 숫자의 열린 간격, 즉 $I{\displaystyle (}$ x${\displaystyle }$)${\displaystyle }$=${\displaystyle }$( ${\displaystyle {}_{}^{}}$ -${\displaystyle {}_{}^{}}$, ${\displaystyle {}_{}^{}}$ ${\displaystyle x_{}^{}}$+${\displaystyle {}_{}^{}}$) ${\displaystyle I(x)=(t_{x}^{-}^{x}^{x}^{$x}^{+}})이다$.$ M의 임의의 x에 대해

${\displaystyle \property _{x}^{+}:=\\{\Phi (t,x):t\in (0,t_{x}^{+}}\}}}}$

x를 통한 포지티브 세미콜론이라 불린다.

${\displaystyle \gamma _{x}^{-}=\\{\Phi(t,x)):t\in(t_{x}^{-}0)\}}}}}$

x를 통한 마이너스 반감기라고 불린다.

이산 시간 역학 시스템

이산 시간 동적 시스템의 경우:

x의 전방 궤도는 다음과 같다.

${\displaystyle \gamma _{x}^{+}\\\overset {\underset {\mathrm {def}{}}{}}}}}}\{\Phi(t,x):t\geq 0\}}}}}$

x의 역방향 궤도는 다음과 같다.

${\displaystyle \gamma_{x}^-}\\\overset {\underset {\mathrm {def}{}{}}}{{=}\\\\Phi(-t,x):t\geq 0\}}}$

x의 궤도는 다음과 같다.

${\displaystyle \i1}\{x}\{x}\overset {\mathrm {def}{}}}{}}}}\cHB_{x}^ \cup \cup_{x}^{+}}}}}}$

여기서:

• ${\displaystyle \mathrm{\phi }}$ ${\displaystyle \Phi }$은(는) $진화{\displaystyle \mathrm{}}$ 함수${\displaystyle x}$: ${\displaystyle X}$ →$$X {\$displaystyle \Phi :$X$\to$ X$}$이며, 여기서$$ 반복 함수로서,
• 설정 $X{\displaystyle }$ ${\displaystyle X}$은(는) 동적 공간이며
• ${\displaystyle t}$ ${\displaystyle t}$은(는) 반복 횟수로서, ${\displaystyle \mathrm{자연수}}$ $및{\displaystyle }$ t ${\displaystyle \in }$ T ${\displaystyle$ t$\in$ T$}$
• ${\displaystyle x}$ ${\displaystyle x}$은(는) 시스템의 초기 상태이고 x ${\displaystyle \in }$ ${\displaystyle X}$ ${\displaystyle$ x$\in$ X$}$

일반적으로 다른 표기법이 사용된다.

• ${\displaystyle \phi }$( ${\displaystyle t}$, x${\displaystyle }$) ${\displaystyle \Phi (t,x)}$은(는) $\phi {\displaystyle {\mathrm{}}^{}}$ ${\displaystyle t^{}}$( ${\displaystyle x}$) ${\displaystyle \Phi ^{t}(x)}$로 기록됨$$
• ${\displaystyle x_{}}$ ${\displaystyle t_{}}$= ${\displaystyle \phi }$ t${\displaystyle {}^{}}$( x${\displaystyle }$) ${\displaystyle x_{t}=\Phi ^{t}(x)}$ 여기서$$ ${\displaystyle {x\mathrm{}}_{}}$ 0 ${\$은(는) 위의 $표기법$에서 x ${\displaystyle$ x$}$이다.

일반동력계통

일반적인 동적 시스템, 특히 동질 역학에서, 측정 보존 방식으로$$ $확률{\displaystyle }$ 공간 X ${\displaystyle$ X$}$에 작용하는 "nice" $그룹{\displaystyle }$ G$${\$displaystyle G.x\subset$ X$}$을(를) 가진 경우, 스태빌라이저 $S$가 ${\displaystyle {}_{}}$ ${\displaystyle G_{}}$를 ${\displaystyle \mathrm{t하면}}$ $주기적{\displaystyle }$(또는 동등하게 닫힘)으로 불릴 것이다$$.${\displaystyle {}_{}(}$ ${\displaystyle x}$) ${\displaystyle Stab_{G}(x)}$은(는) $G{\displaystyle }$ ${\displaystyle G}$ 내부의 격자다$.$

또한, $설정$된 G${\displaystyle }$. ${\displaystyle x}$ ${\displaystyle G.x}$이(가) X$${\$displaystyle X$ 내부에서 사전 계산된 경우 관련 용어는 경계 궤도다.

궤도의 분류는 다른 수학적 영역과의 관계와 함께 흥미로운 질문으로 이어질 수 있다. 예를 들어, 오펜하임 추측(마굴리스가 증명함)과 리틀우드 추측(부분적으로 린덴스트라우스)은 동질 $우주{\displaystyle }$ S ${\displaystyle 3_{}}$에 대한 어떤 자연 작용의 모든 경계 궤도를 다루고 있는가 하는 문제를 다루고 있다.${\displaystyle SL_{3}(\mathbb {R} )\backslash SL_{3}(\mathbb {Z} )}$ is indeed periodic one, this observation is due to Raghunathan and in different language due to Cassels and Swinnerton-Dyer . Such questions are intimately related to deep measure-classification theorems.

메모들

진화 함수를 이해하여 집단의 원소를 구성할 수 있는 경우가 종종 있는데, 이 경우 집단의 작용의 집단-이성 궤도는 역동적인 궤도와 같은 것이다.

예

• 

  복잡한 2차 다항식을 기반으로 한 이산 동적 시스템의 임계 궤도. 승수=0.99993612384259로 약하게 고정점을 끌어들이는 경향이 있다.

• 

  임계 궤도는 약하게 점들을 끌어들이는 경향이 있다. 수평곡선 밀도가 높은 곳인 고정점(z=0)을 밀어내는 고정점까지 나선형을 볼 수 있다.

• 평형점의 궤도는 일정한 궤도다.

궤도 안정성

궤도의 기본 분류는

• 일정한 궤도 또는 고정점
• 주기 궤도
• 무궤도 및 무궤도 궤도

궤도는 두 가지 방법으로 닫히지 못할 수 있다. 주기적인 궤도로 수렴하면 점증적으로 주기적인 궤도가 될 수 있다. 그러한 궤도는 결코 진정으로 반복되지 않기 때문에 닫히지 않고 임의로 반복 궤도에 가까워진다. 궤도는 또한 혼란스러울 수 있다. 이러한 궤도는 임의로 초기 지점에 근접하지만, 주기적인 궤도로 수렴하는 데 실패한다. 그것들은 초기 조건에 대한 민감한 의존성을 나타내며, 이는 초기 값의 작은 차이가 미래의 궤도에 큰 차이를 일으킬 것이라는 것을 의미한다.

다른 분류를 허용하는 궤도의 다른 특성들이 있다. 근처 지점이 기하급수적으로 빠르게 접근하거나 궤도에서 이탈할 경우 궤도는 쌍곡선이 될 수 있다.

참고 항목

• 방랑 세트
• 위상공간법
• 거미줄 그림 또는 Verhulst 다이어그램
• 복잡한 이차적 매핑 및 궤도 승수의 주기적 지점
• 궤도 초상화

참조

• Hale, Jack K.; Koçak, Hüseyin (1991). "Periodic Orbits". Dynamics and Bifurcations. New York: Springer. pp. 365–388. ISBN 0-387-97141-6.
• Katok, Anatole; Hasselblatt, Boris (1996). Introduction to the modern theory of dynamical systems. Cambridge. ISBN 0-521-57557-5.
• Perko, Lawrence (2001). "Periodic Orbits, Limit Cycles and Separatrix Cycles". Differential Equations and Dynamical Systems (Third ed.). New York: Springer. pp. 202–211. ISBN 0-387-95116-4.