Değişmez

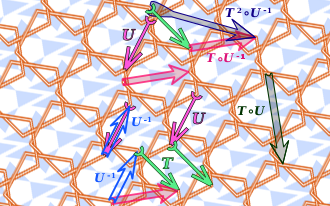
Değişmez, matematikte nesnelere belirli bir türdeki işlemler veya dönüşümler uygulandıktan sonra değişmeden kalan bir matematiksel nesnenin (veya bir matematik nesne sınıfının) özelliğidir.^[1] Belirli nesne sınıfı ve dönüşüm türleri genellikle terimin kullanıldığı bağlam tarafından belirtilir. Örneğin, bir üçgenin alanı Öklid düzleminin izometrilerine göre değişmezdir. Bir denklik bağıntısına göre bir değişmez, her denklik sınıfında sabit olan bir özelliktir.^[2]

Değişmezler, matematiğin geometri, topoloji, cebir ve ayrık matematik gibi çeşitli alanlarında kullanılır. Bazı önemli dönüşüm sınıfları, değişmeden bıraktıkları bir değişmez tarafından tanımlanmaktadır. Örneğin, açıkorur gönderimler, açıları koruyan düzlemin dönüşümleri olarak tanımlanmaktadır. Değişmezlerin keşfi, matematiksel nesnelerin sınıflandırılması sürecinde önemli bir adımdır.^[1]

• Fraleigh, John B. (1976), A First Course In Abstract Algebra, 2nd, Reading: Addison-Wesley, ISBN 0-201-01984-1 
• Herstein, I. N. (1964), Topics In Algebra, Waltham: Blaisdell Publishing Company, ISBN 978-1114541016 
• Kay, David C. (1969), College Geometry, New York: Holt, Rinehart and Winston, LCCN 69-12075 
• McCoy, Neal H. (1968), Introduction To Modern Algebra, Revised Edition, Boston: Allyn and Bacon, LCCN 68-15225 
• J.D. Fokker, H. Zantema, S.D. Swierstra (1991). "Iteratie en invariatie", Programmeren en Correctheid. Academic Service. 90-6233-681-7.
• Eric W. Weisstein, Invariant (MathWorld)
• Popov, V.L. (2001), "Invariant", Hazewinkel, Michiel (Ed.), Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104 

Wikimedia Commons'ta Değişmez ile ilgili ortam dosyaları bulunmaktadır.

• "Applet: Visual Invariants in Sorting Algorithms" 24 Şubat 2022 tarihinde Wayback Machine sitesinde arşivlendi. by William Braynen in 1997