Polynom: Skillnad mellan sidversioner

Ett polynom är ett matematiskt uttryck bestående av icke-negativa heltalspotenser av variabler och konstanter kombinerade genom enbart addition, subtraktion och multiplikation. Uttryckets högsta heltalspotens är polynomets gradtal. Exempelvis är

${\displaystyle x^{2}-4x+5}$

ett andragradspolynom i variabeln ${\displaystyle x}$ medan ${\displaystyle x^{-1}}$ inte är ett polynom överhuvudtaget.

Standardformen för ett polynom av en variabel ${\displaystyle x}$ är

${\displaystyle \sum _{k=0}^{n}a_{k}x^{k}\;=\;a_{n}x^{n}+a_{n-1}x^{n-1}+\ldots +a_{1}x+a_{0}}$

där konstanterna ${\displaystyle a_{k}}$ kallas koefficienter.

Den högsta förekommande exponenten av ${\displaystyle x}$ (här lika med ${\displaystyle n}$ om ${\displaystyle a_{n}\neq 0}$) är polynomets grad. Ofta talar man synonymt om polynomet ${\displaystyle P}$ och den funktion som avbildar ${\displaystyle x}$ på ${\displaystyle P(x)}$.

Enklaste slaget av polynom benämns monom och har endast en term. Ett polynom med två termer kallas för ett binom.

Ett polynom kan också beskrivas som en koefficient multiplicerad med en variabel upphöjd till ett icke-negativt tal. Exempelvis är 2x, 2x + 5, 2x², 1x¹ och 7 alla polynom.

• 
  Andragradspolynom
• 
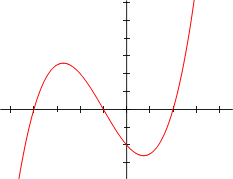
  Tredjegradspolynom
• 
  Fjärdegradspolynom
• 
  Femtegradspolynom

Polynom av grad 0 till 5 benämns ofta enligt följande tabell:

Grad	Benämning	Funktion	Form
0	Nolltegradspolynom (konstant polynom)	Konstant funktion	${\displaystyle a}$
1	Förstagradspolynom (linjärt polynom)	Affin funktion/Linjär funktion	${\displaystyle ax+b}$
2	Andragradspolynom (kvadratiskt polynom)	Kvadratisk funktion	${\displaystyle ax^{2}+bx+c}$
3	Tredjegradspolynom (kubiskt polynom)	Kubisk funktion	${\displaystyle ax^{3}+bx^{2}+cx+d}$
4	Fjärdegradspolynom (kvartiskt polynom)	Kvartisk funktion	${\displaystyle ax^{4}+bx^{3}+cx^{2}+dx+e}$
5	Femtegradspolynom (kvintiskt polynom)	Kvintisk funktion	${\displaystyle ax^{5}+bx^{4}+cx^{3}+dx^{2}+ex+f}$

Det finns ingen enighet om hur graden av nollpolynomet, det vill säga det polynom vars alla koefficienter är 0, skall definieras. Vissa författare föredrar att definiera graden av detta som −1, andra definierar det som −∞; ytterligare andra låter det vara odefinierat.

Ett polynom där högstagradskoefficienten är 1 kallas för moniskt.

Polynom är de enklaste elementära funktionerna. Summor och produkter av polynom är polynom, och även derivator och integraler av polynom är polynom.

En rot eller ett nollställe är ett tal ${\displaystyle r}$ sådant att ${\displaystyle p(r)=0}$. Att hitta rötter till en ekvation eller att lösa en algebraisk ekvation, är ett av matematikens äldsta problem. En del polynom, som exempelvis ${\displaystyle p(x)=x^{2}+1}$, har ingen reell rot. Men genom att utvidga mängden av möjliga nollställen till de komplexa talen, uppnår man att det alltid finns rötter till ett polynom (se Algebrans fundamentalsats). Konjugatet till en imaginär rot är också en rot till ekvationen om alla koefficienter är reella.

Det är intressant att notera att det är försök att lösa ekvationer som starkt bidragit till att införa de olika utvidgningarna av de naturliga talen: för att lösa till exempel ${\displaystyle x+2=0}$ behövs negativa tal, för att lösa ${\displaystyle 3x=5}$ krävs rationella tal, till ${\displaystyle x^{2}-2=0}$ behövs irrationella tal och de komplexa talen behövs för att lösa ${\displaystyle x^{2}+2=0}$.

Ett polynom med grad större eller lika med fem har ingen generell kompletteringsformel (jfr kvadratkomplettera). Det betyder att en polynomekvation av grad större eller lika med fem ofta måste lösas numeriskt.

Ett flertal numeriska metoder för beräkning av nollställen till polynom är kända. Generellt tillämpbara metoder är exempelvis Newtons metod, Laguerres metod och Durand-Kerners metod. Numerisk rotberäkning för polynom kan vara ett illakonditionerat problem och avancerade metoder kan krävas för att hantera polynom med högt gradtal.

Om x = a är ett nollställe till polynomet f(x) innebär detta enligt faktorsatsen att x − a är en delare, och endast då, till polynomet f(x).

Om det rationella talet p/q, där p och q är relativt prima, är ett nollställe till ett polynom ${\displaystyle f(x)=a_{0}+a_{1}x+...+a_{n}x^{n}}$ med heltalskoefficienter så gäller att ${\displaystyle p|a_{0}}$ och ${\displaystyle q|a_{n}}$.^[1]

För att beräkna ett polynomvärde i en viss punkt ${\displaystyle x}$ så evaluerar man lämpligen inte hela uttrycket. Det är effektivare att använda Horners algoritm. Om man skall beräkna polynomvärden för flera likaseparerade punkter så är Newtons differensschema ännu effektivare.

I flervariabelanalys består polynomen av flera variabler. Man säger att totala graden är summan av variablernas maximala potenser i en term. För

${\displaystyle \ p(x,y,z)=2x^{2}yz^{3}-3y^{2}+5yz-2}$

är den totala graden 2 + 1 + 3 = 6.

• Chebyshevpolynom
• Hermitska polynom
• Legendrepolynom
• Multiplicitet
• Polynominterpolation

• Wikimedia Commons har media som rör Polynom.
  Bilder & media
• Slå upp polynom i ordlistan Wiktionary.
  Ordbok