Romb

Romb
Družina	bipiramida
Vrsta	štirikotnik
Stranice in oglišča	4, 4
Grupa simetrije	D2 (*2)
Dualni mnogokotnik	pravokotnik
Značilnosti	konveksni, izotoksalni

Rómb je v ravninski geometriji štirikotnik z vsemi stranicami enake dolžine, oziroma je enakostranični mnogokotnik s štirimi stranicami. Če je kakšen kot v enakostranem štirikotniku pravi, potem so vsi njegovi koti pravi, in takšen štirikotnik je kvadrat, kjer so tudi stranice pravokotne med seboj. V vsakem rombu sta nasprotni stranici vzporedni. Romb je tako poseben primer paralelograma. Romb je paralelogramu to kar je kvadrat pravokotniku. Romb je tudi poseben primer deltoida, štirikotnika z dvema paroma enakih sosednjih stranic. Nasprotni stranici deltoida nista vzporedni dokler deltoid ni tudi romb. Romb je poseben primer romboida, paralelograma z enakima nasprotnima stranicama in enakima nasprotnima kotoma.

Romb v ravnini ima pet prostostnih stopenj: eno za obliko, eno za velikost, eno za usmerjenost in dve za lego.

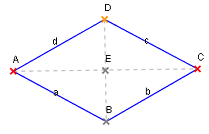
Diagonali v rombu sta druga na drugo pravokotni. Paralelogram je romb, če sta diagonali med seboj pravokotni. S povezavo srednjih točk stranic lahko tvorimo pravokotnik.

Naj so A, B, C in D oglišča romba, označena levosučno. Če je ${\displaystyle {\overrightarrow {AB}}}$ vektor iz A v B, velja:

${\displaystyle {\overrightarrow {AC}}={\overrightarrow {AB}}+{\overrightarrow {BC}}\;,}$

${\displaystyle {\overrightarrow {BD}}={\overrightarrow {BC}}+{\overrightarrow {CD}}={\overrightarrow {BC}}-{\overrightarrow {AB}}\;.}$

Zadnja enakost izhaja iz vzporednosti CD in AB. Notranji produkt je:

${\displaystyle <{\overrightarrow {AC}},{\overrightarrow {BD}}>=<{\overrightarrow {AB}}+{\overrightarrow {BC}},{\overrightarrow {BC}}-{\overrightarrow {AB}}>}$

${\displaystyle =<{\overrightarrow {AB}},{\overrightarrow {BC}}>-<{\overrightarrow {AB}},{\overrightarrow {AB}}>+<{\overrightarrow {BC}},{\overrightarrow {BC}}>-<{\overrightarrow {BC}},{\overrightarrow {AB}}>}$

${\displaystyle =0\;,}$

ker sta normi AB in BC enaki, in ker je notranji produkt bilinearen in simetričen. Notranji produkt diagonal je enak nič, če sta le pravokotni.

• romb ima dve diagonali.
• diagonali romba sta razpolovnici kotov ${\displaystyle \angle ACD=\angle ACB}$, ${\displaystyle \angle DBA=\angle DBC}$ itd.
• vsota kvadratov diagonal je enaka kvadratu stranic, pomnoženemu s 4:

${\displaystyle e^{2}+f^{2}=4a^{2}\!\,.}$

• diagonali se razpolavljata v težišču in velja:

${\displaystyle e=2a\cos {\frac {\alpha }{2}}=2a\sin {\frac {\beta }{2}}\!\,,}$

${\displaystyle f=2a\sin {\frac {\alpha }{2}}=2a\cos {\frac {\beta }{2}}\!\,.}$

• romb ima dve osni simetriji.
• romb je kot deltoid poseben primer tangentnega štirikotnika, ni pa tetivni štirikotnik, saj, če je romb tetivni štirikotnik, je kvadrat. Ima včrtano krožnico s polmerom:

${\displaystyle {\begin{aligned}r&={\frac {a\sin \alpha }{2}}\\&={\frac {ef}{2{\sqrt {e^{2}+f^{2}}}}}\!\,.\end{aligned}}}$

Obseg je skupna dolžina vseh stranic:

${\displaystyle o=4a\!\,.}$

Ploščina romba je enaka polovici produkta dolžin njegovih diagonal:

${\displaystyle p={\frac {ef}{2}}\!\,.}$

Ker je romb tudi paralelogram s štirimi enakimi stranicami, je ploščina enaka dolžini stranice, pomnoženi z višino na to stranico:

${\displaystyle p=av_{a}\!\,.}$

${\displaystyle p=a^{2}\sin \alpha =a^{2}\sin \beta \!\,,}$

kjer je α kot med dvema stranicama v realnem intrervalu (0,π), ${\displaystyle \beta =\pi -\alpha }$.

Ploščina romba je enaka tudi produktu polobsega in polmera včrtane krožnice:

${\displaystyle p=2ar\!\,.}$

Beseda romb izhaja iz grščine za nekaj kar se vrti. Evklid je rabil besedo starogrško ῥόμβος: rómbos - tamburin. Tedaj je moralo biti to glasbilo verjetno romboidne oblike in ne krožne, kot je danes. Njegovi prevajalci menijo, da je beseda izvedena iz grške starogrško ρέμβω: rémbo - vrteti se v krogu. Arhimed je rabil izraz »trdni romb« za dva stožca z isto osnovno ploskvijo. Prva sta besedo »romb« uporabila Heron in Papos Aleksandrijski.

• azteški romb
• romboeder
• romb (znak)

Wikimedijina zbirka ponuja več predstavnostnega gradiva o temi: romb.

• Weisstein, Eric Wolfgang. »Rhombus«. MathWorld.