Izotoksalna oblika
Izotoksalna oblika (tudi robovnoprehodna oblika) je v geometriji simetrija, ki deluje prehodno na robove.
Izraz izvira iz grške besede τοξον, ki pomeni lok
Izotoksalni mnogokotniki
[uredi | uredi kodo]Izotoksalni mnogokotniki so enakostranični mnogokotniki. Vsi enakostranični mnogokotniki pa niso izotoksalni.
V splošnem ima izotoksalni 2n-kotnik diedrsko simetrijo Dn (*n) Zgled: romb je izotoksalni mnogokotnik s simetrijo D2 (*2).
Vsi pravilni mnogokotniki (enakostranični trikotnik, kvadrat,...) so izotoksalni, ki imajo dvojni minimalni red simetrije. Pravilni n-kotnik ima diedrsko simetrijo Dn (*n). Kvadrat je tako izotoksalni mnogokotnik s simetrijo D4 (*4).
| diedrska simetrija | D2 (*2) | D3 (*3) | D4 (*4) | D5 (*5) | |||||
|---|---|---|---|---|---|---|---|---|---|
| ime | romb | enakostranični trikotnik | konkavni šestkotnik | sebe sekajoči šestkotnik | kvadrat | konveksni osemkotnik | pravilni petkotnik | sebe sekajoči (pravilni) pentagram | sebe sekajoči dekagram |
| slika | 
|

|

|
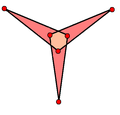
|

|

|

|

|

|
Izotoksalni poliedri in tlakovanja
[uredi | uredi kodo]Izotoksalni poliedri ali tlakovanja morajo biti izogonalni (ogliščnoprehodni) ali izoedrski (prehodne stranske ploskve) ali pa oboje.
 Rombilsko tlakovanje je izotoksalno tlakovanje s simetrijo p6m (*632) . |
Pravilni poliedri so izoedrski, izogonalni in izotoksalni. Kvazipravilni poliedri so izogonalni in izotoksalni, niso pa izoedrski. Njihovi duali so izoedrski in izotoksalni, niso pa izogonalni.
Vsak polieder ali dvorazsežna teselacija, ki nastane iz pravilnega mnogokotnika ni izotaksalen. Zgled: prisekani ikozaeder ima dve vrsti robov: šestkotno-šestkotne in šestkotno-petkotne. Ni možno zaradi simetrije telesa premakniti šestkotno-šestkotnega roba v šestkotno-petkotnega.
Izotoksalni polieder ima enake diedrske kote za vse robove.
Obstaja devet konveksnih izotoksalnih poliedrov nastalih iz platonskih teles, 8 jih je nastalo iz Kepler-Poinsotovih poliedrov. Dodatnih šest je kvazipravilnih (3|p q) zvezdnih poliedrov in njihovih dualov.
Obstoja pet mnogokotniških izotoksalnih tlakovanj evklidske ravnine ter neskončno veliko izotoksalnih mnogokotniških tlakovanj hiperbolične razvnine, vključno z Wythoffovo konstrukcijo pravilna hiperbolična tlakovanja {p, q} .
Glej tudi
[uredi | uredi kodo]