Introduction
The stress-strain curve is a fundamental concept in material science to understand how a material behaves when pulled. With this article, we hope to explain this curve and the different stages that most materials undergo when subjected to a pulling force. Let us begin!
What is the stress-strain curve?
The stress-strain curve refers to a graphical description of stress against strain from the point when there is no load on a material to the point where it breaks under a specific load. The curve’s shape and values help us understand the deformation behaviour of different materials and make a better choice when using them in applications.
But to understand this curve, we must first understand what we mean by the terms ‘stress’ and ‘strain’.
What is Stress (σ)?
Stress can be understood as pressure upon a part. The theoretical definition explains stress as Force/Area. Here, force refers to the pull on the material in Newtons and Area refers to the cross-sectional area perpendicular to the direction of the force.
For example, suppose we place a container with 10 litres of water on a cardboard box of 1 sq. m. area. The weight of the bag produces a compressive stress equal to Mg/A where M is the mass (10 kg), g is the acceleration due to gravity or gravitational pull (~10m/s2), and A is the top area of the cardboard box (1 sq. m).
We calculate the stress in this example as 10*10/1 = 100 N/sq.m. If this stress exceeds what the box can handle, it will collapse. In order for it to not collapse, we must either increase the area of the cardboard box (a bigger box) or reduce the weight.
Let us now suppose we a reduce the water in the container to 1 litres instead. The new stress on the cardboard box becomes 1*10/1 = 10 N/sq.m. The box can handle this stress better than the previous one and therefore, does not collapse anymore.
Another trick is to increase the surface area. If we increase the surface area to 10 times its original surface area but keep the water quantity same as in our first scenario (10 liters), the new stress on the box becomes 10*10/10 = 10 N/sq.m. which is the same as our second example. Since the box did not collapse in our second example, it will not collapse in the third example as well.
The only condition is that the weight should be uniformly distributed. If at any point on the cardboard box, the stress exceeds the maximum permissible limit, it will cause the box to collapse.
The stress always exists in the direction of the load. Therefore the different types of loads lead to corresponding types of stresses. Tensile, compressive, shear, torsional and bending loads create tensile, compressive, shear, torsional and bending stresses respectively.
What Is Strain (ε)?
Strain measures the percentage increase in length when a material is pulled. When we pull a rubber band, it elongates. The ratio of the change in length to the original length of the rubber band gives us the strain on the part.
Strain is a dimensionless number. In this article, we only focus on the longitudinal rain for ease of understanding.
How do we plot the stress-strain curve?
The stress-strain curve is a representation of how much a material deforms upon application of force. To obtain the stress-strain curve, we apply calculated amount of force on a part and measure the change in dimension. We increase the force in steps until the point of fracture. These steps are performed on a special machine known as the Universal Testing Machine (UTM).
Shown above is a Universal Testing Machine. The material is held between the clamps. The bottom clamp is fixed while the upper clamp moves in calibrated steps until the material fractures.
The final result is a set of points that can be plotted on a graph with the force shown as stress (since area is constant) on the Y-axis and the corresponding strain on the X-axis.
Drawing a curve through these set of points gives us the stress-strain curve for that material.

Analysis of the Curve
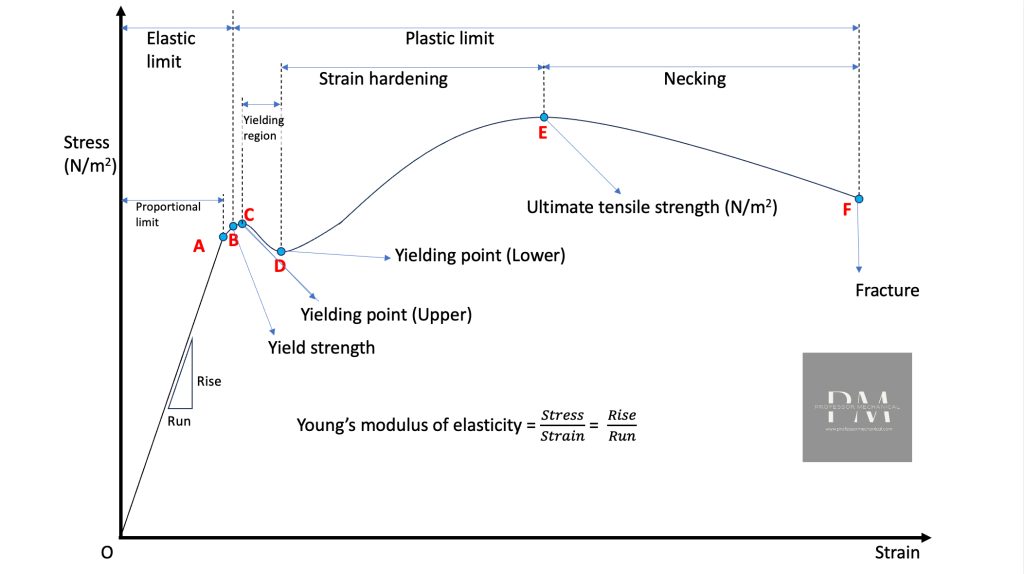
A closer analysis of the stress and strain curve teaches us some very important concepts. Let us note down these important concepts and tackle them one by one.
- Proportional limit / Hooke’s law
- Young’s modulus of elasticity
- Elastic limit
- Yield strength
- Yield point
- Plastic limit
- Strain hardening
- Ultimate tensile strength
- Necking and fracture point
Proportional limit

At the outset, we can see that initially, there is an area where the stress and strain increase linearly. In simple terms, this means that when we double the force on the part, the strain doubles as well.
To clarify further, if a force of 100 N increases the length of the material by 2 mm, a force of 200 N will increase the length by 4 mm and so on.
But this does not happen forever. There comes a point where this pattern breaks. This breaking point for the pattern is known as the proportional limit.
Thus, the proportional limit is the region of the curve where the strain is proportional to the stress. This is also the limit for Hooke’s law. Let’s explore this law further.
Hooke’s law
Hooke’s law is an empirical law (derived through experiments) that states that the amount of force required to extend a spring by a distance increases linearly. Since this is how our material behaves in the proportional limit, we can apply Hooke’s law to our material.
We can simplify the Hooke’s law to apply to our example as follows:
Force ∝ Distance
Since stress ∝ Force ( σ = F/A), and distance is the strain, we can reframe this relationship as
Stress ∝ Strain
Stress = Y x Strain
Stress/Strain = Y (constant)
The constant Y is referred to as the Young’s Modulus of elasticity.
Young’s Modulus of Elasticity
Young’s modulus of elasticity is defined as the ratio of stress and strain. On the stress strain curves, Young’s modulus represents the slope of the stress-strain curve up to the proportional limit. The modulus is an indicator of how willingly a material deforms under a load.
A material that is more flexible will have a lower Young’s modulus of elasticity (Y = Stress/Strain and Strain is more which reduces the value of Y). The slope of the curve will therefore be lower as the material deforms willingly even if the force is small.
On the other hand, a more rigid material will have a higher Young’s modulus of elasticity as more force is required to produce strain, which increases the slope of the curve.
We can understand the comparison better through the following graphic.
Elastic limit

The elastic limit determines the range in which the material retains its elasticity. The material behaves like a rubber band in this section of the curve. You apply a force, you get some elongation. When you remove the force, the material will return to its original length.
The elastic limit extends beyond the proportional limit. This shows that the material is still elastic beyond the proportional limit until the elastic limit. The relationship between stress and strain is no longer proportional but the material will rebound to its original dimensions on the removal of the force.
For metals, the elastic limit does not last very long after the proportional limit. For elastomers such as rubber, the elastic limit can last much longer beyond the proportional limit.
The point where the elastic limit ends is known as the Yield strength. Once the stress on the part increases beyond the yield strength of the material, the material loses elasticity and gains plasticity.
In the plastic region, any deformation caused due to a force remains as it is even after the removal of the force. For some materials such as aluminium, this change does not occur at a specific point but is slowly induced over a range of stresses.
In such cases, the elasticity is not lost at a specific point but over a range of stresses and the material becomes fully plastic and the end of it.
Yield strength

The yield strength is the point on the stress and strain curve where the material loses its elasticity, i.e. the material no longer returns to its original dimensions when we remove the deforming force.
Any dislocations beyond this point become permanent. This is why yield strength is used as the reference point when designing parts for engineering applications.
We must ensure that the parts never endure loads beyond their yield strength for a long and satisfactory service life. If the said application will load the part beyond its yield strength, we can either increase the cross-sectional area of the material or change the material to a more suitable option.
Yielding point
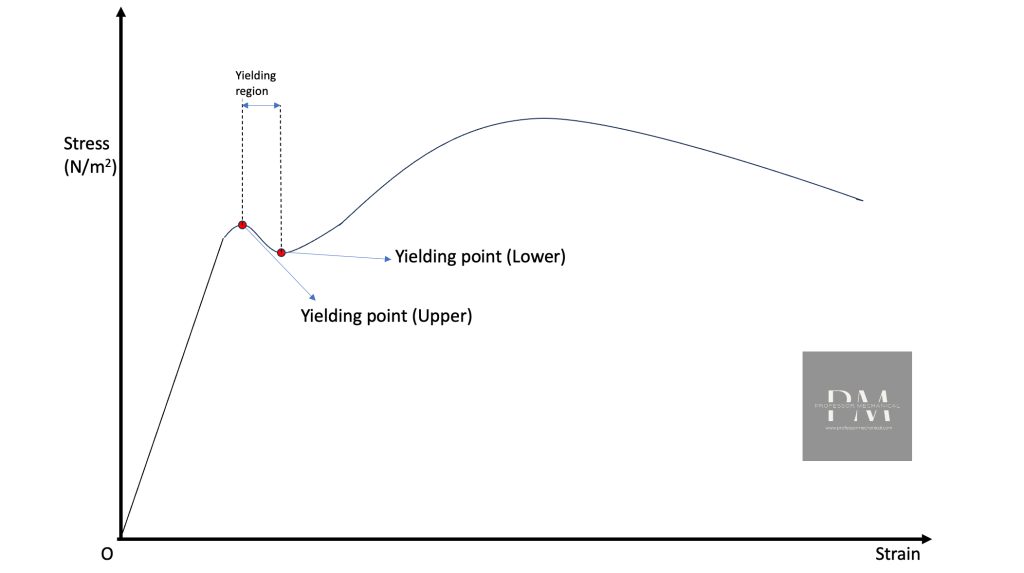
The yielding point is the point where the strain increases at a much higher rate compared to the increase in stress. This is the point on the curve where it begins to flatten, i.e. the slope approaches zero and may also become negative, i.e. the increase in deformation relieves some of the stress and the curve takes a dip.
The region of the curve where this occurs is known as the yielding region. Where the curve takes a dip, the point at the start of the yielding region is known as the Upper Yielding Point and the end point is known as the Lower Yielding point. This is the case for mild steel.
For caution, some parts may even be designed to not approach the lower yielding point stress to reduce the chances of failure.
In cases where the stress and strain curve does not clearly show the yielding point, we designate an Offset Yield Point that may be 0.1% or 0.2% of strain in the material. Then we divide this point by the desired factor of safety for a safe design.
Strain hardening

Strain hardening refers to the hardening of a material through plastic deformation. At the end of the yielding region, the material starts to offer greater resistance to a deforming force. We need to apply more force to increase deformation as the material starts to harden.
The slope of the stress-strain curve begins to rise before it reaches a maximum and then starts to drop again to zero in this region. This rise and fall of the curve’s slope marks the strain hardening region.
This phenomenon is also known as cold work-hardening or cold hardening and is deliberately carried out on some metals to increase their hardness before using them in applications.
Ultimate tensile strength

The ultimate tensile strength is the maximum stress that a material can handle without breaking. Once the material reaches this stress, even a small increase in the applied force will cause the material to start necking and eventually fail.
This point is of special significance as crossing it can lead to a catastrophic failure of the part. At any point during service, we cannot subject the material beyond this point.
For brittle materials, this point is close to the yield point. But when it comes to ductile materials, the ultimate tensile strength is usually significantly higher than the yield point.
Necking and fracture point

Necking is the thinning of the cross sectional area of the material beyond the ultimate tensile strength point. As the stress is increased, the material cannot handle it and it starts to break the bonds at the weakest point of the specimen.
The weakest point undergoes high amount of strain or deformation while there is no appreciable change in the rest of the part.
This causes the material to thin disproportionately at the weakest point and it ultimately breaks when the cross-section is no longer large enough to handle the stress and strain.
The region of the curve this occurs is known as the necking region and the point where the material breaks is known as the fracture point.
Conclusion
The stress and strain diagram is a very important diagram in material science. By analysing the stress strain curves of different materials, we can glean many properties and ascertain their suitability to different applications.
We hope that this article gave you a brief overview of the entire stress strain curve and why it is so important to material scientists.
