Cifras arábigas

Las cifras arábigas son los diez símbolos básicos empleados para expresar números en la mayor parte del mundo siguiendo las normas del sistema de numeración indo-arábigo. No obstante, las cifras arábigas también sirven para expresar números en otros sistemas como la numeración octal o la hexadecimal. De forma coloquial estas diez cifras son denominadas números arábigos pero esto no es totalmente correcto: un número es una cantidad abstracta y universal mientras que una cifra es el símbolo escrito que se usa para expresar un número.

La razón por la que los dígitos se conocen más comúnmente como "números arábigos" en Europa y América es que fueron introducidos en Europa en el siglo X por hablantes de árabe de España y norte de África, que entonces usaban los dígitos desde Libia hasta Marruecos. En la parte oriental de la Península arábiga, los árabes usaban los números arábigos orientales o números "mashrikíes": ٠ ١ ٢ ٣ ٤ ٥ ٦ ٧ ٨ ٩

Al-Nasawi escribió a principios del siglo XI que los matemáticos no se habían puesto de acuerdo aún sobre la forma de los números, pero la mayoría había accedido a entrenarse con las formas ahora conocidas como números arábigos orientales.^[1]​ Los especímenes más antiguos de cifras disponibles son de Egipto y datan de 873–874 EC. Muestran tres formas del número "2" y dos formas del número "3", y estas variaciones indican la divergencia entre lo que más tarde se conoció como los números arábigos orientales y los números arábigos occidentales.^[2]​ Los números arábigos occidentales comenzaron a utilizarse en el Magreb y Al-Ándalus a partir del siglo X.^[3]​

Los cálculos se realizaron originalmente utilizando un tablero de polvo (takht, latín: tabula), que implicaba escribir símbolos con un punzón y borrarlos. El uso del tablero de polvo también parece haber introducido una divergencia en la terminología: mientras que el cómputo hindú se llamaba ḥisāb al-hindī en el este, se llamaba ḥisāb al-ghubār en el oeste (literalmente, "cálculo con polvo").^[4]​ Los propios números se denominaban en occidente ashkāl al‐ghubār ("figuras de polvo") o qalam al-ghubår ("letras de polvo").^[5]​ Al-Uqlidisi más tarde inventó un sistema de cálculos con tinta y papel "sin tablero y borrado" (bi-ghayr takht wa-lā maḥw bal bi-dawāt wa-qirṭās).^[6]​

Las primeras menciones de los numerales en Occidente se encuentran en el Codex Vigilanus (o Albeldensis) de 976.^[7]​

Desde la década de 980, Gerberto de Aurillac (más tarde, el Papa Silvestre II) usó su cargo para difundir el conocimiento de los números en Europa. Gerbert estudió en Barcelona en su juventud. Se sabe que solicitó tratados matemáticos sobre el astrolabio a Lupitus de Barcelona después de su regreso a Francia.

Leonardo Fibonacci (también conocido como Leonardo de Pisa), un matemático nacido en la República de Pisa que había estudiado en Bugía (Bougie), Argelia, promovió el sistema numérico indio en Europa con su libro de 1202 Liber Abaci.

Fray Bernardino de Sahagún, en su Códice Florentino, también conocido como Historia general de las cosas de Nueva España. documentó la cultura de la civilización mexica. Los "colegiales", jóvenes mexicanos trilingües (escribían en latín, náhuatl y español), aprendieron a usar el alfabeto latino para escribir en náhuatl. Sobre todo, aprendieron a usar los números indoarábigos en vez de los números romanos, que aún se usaban en España. En el texto de Sahagún, no aparece ningún número romano. Martín de la Cruz y Juan Badiano, autores del Manual de hierbas medicinales de las Indias, también conocido como Códice de la Cruz-Badiano, de 1552, también utilizaron únicamente las cifras arábigas y no los números romanos.^[8]​

El glifo que se usa hoy en día en el mundo occidental para representar el número 1, una línea horizontal, a menudo con una serifa en la parte superior y, a veces, una línea horizontal corta en la parte inferior, se remonta a la escritura bráhmica de la antigua India, donde se usaba una simple línea horizontal. Se transmitió a Europa a través del Magreb y Al-Ándalus durante la Edad Media, a través de obras eruditas escritas en árabe.

El dígito utilizado en el mundo occidental moderno para representar el número 2 se remonta a la escritura índica brahmica, donde "2" se escribía como dos líneas horizontales. En chino y japonés modernos (y en hanja coreano) todavía usan este método. La escritura gupta giró las dos líneas 45 grados, haciéndolos diagonales. La línea superior a veces también se acortaba y su extremo inferior se curvaba hacia el centro de la línea inferior. En la escritura de Nagari, la línea superior se escribía más como una curva que conectaba con la línea inferior. En la escritura árabe ghubar, la línea inferior era completamente vertical y el dígito parecía un signo de interrogación final sin puntos. Restaurar la línea inferior a su posición horizontal original, pero manteniendo la línea superior como una curva que se conecta a la línea inferior conduce a nuestro dígito moderno.^[9]​

El uso de tres líneas para denotar el número 3 ocurría en muchos sistemas de escritura, incluidos algunos (como los números romanos y chinos) que todavía están en uso. Esa fue también la representación original de 3 en la notación numérica brahmica (india), con sus primeras formas alineadas verticalmente.^[10]​ Sin embargo, durante el Imperio Gupta, el signo se modificó mediante la adición de una curva en cada línea. La escritura nāgarī giraba las líneas en el sentido de las agujas del reloj, de modo que aparecían horizontalmente, y terminaba cada línea con un trazo corto hacia abajo a la derecha. En escritura cursiva, los tres trazos finalmente se conectaron para formar un glifo parecido a un ⟨3⟩ con un trazo adicional en la parte inferior: ३.

Los dígitos indios se extendieron al Califato en el siglo IX. El trazo inferior se eliminó alrededor del siglo X en las partes occidentales del califato, como el Magreb y al-Ándalus, cuando se desarrolló una variante distinta ("árabe occidental") de los símbolos de dígitos, incluido el 3 occidental moderno. Por el contrario, los árabes orientales conservaron y ampliaron ese trazo, girando el dígito una vez más para producir el dígito árabe moderno ("oriental") "٣".^[11]​

Los números brahmi representaban 1, 2 y 3 con esa cantidad de líneas. El 4 se simplificó uniendo sus cuatro líneas en una cruz que se parece al signo de sumar moderno. La escritura shunga agregaría una línea horizontal encima del dígito, y la kshatrapa y pallava evolucionaron el dígito hasta un punto en el que la velocidad de escritura era una preocupación secundaria. El 4 árabe todavía tenían el concepto primitivo de la cruz, pero en aras de la eficiencia, se hizo de un solo golpe conectando el extremo "oeste" con el extremo "norte"; el extremo "este" estaba rematado con una curva. Los europeos abandonaron la curva final y gradualmente hicieron que el dígito fuera menos cursivo, terminando con un dígito muy cercano a la cruz brahmán original.^[12]​

La evolución del dígito occidental moderno para el número 5 no se remonta al sistema indio, como para los dígitos del 1 al 4. Los imperios Kushana y Gupta en lo que ahora es India tenían entre ellos varias formas diferentes que no se parecen al dígito moderno. Los nagari y punjabi tomaron estos dígitos y todos crearon formas que eran similares a una "h" minúscula girada 180°. Los árabes ghubar transformaron el dígito de varias maneras diferentes, produciendo a partir de que eran más similares a los dígitos 4 o 3 que a 5.^[13]​ Fue a partir de estas cifras que los europeos finalmente crearon el 5 moderno.

La evolución de nuestro moderno dígito 6 parece bastante simple en comparación con los otros dígitos. El 6 moderno se remonta a los números brahmi de la India, que se conocen por primera vez a partir de los Edictos de Ashoka alrededor del año 250 a.^[14]​^[15]​^[16]​^[17]​ Estaba escrito de un solo trazo como una letra E minúscula cursiva y girada 90 grados en el sentido de las agujas del reloj. Gradualmente, la parte superior del trazo (sobre el garabato central) se volvió más curva, mientras que la parte inferior del trazo (debajo del garabato central) se volvió más recta. Los árabes eliminaron la parte del trazo debajo del garabato. A partir de ahí, la evolución europea a nuestro 6 moderno fue muy sencilla, excepto algunas formas que se parecían más a una G mayúscula.^[18]​

Al principio, los indios escribían el 7 más o menos de un solo trazo como una curva que parece una ⟨J⟩ mayúscula invertida verticalmente. La principal contribución de los árabes ghubar occidentales fue hacer que la línea más larga fuera diagonal en lugar de recta, aunque mostraron algunas tendencias a hacer que el dígito fuera más rectilíneo. Los árabes orientales desarrollaron el dígito de una forma que se parecía a nuestro 6 a una que parecía una V mayúscula. Ambas formas árabes modernas influyeron en la forma europea de dos trazos que consta de un trazo superior horizontal unido a su derecha a un trazo que desciende hasta la esquina inferior izquierda, una línea ligeramente curva en algunas variantes de fuente. Como es el caso con el dígito europeo, el dígito cham y jemer para 7 también evolucionó para parecerse a su dígito 1, aunque de una manera diferente, por lo que también les preocupaba hacer que su 7 fuera más diferente. Para los jemeres, esto a menudo implicaba agregar una línea horizontal en la parte superior del dígito.^[19]​ Esto es análogo al trazo horizontal a través de la mitad que a veces se usa en la escritura a mano en el mundo occidental, pero que casi nunca se usa en fuentes digitales. Sin embargo, este trazo horizontal es importante para distinguir el glifo de siete del glifo de uno en la escritura que usa un trazo largo hacia arriba en el glifo de 1. En algunos dialectos griegos de principios del siglo XII, la línea diagonal más larga se dibujó en una línea transversal más bien semicircular.

El dígito moderno 8, como todos los números arábigos modernos distintos del cero, se origina con los números brahmi. El dígito brahmi para ocho en el siglo I se escribió de un solo trazo como una curva └┐ que parecía una H mayúscula con la mitad inferior de la línea izquierda y la mitad superior de la línea derecha eliminadas. Sin embargo, el dígito para ocho utilizado en la India en los primeros siglos de la era común desarrolló una variación gráfica considerable y, en algunos casos, tomó la forma de una sola cuña, que se adoptó en la tradición perso-árabe como ٨ (y también dio lugar a la forma posterior devanagari ८); el glifo curvo alternativo también existía como una variante en la tradición perso-árabe, donde llegó a parecerse a nuestro dígito 5. 

Los dígitos, tal como se usaban en al-Ándalus en el siglo X, eran una variante occidental distintiva de los glifos utilizados en el mundo de habla árabe, conocidos como números ghubār (ghubār que se traduce como "mesa de arena"). En estos dígitos, la línea del glifo similar a 5 utilizado en los manuscritos indios para ocho se formó en ghubār como un bucle cerrado, que fue la forma de 8 que se adoptó en el uso europeo en el siglo X.^[20]​

En las primeras formas, los indios escribieron un dígito 9 de forma similar al signo de interrogación de cierre moderno sin el punto inferior. Las escrituras kshatrapa, andhra y gupta comenzaron a curvar la línea vertical inferior y salieron con un aspecto similar a 3. La nagari continuó el trazo inferior para hacer un círculo y encerrar el 3 similar, de la misma manera que el signo @ rodea una a minúscula. A medida que pasaba el tiempo, el círculo envolvente se hizo más grande y su línea continuó más allá del círculo hacia abajo, a medida que lo que quedaba del cuasi 3 se hacía más pequeño. Pronto, todo lo que quedó del 3 pequeño era un garabato. Los árabes simplemente conectaron ese garabato con el trazo descendente en el medio y el cambio europeo posterior fue puramente cosmético.

Los antiguos griegos no tenían ningún símbolo para el cero (μηδέν) y no usaban un marcador de posición de dígito para él.^[21]​ Según el matemático Charles Seife, los antiguos griegos comenzaron a adoptar el marcador de posición babilónico cero para su trabajo en astronomía después del 500 a. C., representándolo con la letra griega minúscula ό ( όμικρον) u omicron.^[22]​ Sin embargo, después de usar el marcador de posición cero babilónico para cálculos astronómicos, normalmente convertían los números nuevamente en números griegos.^[22]​ Los griegos parecían tener una oposición filosófica al uso del cero como número.^[22]​ Otros eruditos dan a la adopción parcial griega del cero babilónico una fecha posterior, con el científico Andreas Nieder dando una fecha posterior al 400 a. C. y el matemático Robert Kaplan datando después de las conquistas de Alejandro.^[23]​^[24]​

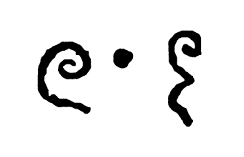
Un punto negro se usaba como marcador de posición decimal en el manuscrito Bakhshali, partes del cual datan del 224 al 383 d. C.^[25]​

Hay numerosas inscripciones en planchas de cobre, como una o minúscula, algunas de ellas posiblemente fechadas en el siglo VI, aunque su fecha o autenticidad está abiertas a dudas.^[26]​

(Una tablilla de piedra encontrada en las ruinas de un templo cerca de Sambor en el MekongKratié, Camboya, incluye la inscripción "605" en números jemeres (un conjunto de glifos numéricos para el sistema numérico hindú-árabe). El número es el año de la inscripción en la era Saka, correspondiente a una fecha del 683 d. C.^[27]​

El primer uso conocido de glifos especiales para los dígitos decimales que incluye la aparición indudable de un símbolo para el dígito cero, un pequeño círculo, aparece en una inscripción de piedra encontrada en el Templo Chaturbhuj, Gwalior, en India, fechada en 876.^[28]​^[29]​