Matemáticas/Historia/Texto completo
Matemáticas - Historia
[editar]Si estás buscando la respuesta a la pregunta ¿Quien inventó los números?, después de leer este artículo verás que no existe una respuesta única ni tampoco clara.
¿Es más antigua la escritura que la numeración? No hay evidencia documental de escritura hasta el 2200 a.C. De esa fecha son las tablillas de barro cocido halladas en las ciudades babilónicas de Susa y Uruk, hoy la ciudad iraquí de Warka.
El primer atisbo de número, lo encontramos en la prehistoria. Una marca en un hueso, representaba al número 1 (un animal cazado). Surgió debido a la necesidad práctica de contar objetos.
Pero fueron los sumerios los que decidieron darle al número 1 su independencia. Lo lideraron, representándolo cómo una ficha (un pequeño cono). Podemos decir si miedo a equivocarnos, que esta pequeña ficha, cambió el curso de la historia.
En un hueso o un palo sólo se podía añadir (sumar), pero con el uso de estos conos, también se podía restar … Habían inventado la aritmética!!
En el cuarto milenio antes de Cristo, en Mesopotamia donde abundaba la arcilla, unos pequeños guijarros representan cantidades numéricas. De esta forma podían contabilizar sacos de trigo ó de cabezas de ganado.
Entonces en las ciudades, era necesario almacenar y repartir el grano. Tenían que averiguar cuánto le tocaba a cada uno y esto requería de la aritmética. Podemos atribuir el invento de las matemáticas a la vida urbana.
El conteo se debió iniciar mediante el uso de objetos físicos (tales como montones de piedras) y de marcas de cuenta, como las encontradas en huesos tallados: el de Lebombo, con 29 muescas grabadas en un hueso de babuino, tiene unos 37.000 años de antigüedad y otro hueso de lobo encontrado en la antigua Checoslovaquia, con 57 marcas dispuestas en cinco grupos de 11 y dos sueltas, se ha estimado en unos 30.000 años de antigüedad. Ambos casos constituyen una de las más antiguas marcas de cuenta conocidas habiéndose sugerido que pudieran estar relacionadas con registros de fases lunares.3 En cuanto al origen ordinal algunas teorías lo sitúan en rituales religiosos. Los sistemas numerales de la mayoría de familias lingüísticas reflejan que la operación de contar estuvo asociado al conteo de dedos (razón por la cual los sistemas de base decimal y vigesimal son los más abundantes), aunque están testimoniado el empleo de otras bases numéricas además de 10 y 20.
Historia del concepto de número
[editar]Cognitivamente el concepto de número está asociado a la habilidad de contar y comparar cual de dos conjuntos de entidades similares tiene mayor cantidad de elementos. Las primeras sociedades humanas se toparon muy pronto con el problema de determinar cual de dos conjuntos era "mayor" que otro, o de conocer con precisión cuantos elementos formaban una colección de cosas. Esos problemas podían ser resueltos simplemente contando. La habilidad de contar del ser humano, no es un fenómeno simple, aunque la mayoría de culturas tienen sistemas de cuenta que llegan como mínimo a centenares, algunos pueblos con una cultura material simple, sólo disponen de términos para los números 1, 2 y 3 y usualmente usan el término "muchos" para cantidades mayores, aunque cuando es necesario usan recursivamente expresiones traducibles como "3 más 3 y otros 3" cuando es necesario.
El conteo se debió iniciar mediante el uso de objetos físicos (tales como montones de piedras) y de marcas de cuenta, como las encontradas en huesos tallados: el de Lebombo, con 29 muescas grabadas en un hueso de babuino, tiene unos 37.000 años de antigüedad y otro hueso de lobo encontrado en la antigua Checoslovaquia, con 57 marcas dispuestas en cinco grupos de 11 y dos sueltas, se ha estimado en unos 30.000 años de antigüedad. Ambos casos constituyen una de las más antiguas marcas de cuenta conocidas habiéndose sugerido que pudieran estar relacionadas con registros de fases lunares.[1] En cuanto al origen ordinal algunas teorías lo sitúan en rituales religiosos. Los sistemas numerales de la mayoría de familias lingüísticas reflejan que la operación de contar estuvo asociado al conteo de dedos (razón por la cual los sistemas de base decimal y vigesimal son los más abundantes), aunque están testimoniado el empleo de otras bases numéricas además de 10 y 20.
El paso hacia los símbolos numerales, al igual que la escritura, se ha asociado a la aparición de sociedades complejas con instituciones centralizadas constituyendo artificios burocráticos de contabilidad en registros impositivos y de propiedades. Su origen estaría en primitivos símbolos con diferentes formas para el recuento de diferentes tipos de bienes como los que se han encontrado en Mesopotamia inscritos en tablillas de arcilla que a su vez habían venido a sustituir progresivamente el conteo de diferentes bienes mediante fichas de arcilla (constatadas al menos desde el 8000 a. C.) Los símbolos numerales más antiguos encontrados se sitúan en las civilizaciones mesopotámicas usándose como sistema de numeración ya no solo para la contabilidad o el comercio sino también para la agrimensura o la astronomía como, por ejemplo, registros de movimientos planetarios.[2]
En conjunto, desde hace 5.000 años la mayoría de las civilizaciones han contado como lo hacemos hoy aunque la forma de escribir los números (si bien todos representan con exactitud los naturales) ha sido muy diversa. Básicamente la podemos clasificar en tres categorías:
- Sistemas de notación aditiva. Acumulan los símbolos de todas las unidades, decenas, centenas,... necesarios hasta completar el número. Aunque los símbolos pueden ir en cualquier orden, adoptaron siempre una determinada posición (de más a menos). De este tipo son los sistemas de numeración: Numeración egipcia, hitita, cretense, romano, griego, armenio y judío.
- Sistemas de notación híbrida. Combinan el principio aditivo con el multiplicativo. En los anteriores 500 se representa con 5 símbolos de 100, en éstos se utiliza la combinación del 5 y el 100. El orden de las cifras es ahora fundamental (estamos a un paso del sistema posicional). De este tipo son los sistemas de numeración: Chino clásico, asirio, armenio, etíope y maya. Este último utilizaba símbolos para el "1", el "5" y el "0". Siendo este el primer uso documentado del cero tal como lo conocemos hoy (Año 36 a.C) ya que el de los babilonios solo se utilizaba entre otros dígitos.
- Sistemas de notación posicional. La posición de las cifras nos indica si son unidades, decenas, centenas,... o en general la potencia de la base. Solo tres culturas además de la india lograron desarrollar un sistema de este tipo: El sistema Chino (300 a. C.) que no disponía de 0, el sistema Babilónico (2000 a. C.) con dos símbolos, de base 10 aditivo hasta el 60 y posicional (de base 60) en adelante, sin "0" hasta el 300 a. C.
Creación del cero
[editar]En cualquier sistema de numeración posicional surge el problema de la falta de unidades de determinado orden. Por ejemplo, en el sistema babilónico el número escrito en base 60 puede ser ó . A veces, se utilizaba la posición vacía para evitar este problema 3 _ 2; pero los escribas debían tener mucho cuidado para no equivocarse.
Hacia el siglo III a. C., en Grecia, se comenzó a representar la nada mediante una "o" que significa oudos 'vacío', y que no dio origen al concepto de cero como existe hoy en día. La idea del cero como concepto matemático parece haber surgido en la India mucho antes que en ningún otro lugar. La única notación ordinal del viejo mundo fue la sumeria, donde el cero se representaba por un vacío.
En América, la primera expresión conocida del sistema de numeración vigesimal prehispánico data del siglo III a. C. Se trata de una estela olmeca tardía, la cual ya contaba tanto con el concepto de "orden" como el de "cero". Los mayas inventaron cuatro signos para el cero; los principales eran: el corte de un caracol para el cero matemático, y una flor para el cero calendárico (que implicaba, no la ausencia de cantidad, sino el cumplimiento de un ciclo).
Números negativos
[editar]Brahmagupta, en el 628 de nuestra era, considera las dos raíces de las ecuaciones cuadráticas, aunque una de ellas sea negativa o irracional. De hecho en su obra es la primera vez que aparece sistematizada la aritmética (+, -, *, / , potencias y raíces) de los números positivos, negativos y el cero, que él llamaba los bienes, las deudas y la nada. Así, por ejemplo, para el cociente, establece:
Positivo dividido por positivo, o negativo dividido por negativo, es afirmativo. Cifra dividido por cifra es nada (0/0=0). Positivo dividido por negativo es negativo. Negativo dividido por afirmativo es negativo. Positivo o negativo dividido por cifra es una fracción que la tiene por denominador (a/0=¿?)
No solo utilizó los negativos en los cálculos, sino que los consideró como entidades aisladas, sin hacer referencia a la geometría. Todo esto se consiguió gracias a su despreocupación por el rigor y la fundamentación lógica, y su mezcla de lo práctico con lo formal.
Sin embargo el tratamiento que hicieron de los negativos cayó en el vacío, y fue necesario que transcurrieran varios siglos (hasta el Renacimiento) para que fuese recuperado.
Al parecer los chinos también poseían la idea de número negativo, y estaban acostumbrados a calcular con ellos utilizando varillas negras para los negativos y rojas para los positivos.
Descubrimiento de los inconmensurables
[editar]Las circunstancias y la fecha de este descubrimiento son inciertas, aunque se atribuye a la escuela pitagórica (se utiliza el Teorema de Pitágoras). Aristóteles menciona una demostración de la inconmensurabilidad de la diagonal de un cuadrado con respecto a su lado basada en la distinción entre lo par y lo impar. La reconstrucción que realiza C. Boyer es:
Sean d:diagonal, s:lado y d/s racional que podremos escribirlo como con p y q primos entre sí. Por el teorema de Pitágoras tenemos que , , entonces y por tanto debe ser par y también p, y por tanto q impar. Al ser p par tenemos , entonces y , entonces es par y q también, entonces q es par e impar con lo que tenemos una contradicción.
La teoría pitagórica de todo es número quedó seriamente dañada.
El problema lo resolvería Eudoxo de Cnido (408-355 a. C.) tal como nos indica Euclides en el libro V de Los elementos. Para ello estableció el Axioma de Arquímedes: Dos magnitudes tienen una razón si se puede encontrar un múltiplo de una de ellas que supere a la otra (excluye el 0). Después en la Definición-5 da la famosa formulación de Eudoxo: Dos magnitudes están en la misma razón si dados dos números naturales cualesquiera m y n, si entonces (definición que intercambiando el 2º y 3º términos equivale a nuestro procedimiento actual).
En el libro de J.P. Colette se hace la observación de que esta definición está muy próxima a la de número real que dará [[Richard Dedekind|Dedekind en el siglo XIX, divide las fracciones en las tales que y las que no. El hombre neolítico ya hacía matemática elemental, por lo tanto sabía sumar; pero previamente captó la idea de restar, puesto que sus medios de subsistencia disminuían durante el año, y no le era tan fácil de reponer.
Los egipcios llegaron a sumar lo que se llaman hoy, números naturales y los números fraccionarios. Los babilonios llegaron a sumar los cuadrados de los números naturales. Los chinos y los hindúes sumaron números negativos. En el Renacimiento, con el auge de la banca y del comercio, se impuso la suma de decimales, catapultada por el uso del sistema de numeración decimal. Además se popularizó la adición de logaritmos vulgares, que reemplazaba eficazmente a la multiplicación de números tanto en el comercio, finanzas, astronomía, navegación, etc.
Los signos + (suma) y – (resta). La primera vez que aparecen los signos + (más) y – (menos) en un libro impreso, que se sepa hoy en día, es en la obra Mercantile Arithmetic, o Behende und hubsche Rechenung au allen Kau manscha, del matemático alemán Johannes Widman (1462 – 1498), publicado en Leipzig en 1489. Sin embargo, Widman no utiliza los signos + y – como símbolos de las operaciones aritméticas suma y resta, sino, dentro de las prácticas comerciales analizadas en el texto, para expresar exceso y defecto de las mercancías, por ejemplo, en el peso de los barriles. En la siguiente imagen vemos “4 + 5” que quiere decir “4 centner + 5 pfund” o “5 – 17” expresando “5 centner – 17 pfund”, donde recordemos que el “centner” y el “pfund” son unidades de peso alemanes, que 1 “centner” son 100 “pfund”, y un “centner” equivale a 50 kilogramos.
Primer uso de los signos + y – impresos en el libro Mercantile Arithmetic (1489), de Johannes Widman Primer uso de los signos + y – impresos en el libro “Mercantile Arithmetic” (1489), de Johannes Widman
Se suele citar el libro de aritmética del matemático holandés Van der Hoeke (siglo XVI) como la primera publicación impresa en la que aparecen los signos + y – como operaciones algebraicas, ya que se suele fechar su publicación en 1514, sin embargo, esta es de 1937 (la fecha de 1514 es un error relacionado con la edición de 1944). Como menciona Florian Cajori, la primera publicación impresa con el significado algebraico de estos signos es el libro de álgebra y aritmética Ayn new Kunstlich Beuch (1518), del matemático alemán Henricus Grammateus (aprox. 1492-1525).
Sin embargo, esta no es la primera aparición de los signos + y –, ya que se pueden encontrar en algunos manuscritos de Alemania, escritos en latín y en alemán, de los últimos veinte años del siglo XV. En la Biblioteca de Dresde existe un volumen de manuscritos (el MS C80) en los que aparecen, quizás por primera vez, los signos + y –. Manuscritos a los que tuvieron acceso tanto Widman, como Grammateus.
Signos más y menos, que aparecen en dos expresiones algebraicas, en dos hojas de los manuscritos latinos MS C80, páginas 350 y 352, de la Biblioteca de Dresde, del año 1486 Signos más y menos, que aparecen en dos expresiones algebraicas, en dos hojas de los manuscritos latinos MS C80, páginas 350 y 352, de la Biblioteca de Dresde, del año 1486
La forma del signo más como una cruz + se debe a que originalmente en los manuscritos latinos se utilizaba la conjunción latina “et”, es decir, la conjunción “y”, para expresar la adición, de la misma forma que nosotros seguimos diciendo hoy en día “2 y 2 son 4”. El signo + es una abreviatura de “et”, de hecho, algunos estudiosos han enumerado más de cien abreviaturas distintas de la palabra “et” en textos latinos, y una de ellas sería la cruz + (pensemos en la escritura de la t). En uno de esos primeros manuscritos, de 1417, aparece una cruz +, pero con el segmento vertical inclinado hacia atrás.
La primera vez que aparece el signo + en un manuscrito podría ser la obra Algorismus proportionum del matemático Nicolás de Oresme (1323-1382), escrito entre los años 1356 y 1361. Sin embargo, es posible también que este signo + haya sido escrito por un copista posterior y no estuviese en la obra original.
El origen del signo – es más incierto, y existen diferentes teorías que tratan de explicarlo. Una de ellas es que podría venir de la utilización de la barra horizontal que los mercaderes utilizaban para indicar la separación de la tara, llamada durante mucho tiempo “minus”, del peso total de una mercancía, es decir, el peso del recipiente del producto. También, podría ser una contracción de la abreviación \overline{m} de la palabra “minus”. Según otra teoría, podría derivar del signo utilizado por el matemático griego Diofanto de Alejandría (siglo III) para el menos, que originalmente era una psi \Psi invertida con la parte de arriba recortada, algo así como una cuña como esta \wedge , pero con una línea vertical en medio de las dos laterales, que habría derivado a una especie de t mayúscula \top , que al perder el pie se quedó en el signo –. También podría venir de un símbolo hierático egipcio.
Antes del siglo XV se utilizaron en Italia, como en otros sitios, las palabras más y menos en el idioma de escritura (en latín, “plus” para más y “minus” para menos), de ahí derivaron, por abreviatura las letras “p” y “m” (o estas con una tilde \widetilde{p}, \widetilde{m} o un segmento encima \overline{p}, \overline{m} ) para designar la suma y la resta. Estas abreviaturas, \widetilde{p}, \widetilde{m} , aparecen por primera vez en la obra “Summa de arithmetica, geometria, proportioni et proportionalita” (1494), del matemático italiano Luca Pacioli (1447-1517), y se siguieron utilizando en los siglo XV y XVI. Los signos alemanes + y – empezaron a utilizarse en Italia ya en el siglo XVII.
Página de la obra Summa de arithmetica (1494), de Luca Pacioli, en la que aparecen por primera vez los signos <img src='http://s0.wp.com/latex.php?latex=%5Cwidetilde%7Bp%7D%2C+%5Cwidetilde%7Bm%7D++&bg=T&fg=000000&s=0' alt='\widetilde{p}, \widetilde{m} ' title='\widetilde{p}, \widetilde{m} ' class='latex' />, para representar suma y resta. En esta página vemos también la regla del signo en la multiplicación “más por más siempre es más, menos por menos siempre es más,…” (además, “più” es más y “meno” es menos en italiano) Página de la obra Summa de arithmetica (1494), de Luca Pacioli, en la que aparecen por primera vez los signos [latex]\widetilde{p}, \widetilde{m} [/latex], para representar suma y resta. En esta página vemos también la regla del signo en la multiplicación “más por más siempre es más, menos por menos siempre es más,…” (además, “più” es más y “meno” es menos en italiano)
El primer uso de los signos + y – en Gran Bretaña fue en 1557 en el libro The Whetstone of Witte, en el que apareció por primera vez el símbolo = para la igualdad. En España y Francia se utilizaban tanto los símbolos alemanes + y –, como los símbolos italianos “p” y “m”.
La cruz + para el símbolo de la suma tuvo también diferentes formas. Por supuesto, la forma principal ha sido la cruz griega, que es la que seguimos utilizando hoy en día. También se utilizó la cruz latina, aunque más frecuentemente utilizada en horizontal (con la parte alargada a la derecha o a la izquierda). Aunque menos, también se utilizaron la cruz que en Escandinavia se llama de San Jorge o la variación de esta que es la cruz de Malta.
Diferentes tipos de cruces que se utilizaron para el signo de la adición. La cruz griega, la cruz latina, la cruz de San Jorge y la cruz de Malta Diferentes tipos de cruces que se utilizaron para el signo de la adición. La cruz griega, la cruz latina, la cruz de San Jorge y la cruz de Malta
A pesar de la sencillez del signo – para la resta, cierto grupo de matemáticos lo sustituyó por el signo más complejo ÷, que fue utilizado durante unos cuatrocientos años, incluso con algunas variaciones, como tener solo el punto de arriba. También se utilizó como signo menos, dos barras seguidas “– –” o tres barras “– – –”.
Por supuesto, antes de estos signos se utilizaron otros para expresar la suma y la resta. Por ejemplo, los babilonios tenían un ideograma en la escritura cuneiforme para la adición (“tab”, que era una cuña-triángulo isósceles- con la punta hacia abajo) y otro para la sustracción (“lal”, una cuña con la punta hacia la derecha). O en el papiro egipcio de Ahmes se utilizan dos piernas caminando hacia delante para el más, y caminando hacia atrás para el menos.
Problema 28 del Papiro de Ahmes –o Papiro matemático Rhind- en el que aparece el signo de la suma como dos piernas caminando hacia delante, y el signo de la resta como dos piernas caminando hacia atrás
http://culturacientifica.com/2016/01/27/el-origen-de-los-signos-matematicos/
http://mimosa.pntic.mec.es/jgomez53/matema/conocer/simbolos.htm El origen de las fracciones, o quebrados, es muy remoto. Ya eran conocidas por los babilonios, egipcios y griegos. Los egipcios resolvían problemas de la vida diaria mediante operaciones con fracciones. Entre ellas la distribución del pan, el sistema de construcción de pirámides y las medidas utilizadas para estudiar la tierra. Esto lo comprobamos en numerosas inscripciones antiguas como el Papiro de Ahmes.
Notación
[editar]Los antiguos egipcios calculaban utilizando fracciones unitarias, como ; ; ; ; ...
El jeroglífico para una boca abierta (R) denotaba la barra de fracción (/), y un jeroglífico numérico escrito debajo de la "boca abierta", denotaba el denominador de la fracción.
|
|
Cualquier fracción que escribimos con un numerador no unitario, los egipcios la escribían como suma de fracciones unitarias distintas. De ahí que las sumas de fracciones unitarias se conozcan como "fracciones egipcias".
Los babilonios utilizaban fracciones cuyo denominador era una potencia de 60.
El sistema chino de numeración con varillas permitía la representación de fracciones. Los griegos y romanos usaron también las fracciones unitarias, cuya utilización persistió hasta la época medieval. Diofanto de Alejandría (siglo IV) escribía y utilizaba fracciones.
En el siglo VI después de Cristo fueron los hindúes quienes establecieron las reglas de las operaciones con fracciones en el siglo IV después de Cristo. En esa época, Aryabhata se preocupó de estas leyes, y después lo hizo Bramagupta, en el siglo VII.
Las reglas que utilizamos en la actualidad para trabajar con fracciones, fueron obra de Mahavira-en el siglo IX- y Bháskara-en el sigloXII.
El nombre de fracción se lo debemos a Juan de Luna, que tradujo al latín, en el siglo XII, el libro de aritmética de "Al-Juarizmi". El empleó la palabra "FRACTIO" para traducir la palabra árabe "al-Kasr", que significa QUEBRAR, ROMPER.
Las fracciones se conocen también con el nombre de "QUEBRADOS".El origen de las fracciones apunta a la necesidad de contar de medir y de repartir, entre otras.
Las fracciones unitarias egipcias (Papiro Ahmes/Rhind)
[editar]En este papiro adquirido por Henry Rhind en 1858 cuyo contenido data del 2000 al 1800 a. C. además del sistema de numeración antes descrito nos encontramos con su tratamiento de las fracciones. No consideran las fracciones en general, solo las fracciones unitarias (inversas de los naturales 1/20) que se representan con un signo oval encima del número, la fracción 2/3 que se representa con un signo especial y en algunos casos fracciones del tipo . Hay tablas de descomposición de desde n=1 hasta n=101, como por ejemplo ó , no sabemos por qué no utilizaban pero parece que trataban de utilizar fracciones unitarias menores que .
Al ser un sistema sumativo la notación es: 1+1/2+1/4 . La operación fundamental es la suma y nuestras multiplicaciones y divisiones se hacían por "duplicaciones" y "mediaciones", por ejemplo 69x19=69x(16+2+1), donde 16 representa 4 duplicaciones y 2 una duplicación.
https://sites.google.com/site/cienciasnaturaleslbjb/home Los signos × y · (multiplicación). Algunos antecedentes de estos símbolos para la multiplicación, como comenta Florian Cajori en su libro, son los siguientes. Los babilonios utilizaban de nuevo un ideograma, llamado “a-du”, para expresar la multiplicación. Diofanto no utilizaba ningún signo. En el Bakhshiili manuscript, el manuscrito más antiguo de las matemáticas de la India, simplemente se pone un factor al lado del otro. El matemático indio Bhaskara Acharia (1114-1185) utilizaba la palabra “bhavita” (o su abreviación “bha”) después de los factores.
Algunos matemáticos, como el matemático alemán Michael Stiefel (1487-1567) en su Deutsche Arithmetica (1545), el matemático flamenco Simon Stevin (1548-1620) o el filósofo y matemático René Descartes (1596-1650) en su Géométrie (1637), utilizan la letra M para la multiplicación y la letra D para la división. Por ejemplo, Stevin o Stiefel escriben la expresión 3①Msec①Mter②, donde sec expresa que es la segunda variable, la incógnita o cantidad desconocida, que aparece y ter la tercera, el círculo con el número expresa la potencia de esa variable, y las letras M y D son la multiplicación y la división, para lo que nosotros denotamos como 3 x y z2. O escriben 5②Dsec①Mter② para nuestra 5 x2 z2 / y.
Por otra parte, el matemático francés Francois Vieta (1540-1603) para expresar el producto de a y b escribía la expresión “a en b”.
La cruz de San Andrés × se utiliza por primera vez como símbolo para la multiplicación en la obra Clavis Mathematicae (1631), del matemático inglés William Oughtred (1574-1660). Aunque se utiliza también en un apéndice anónimo de la traducción de Edward Wright, de 1618, de la obra Descriptio (1614) del matemático escocés John Napier (1550-1617), aunque en este caso en forma de letra x, pero además, este apéndice parece ser que lo escribió el propio Oughtred.
Dos trozos del libro Clavis Mathematicae (1631), en el que William Oughtred introduce el signo × para la multiplicación Dos trozos del libro “Clavis Mathematicae” (1631), en el que William Oughtred introduce el signo × para la multiplicación
Mientras que Oughtred utilizaba una cruz pequeña, una cruz de San Andrés, el matemático francés Adrien-Marie Legendre (1752-1833), en su Elements de Gèomètrie (1794), utilizaba una cruz grande. El signo ×, para la multiplicación, ha llegado hasta nuestros días, en los que sigue utilizándose, aunque no ha acabado de cuajar del todo, existiendo otro signo que también es utilizado, el punto, fundamentalmente en las matemáticas.
Mientras que en Gran Bretaña tuvo una gran aceptación el signo ×, otros matemáticos, como el matemático alemán Gottfried W. Leibniz (1646-1716), creador junto con el matemático inglés Isaac Newton (1643-1727) del cálculo, no se sentían a gusto con este símbolo. En una de sus cartas al también matemático Johann Bernoulli (1667-1748), de Basilea (Suiza), escribe “No me gusta el símbolo × como un símbolo para la multiplicación, ya que se puede confundir con x;… a menudo yo simplemente relaciono dos cantidades con un punto e indico la multiplicación con RS·PQ”.
Aunque podemos decir que fue Leibniz quien introdujo el punto para la multiplicación, ya había aparecido antes. Por ejemplo, Thomas Harriot en su Artis analyticae praxis (1631) usa el punto en la expresión “aaa – 3 · bba = +2 · ccc”. El punto se adoptaría finalmente como símbolo de la multiplicación en matemáticas a lo largo del siglo XVIII.
Página manuscrita de Leibniz que contiene desarrollos en serie de la raíz de dos Página manuscrita de Leibniz que contiene desarrollos en serie de la raíz de dos
Existieron otros símbolos para el producto, así por ejemplo el matemático suizo Johann Rahn (1622-1676) utilizó el asterisco * en su obra Teutsche Algebra (1659) o Leibniz utilizó inicialmente un C tumbada, con la parte abierta hacia abajo, en su Dissertatio de arte combinatoria (1666).
Página del libro Teutsche Algebra (1659), de John Rahn, que contiene la regla del signo en la multiplicación Página del libro “Teutsche Algebra” (1659), de John Rahn, que contiene la regla del signo en la multiplicación
Muchos algoritmos para obtener productos y proporciones hacían uso, en los viejos tiempos de la aritmética, de la cruz de San Andrés (el aspa). Quizá por ello Oughtred, allá por 1631, la eligió como símbolo para sus multiplicaciones y pronto otros autores siguieron su ejemplo. Pero no todos: Leibniz, en 1698, le escribió a Johann Bernoulli: "no me gusta como símbolo para la mutiplicación, pues se confunde demasiado fácilmente con la x; ... a menudo relaciono dos cantidades con un punto interpuesto, e indico la multiplicación mediante ZC·LM". Es decir, que Leibniz, para evitar confusiones, señalaba de la misma manera proporciones y productos, con un sencillo punto.
Otra posibilidad (*) para indicar el producto es no poner nada en absoluto entre los factores, como cuando escribimos xy para indicar 'x por y'. Descartes, cuando en la página 7 de su Geometria fija la notación que va a utilizar, dice: "Et ab, pour les multiplier l'une par l'autre". Lo que no sé es si fue el primero en utilizar esta notación. La barra horizontal de las fracciones (de origen árabe) ya era usada por Fibonacci en el siglo XIII, aunque no se generalizó hasta el siglo XVI. Es, desde luego, la forma más satisfactoria, pues no solo indica la operación sino que en el caso de que sean varias las operaciones a realizar establece el orden de prioridad entre ellas (digamos que además de signo es paréntesis). La barra oblicua /, variante de la anterior para escribir en una sola línea, fue introducida por De Morgan en 1845.
En 1659 el suizo Johann Heinrich Rahn inventó para la división el signo ¸, que resulta bastante gráfico una vez que la barra de fracción es norma general. No tuvo mucho éxito en su país, Suiza, ni en la Europa continental, pero sí en Gran Bretaña y los Estados Unidos.
Los dos puntos se deben a Leibniz (1684), que los aconsejaba para aquellos casos en los que se quisiese escribir la división en una sola línea y la notación con raya de fracción no fuese por tanto adecuada. Este signo mantiene el parentesco de la división con la multiplicación, para la que Leibniz usaba un punto.
En cuanto al gnomon o ángulo que utilizamos para separar dividendo, divisor y cociente en la división larga no se dispone de una información precisa. Boyer, en su Historia de la matemática, p.282, dice: "Los árabes, y a través de ellos más tarde los europeos, adoptaron la mayor parte de sus artificios aritméticos de los hindúes, y por tanto es muy probable que también provenga de la India el método de "división larga" conocido como el "método de la galera", por su semejanza con un barco con las velas desplegadas." Pues bien: en dicho "método de la galera" se utilizaba un ángulo parecido al que se usa en la actualidad para separar el divisor de los otros números. Este símbolo ha sido usado desde el final del siglo 15 en computar el interés, ganancia, perdida e impuestos. Sin embargo, la idea tiene su origen mucho antes. Cuando el emperador romano Augustus impuso un impuesto en todos los bienes que se vendían en una subasta, centesima rerum venalium, el impuesto era de \frac{1}{100}. Otros impuesto romanos eran \frac{1}{20} sobre cada esclavo liberado y \frac{1}{25} en cada esclavo vendido. Sin reconocer esto como porcentaje, usaban fracciones reducidas a las centenas para su calculo fácil.
En la edad media, a medida que se empezo a usar grandes denominaciones de dinero, el 100 se convierto en una base comúnmente utilizada. Manuscritos italianos del siglo 15 contenían expresiones como "20 p 100" y "10 p cento" para indicar 20 por ciento y 10 por ciento. Cuando la aritmética comercial apareció al final del sigo 15, el uso del porcentaje estaba ya bien establecido. Por ejemplo, Ergio Chirinola (1481) uso "xx. per .c." par a el 20 por ciento y "viii in x percento" para 8 a 10 por ciento.
El símbolo de porcentaje, \%, seguramente evoluciono de un símbolo introducido en un manuscrito anónimo de 1425. En lugar de "P cento", que era común en ese tiempo, el autor uso el símbolo que se muestra a la izquierda.
ara 1650, el simbolo se cambio a la forma que se enseña a la izquierda. Finalmente, el "per" se dejo de usar, dejando este símbolo sin la p y se transformo en \%.
-
Símbolo en el siglo XV
-
Símbolo en el siglo XVII
-
Símbolo desde el siglo XVIII
Lee mas en : Historia de los símbolos matemáticos, por WikiMatematica.org
wikimatematica.org
Follow us: @wikimatematica on Twitter | wikimatematica on Facebook
F. Cajori, A history of mathematical notations, Dover, 1992
Arquímedes, el padre de la notación científica. El primer intento de representar números demasiado grandes fue emprendido por el matemático y filósofo griego Arquímedes, descrito en su obra El contador de Arena en el siglo III a. C. Ideó un sistema de representación numérica para estimar cuántos granos de arena existían en el universo. El número estimado por él era de 1063 granos.
Nótese la coincidencia del exponente con el número de casilleros del ajedrez sabiendo que para valores positivos, el exponente es n-1 donde n es el número de dígitos, siendo la última casilla la Nº 64 el exponente sería 63 (hay un antiguo cuento del tablero de ajedrez en que al último casillero le corresponde -2 elevado a la 63- granos). A través de la notación científica fue concebido el modelo de representación de los números reales mediante coma flotante. Esa idea fue propuesta por Leonardo Torres Quevedo (1914), Konrad Zuse (1936) y George Robert Stibitz (1939).
Aunque no es 100 por ciento seguro, parece que la idea de elevar al cuadrado o al cubo se remonta hasta el tiempo de los babilónicos. Babilonia era parte de Mesopotamia en la zona que ahora consideramos como Irak. La primera mención conocida de Babilonia se encuentra en una roca que data del siglo XXIII a.C. Y lo cierto es que aún así ellos estaban lidiando con el concepto de los exponentes, a pesar de que su sistema de numeración (el sumerio, que ahora es una lengua muerta) utilizaba símbolos para descomponer fórmulas matemáticas. Curiosamente, no sabían qué hacer con el número 0, de modo que lo delineaban como un espacio entre los símbolos.
La palabra en sí misma proviene del latín "expo", que significa "fuera de", y "ponere", que significa "celular". Si bien la palabra exponente pasó a significar cosas diferentes, el primer uso moderno registrado de exponente en matemáticas fue en un libro llamado "Integra Arithemetica", escrito en 1544 por el autor inglés y matemático Michael Stifel. Pero él simplemente estaba trabajando con una base de dos, de modo que, por ejemplo, el exponente 3 significaba que la cantidad de números 2 que tendrías que multiplicar para obtener 8. Lo que se vería así: 2 ³ = 8. El método de Stifel se diría que es un poco retrógrado en comparación con la forma en que pensamos acerca del tema hoy. Él diría que "el 3 es la configuración del 8". Pero hoy en día, nos referimos a eso simplemente como una ecuación de 2 al cubo. Hay que recordar que él estaba trabajando exclusivamente con una base o un factor de 2 y traduciendo del latín un poco más literalmente de lo que hacemos actualmente. Las raíces cuadradas son expresiones matemáticas que surgieron al plantear diversos problemas geométricos como la longitud de la diagonal de un cuadrado.
El Papiro de Ahmes datado hacia 1650 a. C., que copia textos más antiguos, muestra cómo los egipcios extraían raíces cuadradas.
En la antigua India, el uso del cuadrado y la raíz cuadrada fue al menos tan antiguo como los Sulba Sutras, fechados entre el 500 y el 300 a. C. Un método para encontrar muy buenas aproximaciones a las raíces cuadradas de 2 y 3 es dado en el Baudhaiana-sulba-sutra.
Ariabhatta (476-550) en su tratado Ariabhatíia (sección 2.4), dio un método para encontrar la raíz cuadrada de números con varios dígitos.
Los babilonios también usaron las raíces cuadradas para hacer cálculos repitiendo las mismas divisiones una y otra vez. Las raíces cuadradas fueron uno de los primeros desarrollos de las matemáticas, siendo particularmente investigadas durante el periodo pitagórico, cuando el descubrimiento de que la raíz cuadrada de 2 era irracional (no se podía medir) o no expresable como cociente alguno, lo que supuso un hito en la matemática de la época. Posteriormente se fue ampliando la definición de raíz cuadrada.
Inicialmente mostraron su utilidad para la resolución de problemas trigonométricos y geométricos, como la diagonal de un cuadrado o el teorema de Pitágoras. Posteriormente fueron ganando utilidad para operar con polinomios y resolver ecuaciones de segundo grado o superior, siendo una de las herramientas matemáticas más elementales hoy en día. El símbolo de la raíz cuadrada fue introducido en 1525 por el matemático Christoph Rudolff.
El signo no es más que una forma estilizada de la letra r minúscula para hacerla más elegante, alargándola con un trazo horizontal, hasta adoptar el aspecto actual, que representa la palabra latina radix, que significa raíz. También se cree que puede haber surgido de la evolución del punto que a veces se usaba anteriormente para representarlo. John Napier estudió acerca de ellos entre 1590 y 1617. La primera obra que publicó en ese sentido fue Mirifici Logarithmorum Canonis Descriptio (Descripción de una admirable tabla de logaritmos) en 1614. Allí describe cómo utilizar los logaritmos para resolver problemas con triángulos y da una tabla de logaritmos. En 1619 su hijo Robert publica póstumamente Mirifici logarithmorum canonis constructio (Construcción de una admirable tabla de logaritmos), donde se explica cómo se construye la tabla de logaritmos.
Si bien en el comienzo denominó «números artificiales» a los logaritmos, él mismo crearía luego el nombre con el que se los conoce actualmente, al combinar las palabras griegas «logos» (proporción) y «arithmos» (número).
Transmisión del sistema indo-arábigo a Occidente
[editar]Varios autores del siglo XIII contribuyeron a esta difusión, destacamos a: Alexandre de Villedieu (1225), Sacrobosco (circa 1195, o 1200-1256) y sobre todo Leonardo de Pisa (1180-1250). Este último, conocido como Fibonacci, viajó por Oriente y aprendió de los árabes el sistema posicional hindú. Escribió un libro, El Liber abaci, que trata en el capítulo I la numeración posicional, en los cuatro siguientes las operaciones elementales, en los capítulos VI y VII las fracciones: comunes, sexagesimales y unitarias (¡no usa los decimales, principal ventaja del sistema!), y en el capítulo XIV los radicales cuadrados y cúbicos. También contiene el problema de los conejos que da la serie: con .
No aparecen los números negativos, que tampoco consideraron los árabes, debido a la identificación de número con magnitud (¡obstáculo que duraría siglos!). A pesar de la ventaja de sus algoritmos de cálculo, se desataría por diversas causas una lucha encarnizada entre abacistas y algoristas, hasta el triunfo final de estos últimos.
Numeración Hindu
[editar]Numeración Arábiga
[editar]MATEMÁTICAS DE LA PREHISTORIA
¿En qué momento? Comenzó la humanidad a pensar en términos de relaciones numéricas y geométricas & La tradición pretende que la ciencia matemática empezó en Grecia// hacia el siglo 5 a 100 para no dejar a las civilizaciones anteriores más que parcelas cuyo contenido matemático es a la vez deslavazado y concreto: Si el origen del hombre sigue siendo todavía enigmático desde distintos puntos de vista- es sin embargo casi seguro que, hacia el año 400 000 a.C. (hombre de Neandertal), el hombre comenzó a pensar. Desde este momento, el hombre de la prehistoria adquiere conciencia del medio en el que vive y tiene que procurar, con toda urgencia, su supervivencia.
Las numerosas excavaciones arqueológicas realizadas en depósitos y sedimentos neolíticos revelan ya la existencia de una industria perfeccionada y actividades sociales propias de una sociedad en marcha. Dos elementos matemáticos importantes surgen en esta sociedad prehistórica: 1) un lenguaje articulado en el que hay un sistema de números; 2) utensilios y construcciones en los que intervienen relaciones espaciales. Existen algunos factores que pueden persuadirnos de que el hombre primitivo poseía una cierta idea del concepto de número. • Por ejemplo, numerosas tribus primitivas que viven actualmente en Australia y Polinesia poseen un sistema de números, más o menos elaborado. Estas tribus, que viven en la edad de piedra (varias de ellas no poseen ni agricultura, ni utensilios perfeccionados como el arco y la flecha), consiguen contar y utilizar un lenguaje de tipo descriptivo. • Se conoce el descubrimiento, en Checoslovaquia, de un hueso perteneciente a un lobo joven, hueso sobre el que aparece una sucesión de cincuenta y cinco incisiones, dispuestas en dos series, por grupos de cinco. Este hueso fue descubierto en sedimentos que datan de hace aproximadamente 30 000 años.
FORMACIÓN DEL NÚMERO EN EL HOMBRE PRIMITIVO
Antes de que existiese un lenguaje capaz de favorecer la comunicación verbal, el hombre primitivo podía observar en la naturaleza fenómenos cuantitativos: un árbol y un bosque, una piedra y un montón de piedras, un lobo y una manada de lobos, etc. Esta distinción entre la unidad y la pluralidad, la estableció, sin duda, muy pronto. Igualmente, la noción de par —dos pies, dos manos, dos ojos, etc.— debió llamar su atención. A partir de estas rudimentarias observaciones, el hombre primitivo extrae gradualmente la idea de comparación y asocia, a cada objeto observado, un signo, una cosa que le sea familiar. Puede así asociar a una colección de objetos observados un grupo de signos o de cosas. Esta colección de signos puede ser muy variada según las tribus o pueblos primitivos: una tribu (o incluso un individuo) utilizará rayas hechas en la madera, en un hueso o en la arena; otra recurrirá a un montón de guijarros o incluso a cocos; y otra preferirá los gestos de la mano (posiciones de la mano sobre una parte del cuerpo) o de la cabeza; etc. La enumeración de un grupo de objetos observados deja paso a la numeración con la aparición de para un lenguaje articulado .//escrito o hablado+. Esta transición corresponde probablemente al cambio de vida del hombre primitivo que se convierte en productor, comerciante, en vez de simple proveedor de alimento. El comerciante necesita un lenguaje articulado para conseguir vender sus productos y debe poseer un sistema de números para contar. El productor evalúa la cantidad de objetos producidos, el número de corderos criados, las pérdidas por robo, y todo esto presupone el conocimiento de un sistema de numeración adecuado al tipo de vida del hombre primitivo. La numeración presenta también variantes según las tribus: Por ejemplo, los antiguos sumerios utilizaban las palabras «hombre», «mujer» y «varios», en lugar de «uno», «dos» y «tres», respectivamente. Así el hombre simboliza el número 1. Por matrimonio, él y su mujer representaban el número dos. Todo lo que sobrepasase numéricamente el dos estaba simbolizado por «varios». Los pigmeos de Africa utilizan el sistema repetitivo siguiente: a, oa, ua, oa-oa, para los números uno, dos, tres y cuatro, respectivamente. Las tribus kamilarai de Australia utilizan también un sistema repetitivo: uno se dice «mal»; dos se dice «bulan»; tres es «guliba»; cuatro corresponde a «bulan bulan»; etc. No obstante, la sustitución de los objetos por palabras del lenguaje no significa aún que el concepto de número esté en el pensamiento del que enumera. En esta fase, el hombre primitivo, que asocia a tres vacas tres palabras distintas, no puede, sin las palabras, pensar en el número tres. Además, experiencias etnográficas efectuadas con tribus primitivas han demostrado que el conocimiento de una sucesión ordenada de palabras numéricas no lleva necesariamente consigo la comprensión del concepto de número cardinal. Eliminar el soporte material del objeto observado, para no retener más que el elemento numérico al que corresponde en el proceso de numeración, equivale de hecho a exigir que el observador sea capaz de abstraer. Esta etapa decisiva no se adquiere sino progresivamente y en la medida en que se distinguen dos conceptos importantes: el número cardinal, que proporciona la expresión cuantitativa, y el número ordinal, que pone de manifiesto la existencia de un primer elemento seguido de un segundo y de un tercero, etc. El hombre primitivo piensa en un número cuando capta bien las relaciones siguientes: 1) la naturaleza de los objetos que se van a contar no desempeña ningún papel en la numeración; 2) el orden en el que los elementos son observados no influye en el resultado final, es decir, en el número cardinal; 3) el último elemento contado corresponde de hecho, en la medida en que sólo sea necesario el resultado de la cuenta, al número cardinal de la colección. Por consiguiente, el paso difícil de dar consiste en reconocer al último elemento contado como aquel que expresa «cuántos elementos contiene el conjunto que se quiere contar». ¿A qué nivel las tribus de hombres prehistóricos cumplieron las condiciones antes citadas? Esta pregunta permanecerá probablemente sin respuesta debido a la ausencia casi total de documentos relativos a este tipo de cuestiones.
AGRUPAMIENTO DE LOS NÚMEROS
Si los signos para representar los números precedieron cronológicamente a las palabras, el agrupamiento de los signos (rayas verticales, guijarros, dedos de la mano, etc.) influenció sin duda, de manera directa, la base del sistema de numeración elegido. Parece que las tribus más primitivas utilizaron primero el agrupamiento de dos en dos, después de cuatro en cuatro y de seis en seis. Ocasionalmente, las variantes corresponden a agrupamientos de tres en tres (tribus americanas). Un sistema muy natural y en boga corresponde a los dedos de la mano y puede así implicar agrupamientos de cinco en cinco (dedos), de diez en diez (dedos) y de veinte en veinte (dedos de los pies y de las manos). En un principio, este sistema presenta la ventaja, no solamente de preferir agrupamientos naturales y fácilmente accesibles, sino también de favorecer, por la «disposición» de los dedos, una distinción entre número cardinal y número ordinal. Estos agrupamientos de cinco, diez y veinte objetos aparecen en varias partes del mundo. Otros agrupamientos fueron también utilizados por ciertas tribus primitivas, especialmente los agrupamientos de doce, de sesenta y de ocho. Documentación sobre una investigación emprendida por la Universidad de Stanford sobre 307 sistemas de numeración que se encuentran en las tribus primitivas americanas. Aporta que, de estos sistemas, 146 pertenecen a los agrupamientos de diez, 106 a los agrupamientos de cinco y diez, 81 son binarios, 35 sop de base veinte y de base cinco y veinte, 15 pertenecen a los agrupamientos de cuatro, 3 son agrupamientos de tres y uno solo corresponde a la base ocho. Una vez comprendida perfectamente la noción de agrupamiento, es natural que el hombre primitivo asigne entonces un símbolo particular al agrupamiento utilizado. Está ahora en posesión de los elementos que podrá combinar para inventar su sistema de numeración.
SISTEMAS DE NUMERACIÓN
La necesidad de un sistema de numeración proviene de la naturaleza de las actividades propias de un pueblo primitivo. Las tribus que poseían grandes rebaños domesticados o que practicaban una agricultura diversificada y desarrollada sintieron muy pronto la necesidad de elaborar un sistema que les permitiese utilizar números grandes y favoreciese la invención de un calendario. ¿Cuáles son los procedimientos utilizados durante la prehistoria (o que tienen en ella su origen) y que dieron lugar a los diferentes sistemas de numeración? Un primer procedimiento consiste en prolongar el agrupamiento añadiendo unidad a unidad. Por ejemplo, si el hombre primitivo utiliza los cinco dedos de su mano izquierda como agrupamiento, utilizará los dedos (uno a uno) de su mano derecha para prolongar la cuenta hasta diez. Otra posible extensión consistiría en utilizar los dedos de los pies. Este procedimiento, aunque muy simple, introduce dificultades enormes en el lenguaje, puesto que requiere la creación de nuevas palabras. Otro procedimiento, mucho más eficaz, consiste en utilizar el principio de la «repetición» en la numeración de los objetos contados. Por ejemplo, en base tres, los pigmeos de Africa emplean el sistema repetitivo siguiente: 1, 2, 3, 4, 5 y 6 se corresponden con a, oa, ua, oa-oa, oa-ua y ua-ua. Al hombre primitivo, que utiliza una mano-de cinco dedos como base, le es suficiente añadir la otra mano para contar hasta diez; después, una segunda persona registra las cuentas de diez a veinte,y así sucesivamente. Una variante consiste en utilizar los diez dedos como base y proceder así de la misma forma que antes. Este procedimiento está catalogado como «sistema aditivo no posicional»; su principal defecto es que utiliza un gran número de símbolos. El tercer método, muy poco empleado durante la prehistoria, se basa esencialmente en el principio de la posición. Cualquier símbolo posee el valor indicado por la posición que ocupa en la sucesión de símbolos que representa un número u otro. El ejemplo por excelencia de este tipo de sistema, llamado «sistema posicional», es nuestro sistema decimal. El desarrollo de los sistemas de numeración de la época prehistórica no fue, probablemente, más allá del tipo aditivo no posicional. No obstante, esto no impidió a los hombres primitivos establecer los primeros elementos de una aritmética práctica y de una geometría orientada a la medición de áreas y volúmenes. Con la aparición del comercio, la industria y la agricultura, el hombre primitivo debe no solamente saber contar, sino también ser capaz de hacer un balance de sus actividades comerciales. Los métodos primitivos varían enormemente cuando se trata de registrar las diversas formas de actividad económica: marcas en la madera, nudos en una cuerda, grupos de guijarros o de cocos, rayas en papiros o en tablillas de arcilla, etc. Y hacer el balance implicaba necesariamente conocer las reglas elementales de cálculo numérico. No era cuestión en aquella época de utilizar números que no fuesen los naturales. Los números enteros, racionales, irracionales, complejos. por no citar más que éstos, son invenciones de nuestra era . GEOMETRÍA EMPÍRICA.
La adquisición de los rudimentos del cálculo aritmético da lugar a la medición de longitudes, áreas y volúmenes. Las unidades de medición se eligen con frecuencia entre las partes del cuerpo humano: el dedo, el pie, el pulgar, la mano, el antebrazo. Los volúmenes se miden con ayuda de cestos o de conchas de tamaño «standard». La construcción de las casas se lleva a cabo con ayuda de reglas que garantizan la existencia de líneas y ángulos rectos. La geometría que se utiliza es empírica y está esencialmente dirigida a un fin utilitario o ritual. La justificación de las reglas utilizadas y de las convenciones elegidas es inexistente, por lo menos en los documentos recogidos sobre esta época. La geometría aparece también en las pinturas y motivos dibujados por estos pueblos primitivos. Una gran riqueza de figuras geométricas se encuentra en vasos, cestos, muros de cavernas. Son abundantes los ejemplos de semejanza y de distintas formas de simetría en las decoraciones del Neolítico. La imaginación geométrica de estos pueblos es de una riqueza difícil de sospechar. Hay que mencionar también que el desarrollo de las matemáticas estuvo en esta época muy influenciado por la astronomía. Los pueblos primitivos poseían ciertos conocimientos relativos al sol, la luna y las estrellas. Además, un pueblo agrícola debía llevar la cuenta de los días y de las noches, así como de las distintas estaciones. Los pueblos primitivos adoptan casi todos un calendario lunar con el fin de diferenciar los aspectos cambiantes de la vegetación y poseer unidades de tiempo útiles y convenientes. Por último, es indispensable subrayar la influencia de la religión sobre la vida primitiva, tanto en el plano espiritual como en el de las acciones diarias del hombre primitivo. Incluso si la civilización se estableció sobre un soporte religioso inherente a prácticas rituales, se debe, no obstante, considerar cuál fue el papel de la práctica religiosa del hombre primitivo en su concepción del número. Es muy probable que el desarrollo de las matemáticas pudiese haber estado influenciado, en sus orígenes, por las prácticas religiosas; en particular, el concepto de número y la geometría del hombre primitivo reflejan aspectos ligados al ámbito religioso.
RESUMEN
Las civilizaciones de la época neolítica o prehistórica, caracterizadas por la caza y una agricultura y un comercio rudimentarios, manifestaron interés por el número y la geometría empírica. Este comienzo de las matemáticas fue originado por las necesidades de su vida social y económica, y estuvo influenciado también por la religión y la magia.
Los hombres primitivos desarrollaron sistemas de numeración (de tipo aditivo no posicional) que les permitían efectuar cálculos elementales con números naturales (adición, sustracción, multiplicación). La geometría empírica del hombre primitivo se reduce a algunas reglas para medir longitudes y volúmenes. Los dibujos de rico colorido contienen figuras geométricas en las que predomina la simetría. La mayoría de los pueblos primitivos inventaron un calendario lunar.
Fuentes
[editar]Adaptado de http://iesllerena.juntaextremadura.net/descargas/hojamatematica01dic2009.pdf Las matemáticas en el Antiguo Egipto constituyeron la rama de la ciencia que más se desarrolló, y podemos estudiarlas a partir del papiro Rhind, que enuncia: Reglas para estudiar la naturaleza y para comprender todo lo que existe, todo misterio, todo secreto.
Previamente
[editar]La introducción de un calendario, basado en la división del año en doce meses de treinta días y el agregado de cinco días festivos, el erigimiento de edificios monumentales perfectamente realizados, como las pirámides, sugieren , conjuntamente a una técnica avanzada, una buena apoyatura matemática. Los conocimientos actuales respecto a lo anterior están restringidos a pocas listas de ejemplos, de muestra para encumbrados funcionarios; entre los más importantes, se puede mencionar: Papiro de Moscú, Rollo de Cuero, Papiro de Rhind, redactado por Ahmés.[3]
Métodos
[editar]El punto de vista tradicional sobre el Imperio Antiguo nos dice que los egipcios dedicaron la aritmética para usos prácticos, con muchos problemas del tipo: Cómo un número de panes se pueden dividir en partes iguales entre un número de personas. Los problemas de los papiros de Moscú y Rhind se expresan en un contexto educativo, y los traductores han encontrado tres definiciones abstractas del número y otras formas más complejas de aritmética. Las tres definiciones abstractas están en la tablilla de madera de Ajmin, el EMLR y el papiro matemático de Rhind. Las formas más complejas de aritmética incluyen el uso de tablas de fracciones, así como restos de la sustracción no aditiva y de la división. Los restos son precedidos por series binarias y seguidos por un factor de posicionamiento en la tablilla de Ajmin, el PMR y otros textos.
Para la adición y la multiplicación, emplearon el método de duplicar, y de dividir por dos, un número conocido para encontrar la solución. Para la sustracción y la división emplearon otros métodos que todavía no se conocen en su totalidad. El «método de posición falsa» puede no haber sido utilizado para la división y los problemas simples del álgebra.
En el Imperio Antiguo, usaban un sistema numérico de base 10, en el Imperio Nuevo, fracciones unitarias y tablas de segundos resultados; los escribas solucionaron varios problemas matemáticos muy complejos, 84 de los cuales se explican en el papiro matemático de Rhind.
Según Heródoto, los egipcios son los padres de la Geometría, pero gracias a sus monumentos y sus papiros también sabemos hoy que disponían de un sistema de numeración adicional que les permitía trabajar con fracciones de una forma muy especial ya que el numerador siempre era la unidad.
Descripción
[editar]Alrededor del año 2700 a. C., los egipcios introdujeron el primer sistema de numeración completamente desarrollado de base 10. Aunque no era un sistema posicional, permitió el uso de grandes números y también de fracciones en la forma de fracciones unitarias: fracciones del Ojo de Horus, y varias fracciones binarias.
En esa misma época, las técnicas egipcias de construcción incluyeron sistemas de topografía, marcando el norte por la situación del sol al mediodía. Antes del año 2000 a. C., comenzaron a aparecer referencias claras que citaban aproximaciones para π y raíces cuadradas. Las relaciones del número exacto, tablas aritméticas, los problemas del álgebra y aplicaciones prácticas con pesos y medidas también comenzaron a aparecer alrededor de 2000 a. C., con varios problemas solucionados por métodos aritméticos abstractos.
Fuentes
[editar]Nuestro conocimiento de las matemáticas egipcias ha sido incompleto por la falta de fuentes disponibles. La más famosa es el papiro Rhind, o Ahmes, el papiro matemático (PMR), un texto que puede ser leído comparando muchos de sus elementos con otros textos como el EMLR y las tablillas de madera de Ajmim. El PMR se fecha a partir del Segundo periodo intermedio de Egipto (circa 1650 a. C.), pero el autor lo identifica como copia de un papiro del Imperio Medio. El papiro matemático de Rhind contiene una tabla de la serie egipcia de la fracción 2/n (101 entradas) y 84 problemas. Utiliza una forma de aritmética que usa fracciones unitarias, que eran precedidas a menudo por un número entero. Tomando las fracciones de los números enteros y de la unidad juntas como una declaración, como cocientes y restos, o simplemente como aritmética del resto.
El PMR también incluye fórmulas y métodos para cálculo de áreas, y operaciones aritméticas para la adición, la substracción, la multiplicación y la división de las fracciones unitarias. Contiene evidencia de otros conocimientos matemáticos, incluyendo números compuestos y primos; medias aritméticas, geométricas y armónicas; y un método simple de la tabla de Eratóstenes y del número perfecto. También muestra cómo solucionar ecuaciones lineales de primer orden así como sumar series aritméticas y geométricas.
Los papiros de Berlín, escritos alrededor del año 1300 a. C., muestran que los antiguos egipcios habían solucionado dos ecuaciones de segundo grado, Diofánticas, aunque el método de Berlín para solucionar x² + y² = 100 no se ha confirmado en un segundo texto.
Otras fuentes son el papiro matemático de Moscú (PMM), el papiro de Reisner, la tablilla de madera de Ajmim (Museo de El Cairo) (AWT), y varios otros textos que incluyen prescripciones médicas.
Números
[editar]En el antiguo Egipto, fueron utilizados dos tipos de numeración. Uno, escrito en jeroglíficos, era un sistema decimal, con signos distintos para 10, 100, 1000, etc., que se usó en el periodo Predinástico. El segundo, el sistema hierático, escrito con un nuevo tipo de cifras que asimilaba un número a un símbolo, se diferenció del sistema jeroglífico por simplificar los símbolos para poder escribir más rápido, y comenzó alrededor de 2150 a. C.
Una numeración jeroglífica tardía fue modificada y adoptada en el Periodo Romano para las aplicaciones oficiales, y las fracciones egipcias en las situaciones cotidianas.
Números en hierático
[editar]Para los números hieráticos utilizaron un símbolo para cada número, sustituyendo las cifras que habían sido utilizadas para designar múltiplos de la unidad. Por ejemplo, utilizaban dos símbolos para escribir tres, treinta, trescientos, etcétera, en un sistema que reemplazó al modo jeroglífico.
Como la mayoría de textos administrativos y de contabilidad fue escrita en papiros u ostracas, y no grabados en piedra como los textos jeroglíficos, emplean el sistema hierático de escritura, siempre los casos encontrados de números escritos en hierático son posteriores al Imperio Antiguo. Los papiros de Abusir son una recopilación particularmente importante de textos que utilizan estos números.
Boyer demostró hace 50 años que esa escritura utilizaba un sistema de numeración diferente, usando símbolos individuales para los números 1 a 9, los múltiplos de 10 entre 10 y 90, las centenas a partir del 100 al 900, y los millares a partir de 1000 a 9000. Un número grande como 9999 se podía escribir con solamente cuatro signos, combinando los signos para 9000, 900, 90, y 9, opuestas a 36 jeroglíficos.
Dos papiros matemáticos famosos que usan la escritura hierática son el de Moscú y el de Rhind. Este último contiene ejemplos de cómo los egipcios hicieron sus cálculos matemáticos, y los números fueron designados poniendo una línea sobre la letra asociada al número que era escrito, como /A. Este método de escribir números se extendió por el Cercano Oriente, y los griegos, 1500 años más tarde, lo usaban en dos de sus alfabetos, jónico y dórico, para representar sus números: /alfa = 1, /beta = 2 y así sucesivamente. Respecto a las fracciones, los griegos escribieron 1/n como n', por lo que en la numeración y resolución de problemas los griegos adoptaron o modificaron la numeración egipcia, la aritmética y otros aspectos de las matemáticas egipcias.
Adición y sustracción
[editar]Simplemente unían los signos para sumar.
|
Y |
|
Si los pies señalaban en la dirección de la escritura, significaban suma, si no resta.
La sustracción está descrita en el rollo de cuero EMLR (1800 a. C.), un documento que incluye cuatro métodos de adición.
Multiplicación
[editar]La multiplicación egipcia se hacía por duplicaciones del multiplicando, y es conocido como duplicación y mediación, y se basa en la propiedad distributiva de la multiplicación.
El método utilizado solo requiere saber sumar:
Si deseamos multiplicar X por Y, siendo X mayor que Y (si no lo fuera, se procedería a invertir el orden de los factores, se trata de realizar el menor número posible de operaciones)
- En la primera columna se escribe la serie: X, 2X, 4X... (obteniendo cada cifra duplicando la precedente)
- En la segunda columna se escribe la serie: 1, 2, 4, 8...(2n < Y) (obteniendo cada cifra duplicando la precedente, hasta el último número que no supere la cifra Y)
- En la tercera columna se marcan las cifras necesarias, de la segunda columna, de tal forma que expresemos el valor de Y como la suma del menor número de sumandos. Esto se puede hacer de dos formas por adición o sustracción: Sustracción, se resta al valor de Y, o sea 14, el último valor de la columna B, que es 8, obteniendo 6. Ahora a 6 hay que restarle el mayor posible de la misma columna, en este caso 4, obteniendo 2 y se repite la operación hasta que el resultado dé 0, en este caso quedaría completado con la casilla siguiente. Adición, mentalmente se suman 8+4+2=14 y se marcan las filas pertinentes.
- El resultado es la suma de las cifras de la columna primera marcadas.
Como un corte para números más grandes, el multiplicando se puede también multiplicar inmediatamente por 10, 100, etc.
Por ejemplo, el problema 69 en el papiro de Rhind (RMP) proporciona el resultado siguiente:
| Para multiplicar 80 x 14 | |||||||||
| Números egipcios | Números actuales | ||||||||
| A | B | cifras a sumar | A | B | |||||
|
|
80 | 1 | ||||||
|
|
Plantilla:Bien | 160 | 2 | |||||
|
|
Plantilla:Bien | 320 | 4 | |||||
|
|
Plantilla:Bien | 640 | 8 | |||||
| Resultado: | |||||||||
|
160 + 320 + 640 = 1.120 | ||||||||
Nota: El signo Plantilla:Bien indica las cifras intermedias que se han de sumar para obtener el resultado final: se desecha la primera línea (A = X = 80) y se detiene la operación en B = 8, ya que la siguiente cifra (16) es mayor que Y (14).
La matemática hierática del Imperio Medio mantuvo esta forma de multiplicación jeroglífica que era un sistema lento, pero seguro: al escriba le bastaba saber duplicar las cifras para hacer sus cálculos; por eso no necesitaron crear tablas de multiplicar, como luego se hizo en Mesopotamia.
División
[editar]La división se efectuaba por el procedimiento inverso de la multiplicación: Se marcan los números de la columna B cuya suma es el dividendo, y sumando los correspondientes de la columna A se halla el cociente. Así:
| Para dividir 168 entre 8 | |||||||||||
| Números egipcios | Números actuales | ||||||||||
| A | B | cifras a sumar | A | B | |||||||
|
|
Plantilla:Bien | 1 | 8 | |||||||
|
|
2 | 16 | ||||||||
|
|
Plantilla:Bien | 4 | 32 | |||||||
|
|
8 | 64 | ||||||||
|
|
Plantilla:Bien | 16 | 128 | |||||||
| Resultado: | |||||||||||
|
1 + 4 + 16 = 21 | ||||||||||
Notas:
- Las columnas se detienen cuando la columna B llega al número anterior al dividendo.
- El signo Plantilla:Bien indica las cifras intermedias que se han de sumar para obtener el resultado final, aquellas que en la columna B suman 168: 128 + 32 + 8.
Cuando el cociente no es exacto, es necesario introducir las fracciones.
- Así, para dividir 169 entre 8 se opera igual, pero habría que añadir 1/8 pues 21 = 16 + 4 + 1 + 1 dividido por 8. Solución 21 + 1/8
- Para dividir 170 entre 8 se opera igual, pero habría que añadir 1/8 + 1/8. Solución 21 + 1/8 + 1/8 etc.
Fracciones
[editar]Fracciones en textos matemáticos
[editar]Los números racionales se podían también expresar, pero solamente como sumas de fracciones unitarias, es decir sumas de los inversos de los números enteros positivos, a excepción de 2/3 y de 3/4. El jeroglífico que indicaba una fracción era una boca, y significaba la "parte":
Las fracciones eran escritas con el signo r encima del número; en notación actual: 1 como numerador, y el número escrito debajo como denominador. Así, 1/3 se representaba como:
Había símbolos especiales para el 1/2 y para dos fracciones, 2/3 (usado con frecuencia) y 3/4 (utilizado algo menos):
Si el denominador era demasiado grande, la "boca" era puesta al principio del "denominador":
- Fracciones para medidas de capacidad

Para las medidas agrarias de superficie y capacidad, conservaron un sistema mucho más antiguo, basado en las divisiones por dos de 1/2, fracciones representadas en el Ojo de Horus (ojo izquierdo que le fue arrancado por Seth). Cada fracción se representaba por el jeroglífico correspondiente del ojo:
|
|
|
|
|
|
Por ejemplo:
Significa 1 + 1/4 + 1/8 + 1/32 (45/32 = 1'40625) heqat de cebada.
Fracciones agrarias
[editar]Utilizaban un tercer sistema de notación para medir los campos:
de setat, de setat, de setat, etc.
Por ejemplo:
Significa: 1/4 + 1/8 (3/8 = 0'375) de arada.
Repartos proporcionales
[editar]Debido al sistema económico y social, donde todo trabajador estaba a cargo del faraón o los templos, y en el cual en todo comercio o trabajo se operaba por trueque, los egipcios adquirieron una gran maestría en el manejo de fracciones.
Al escriba correspondía llevar a cabo una gran contabilidad material, tanto el registro de la producción (suministro de simientes, herramientas, materias primas y recogida de cosechas), como para el reparto de los bienes de consumo (alimentos, vestidos,) entre los miembros de las comunidades agrícolas o artesanas. Esto explica la importancia de los problemas de reparto y de la fidelidad al sistema de fracciones.
Por ejemplo, en el problema nº 4 del Papiro de Rhind:
Dividir 7 panes entre 10 hombres.
Tienes que multiplicar 2/3 + 1/30 por 10. Resultado, 7.
| 1 | + | |||
| 2 (*) | + | |||
| 4 | + + | |||
| 8 (*) | + | |||
| Total: 7 panes; está bien. | ||||
Geometría
[editar]- El volumen del tronco de pirámide se basa en la fórmula
- La ecuación numérica, anticipo del teorema de Pitágoras, , es posible invención de la matemática de los antiguos egipcios.
- Dan una aproximación para mediante , tal vez obtenida de una transformación aproximada del octante en un triángulo rectángulo isósceles. [4]
Noción de calidad
[editar]Es evidente que a los egipcios les interesaba sólo el aspecto práctico de la ciencia. Esto explica por qué, especialmente en los cálculos de repartimiento, los escribas tuvieran en cuenta, además del número de partes, la calidad de la mercancía. Este concepto se llamaba pesú, que significa literalmente valor de cocina, e indica el número de unidades que se puede obtener de una fanega: si el pesú de un pan es 12, significa que ese pan tiene 1/12 de fanega; el pesú de una jarra de cerveza (otro elemento fundamental en la alimentación) significa el número de jarras obtenidas de una fanega de grano. Cuanto más bajo sea el número del pesú, más fuerte es la cerveza, o más grande o compacto el pan.
Este elemento de cálculo es fundamental para remunerar los servicios, por lo cual interviene en numerosos problemas.
Por ejemplo:
«Tres 1/2 fanegas de harina se transforman en 80 panes. Dime cuánta harina tiene cada pan y cuál es su pesú.»
«Si te dicen: He aquí 100 panes de fuerza (pesú) 10, que hay que cambiar por panes de fuerza (pesú) 15. ¿Cuánto darás a cambio?» (Da cómo respuesta que 100 panes de 10 equivalen a 150 de 15).
Hay que observar que el valor pesú variaba en proporciones apreciables, y que los escribas a veces tenían que entregar líquidos por sólidos o viceversa.
Bibliografía
[editar]- Arnaldez, Roger y otros (1988). Las antiguas ciencias del Oriente.. Barcelona: Ediciones Orbis S.A.. ISBN 84-402-0159-1.
Enlaces externos
[editar]https://www.um.es/docencia/pherrero/mathis/egipto/egipt.htm
https://es.wikipedia.org/wiki/Matem%C3%A1ticas_en_el_Antiguo_Egipto

1 + 24/60 + 51/602 + 10/603 = 1.41421296...
La matemática babilónica (también conocida como matemática asirio-babilónica)[5][6][7][8][9][10] se refiere al conjunto de conocimientos matemáticos que desarrollaron los pueblos de Mesopotamia, desde la temprana civilización sumeria hasta la caída de Babilonia en el 539 a. C. Los textos de matemática babilónica son abundantes y están bien editados;[11] se pueden clasificar en dos períodos temporales: el referido a la Antigua Babilonia (1830-1531 a. C.) y el correspondiente al seléucida de los últimos tres o cuatro siglos a. C. En cuanto al contenido, hay apenas diferencias entre los dos grupos de textos. La matemática babilónica permaneció constante, en carácter y contenido, por aproximadamente dos milenios.[11] En contraste con las escasas fuentes de matemática egipcia, nuestro conocimiento de la matemática babilónica se deriva de unas 400 tablillas de arcilla, desenterradas desde 1850. Trazadas en escritura cuneiforme, las tablillas se grababan mientras la arcilla estaba húmeda, y luego eran endurecidas en un horno o calentándolas al sol. La mayoría de las tablillas de arcilla recuperadas datan del 1800 al 1600 a. C., y abarcan temas que incluyen fracciones, problemas de álgebra, ecuaciones cuadráticas y cúbicas y tríos de enteros en aplicación del esbozo del teorema de Pitágoras, demostrado aún en Grecia tiempo después.[12] La tablilla babilónica YBC 7289 da una aproximación de con cinco decimales de exactitud.
Numerales babilónicos
[editar]El sistema de numeración babilónico era el sistema de numeración sexagesimal (base-60). De aquí se deriva el uso moderno de 60 segundos en un minuto, 60 minutos en una hora, 360 grados en un círculo. Los babilonios fueron capaces de realizar grandes avances en matemáticas por dos razones: en primer lugar, el número 60 es un número compuesto, con muchos divisores 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 y 60, lo cual facilita los cálculos con fracciones; adicionalmente, a diferencia de egipcios y romanos, los babilonios, indios y mayas poseían un verdadero sistema de notación posicional, en donde los dígitos escritos en la columna de la izquierda representan valores mayores (tal y como en nuestro sistema de base diez: 734 = 7×100 + 3×10 + 4×1). Los sumerios y babilonios fueron pioneros a este respecto.
El sistema sexagesimal de numeración se ha establecido, posiblemente, de la fusión de otros dos antiguos: uno estrictamente decimal (semítico) de signos para monedas, pesos y medidas y otro, duodecimal. En textos astronómicos hay compulsa entre números positivos y números negativos; todas la parejas de factorización igual a 60 o de sus potencias son recogidas en tablillas. [13].
Matemática sumeria (3000 a 2300 a. C.)
[editar]Los antiguos sumerios de Mesopotamia desarrollaron un complejo sistema de metrología desde el año 3000 a. C. A partir del año 2600 a. C. en adelante, los sumerios escribieron tablas de multiplicar en tablillas de arcilla y realizaron ejercicios geométricos y problemas de división. Las trazas más antiguas de los numerales babilónicos se remontan también a este período.[14]
Matemática en la Antigua Babilonia (2000-1600 a. C.)
[editar]El período de la Antigua Babilonia es el período al cual pertenecen la mayoría de las tablillas de arcilla, que es por lo que la matemática de Mesopotamia es comúnmente conocida como matemática babilónica. Algunas tablillas de arcilla contienen listas y tablas, otras contienen problemas y soluciones desarrolladas.
Diversas ramas y otros temas
[editar]Aritmética
[editar]Los babilonios hicieron uso extensivo de tablas precalculadas para asistirse en la aritmética. Por ejemplo, dos tablillas encontradas en Senkerah en el Éufrates en 1854, datadas del 200 a. C., dan listas con los números cuadrados perfectos hasta el 59 y con los números cúbicos hasta el 32. Los babilonios usaban las listas de los cuadrados junto a las fórmulas
para efectuar la multiplicación.
Los babilonios no tenían un algoritmo para la división larga, en su lugar basaban su método en el hecho de que
junto con una tabla de recíprocos. Números cuyos únicos factores primos son 2, 3 o 5 (conocidos como números 5-liso o regulares) tienen finitos recíprocos en notación sexagesimal, y se han hallado tablas con extensas listas de estos recíprocos.
Recíprocos tales como 1/7, 1/11, 1/13, etc. no tienen representación finita en notación sexagesimal. Para calcular 1/13 o para dividir un número por 13 los babilonios utilizarían un aproximación tal como
- Raíces cuadradas no exactas fueron aproximadas por el empleo sencillo y reiterado de la media arimético-geométrica ,la que, en la práctica, se obtenía por . [15]
- Para los quebrados propios hubo nombres propios y signos específicos. [16]
- Posibles descubridores del enunciado del teorema de Pitágoras, en sus aplicaciones, conociendo dos elementos de la terna pitagórica, hallaron el tercero mediante una raíz cuadrada, la cual inventaron y aproximaban usando media aritmética ( versión análoga al método de Newton que usa derivadas)[17]
Álgebra
[editar]Así como en cálculo aritmético, los matemáticos babilonios también desarrollaron métodos algebraicos para resolver ecuaciones. Una vez más, estos se basaban en tablas precalculadas.
Para resolver una ecuación cuadrática, los babilonios usaban esencialmente la fórmula cuadrática. Consideraban ecuaciones cuadráticas de la forma
donde aquí b y c no eran necesariamente enteros, pero c siempre era positivo. Sabían que una solución a esta forma de la ecuación es
y utilizarían las tablas de cuadrados en reversa para encontrar raíces cuadradas. Siempre utilizaban la raíz positiva pues esto tenía sentido al resolver problemas «reales». Problemas de este tipo incluía encontrar las dimensiones de un rectángulo dada su área y la cantidad por la cual el largo excedía el ancho.
Tablas de valores de n3 + n2 eran usadas para resolver ciertas ecuaciones cúbicas. Por ejemplo, dada la ecuación
multiplicando la ecuación por a2 y dividiendo por b3 se obtiene
- ;
substituyendo y = ax/b se obtiene
lo cual se puede resolver buscando en la tabla n3 + n2 el valor más cercano al lado derecho. Los babilonios realizaban esto sin notación algebraica, demostrando una remarcable profundidad de entendimiento. No obstante, no poseían un método para resolver la ecuación general de tercer grado.
Modelos de crecimiento
[editar]Los babilonios modelaban el crecimiento exponencial, el crecimiento restringido (vía una forma de funciones sigmoides) y el tiempo doble, esto último dentro del contexto de interés sobre préstamos.
Las tablillas de barro del 2000 a. C. incluyen el ejercicio «dada una tasa de interés de 1/60 por mes (no compuesta), calcular el tiempo doble». Esto da un interés anual de 12/60=20%, y un tiempo doble de 100% crecimiento/20% crecimiento por año = 5 años.[18][19]
Plimpton 322
[editar]La tablilla Plimpton 322 describe un método para resolver lo que hoy en día se describe como funciones cuadráticas de la forma
- ,
por pasos (descritos en términos geométricos) con los que se calculan secuencias de valores intermedios v1 = c/2, v2 = v12, v3 = 1 + v2 y v4 = v31/2, de donde se puede calcular x = v4 + v1 y 1/x = v4 - v1. Las investigaciones de Robson (2001, 2002), publicadas por la Mathematical Association of America,[20] nota que Plimpton 322 puede interpretarse como los valores siguientes, para valores numéricos regulares de x y 1/x en orden numérico:
- v3 en la primera columna,
- v1 = (x - 1/x)/2 en la segunda columna y
- v4 = (x + 1/x)/2 en la tercera columna.
En esta interpretación, x y 1/x habrían aparecido en la tablilla en la parte desprendida, a la izquierda de la primera columna. Por ejemplo, fila 11 de Plimpton 322 puede ser generada de esta forma para x = 2.
Robson señala que Plimpton 322 revela «métodos [matemáticos] ―pares recíprocos, geometría de copiar-y-pegar, completar el cuadrado, dividir por factores comunes regulares― [las cuales] eran todas técnicas simples enseñadas en las escuelas de escribas» de ese tiempo.[21]
La tabla había sido interpretada por matemáticos expertos como una lista de triples pitagóricos y funciones trigonométricas; en 2002 la Mathematical Association of America[20] publicó la investigación de Robson y (en 2003) lo premió con el Lester R. Ford Award por la interpretación moderna rechazando los errores previos.
Geometría
[editar]Los babilonios conocían las reglas usuales para medir volúmenes y áreas. Medían la circunferencia de un círculo como tres veces el diámetro y el área como un doceavo del cuadrado de la circunferencia, lo cual es correcto para una estimación de π a 3. El volumen de un cilindro se calculaba como el producto de la base por la altura, sin embargo, el volumen de un cono truncado o una pirámide cuadrangular se calculaban incorrectamente como el producto de la altura y la mitad de la suma de las bases. El teorema de Pitágoras también les era conocido. Recientes descubrimientos indican que en una tablilla se usaba π como 3 y 1/8. De los babilonios deriva la milla babilónica, una medida de distancia equivalente a siete millas actuales, aproximadamente. Esta medida de distancia se convirtió en la unidad milla-tiempo, utilizada para medir el recorrido del sol, como una representación del tiempo.[22]
Los antiguos babilonios conocieron los teoremas sobre los lados y las razones de triángulos semejantes por muchos siglos, pero desconocían el concepto de medida angular y, consecuentemente, estudiaban los lados de los triángulos en su lugar.[23]
Los astrónomos babilonios mantuvieron un registro detallado de las salidas y las puestas de las estrellas, el movimiento de los planetas, los eclipses solares y lunares; todo lo cual requiere familiaridad con las distancias angulares medidas sobre la esfera celeste.[24]
También utilizaron una forma de análisis de Fourier para calcular efemérides (tablas de posiciones astronómicas), que fue descubierta en los años cincuenta por Otto Neugebauer.[25][26][27][28]
Influencia
[editar]A partir del redescubrimiento de la civilización babilónica, se ha hecho evidente que los matemáticos y astrónomos de la Grecia antigua y del período helenístico tomaron mucho de los babilonios, particularmente Hiparco de Nicea.
Franz Xaver Kugler, en su libro Die Babylonische Mondrechnung (‘el cómputo lunar babilónico’, Friburgo de Brisgovia, 1900) comenta lo siguiente: «Ptolomeo sostenía en su Almagesto IV.2 que Hiparco mejoró los valores de los períodos lunares por él conocidos sobre la base de «astrónomos incluso más antiguos», comparándolos con observaciones de eclipses hechas anteriormente por los caldeos, y por él mismo». Sin embargo, Kugler encuentra que los períodos que Ptolomeo le atribuye a Hiparco ya habían sido utilizados en las efemérides babilónicas, específicamente la colección de textos hoy llamada «Sistema B» (algunas veces atribuido a Kidinnu). Aparentemente Hiparco solo confirma la validez de los períodos que había aprendido de los caldeos, con sus propias observaciones.
Resulta claro que Hiparco (y después Ptolomeo) poseía una lista esencialmente completa de observaciones de eclipses efectuadas durante muchos siglos. Muy probablemente compiladas de las tablillas diarias: estas son tablillas de arcilla en las que se registran todos los eventos relevantes que los caldeos llevaron a cabo rutinariamente. Se preservan ejemplos datados del año 652 a. C. al 130 d. C., pero posiblemente los registros lleguen hasta los días del rey babilonio Nabonasar: Ptolomeo inicia su cronología con el primer día del calendario egipcio del primer año de Nabonasar, o sea el 26 de febrero del 747 a. C.
Esta materia prima por sí sola debe haber sido difícil de aprovechar, y sin duda los caldeos mismos complilaron extractos de los eclipses observados (algunas tablillas con una lista de todos los eclipses registrados durante un período saros han sido halladas). Esto les permitía reconocer la concurrencia periódica de los eventos. Utilizaban, entre otros, en Sistema B (cf. Almagesto IV.2):
- 223 meses sinódicos = 239 vueltas en anomalía (mes anomalístico) = 242 vueltas en latitud (mes draconítico). Conocido hoy como período saros es muy útil para predecir eclipses.
- 251 meses (sinódicos) = 269 vueltas en anomalía
- 5458 meses (sinódicos) = 5923 vueltas en latitud
- 1 mes sinódico = 29;31:50:08:20 días (sexagesimal; 29.53059413… días en decimales = 29 días 12 hr. 44 min. 3⅓ s.).
Los babilonios expresaban todos los períodos en meses sinódicos, debido posiblemente a que utilizaban un calendario lunisolar. Diversas relaciones con eventos anuales determinaban distintos valores para la duración del año.
Similarmente, diversas relaciones entre los períodos del planeta eran conocidos. Las relaciones que Ptolomeo atribuye a Hiparco en el Almagesto IX.3 ya habían sido utilizadas en predicciones halladas en tablillas babilónicas de barro.
Todo este conocimiento fue transferido a los griegos probablemente poco después de las conquistas de Alejandro Magno (331 a. C.). Según el filósofo clásico Simplicio (490-560), Alejandro ordenó la traducción de los archivos astronómicos históricos bajo supervisión de su historiador Calístenes de Olinto (sobrino y discípulo de Aristóteles, a quien se los envió). Cabe la pena mencionar que aunque Simplicio es una fuente tardía, su relato es por demás fiable. Pasó un tiempo exilado en la corte persa sasánida y pudo haber tenido acceso a fuentes desconocidas o perdidas en el Occidente. Llama la atención que haya mencionado el título tèresis (gr. guardia) que es un nombre inusual para un trabajo histórico, pero que de hecho es una traducción adecuada del título babilónico massartu, que significa ‘guardando’ pero también ‘observando’. Como quiera que haya sido, el pupilo de Aristóteles, Calipo de Cícico introdujo su ciclo de 76 años, que mejoró al ciclo metónico de 19 años existente en esa época. El primer año de su primer ciclo comienza en el solsticio de verano del 28 de junio del 330 a. C. (según el calendario juliano proléptico), pero más tarde parece haber contado meses lunares desde el primer mes a partir de la batalla decisiva de Alejandro en Gaugamela en 331 a. C. Calipo pudo haber obtenido sus datos de fuentes babilónicas y su calendario pudo haber sido anticipado por Kidinnu. También es sabido que el sacerdote babilonio Beroso escribió alrededor del año 281 a. C. un libro en griego sobre la (más bien mitológica) historia de Babilonia, la Babyloníaca, para el nuevo gobernante Antíoco I Sóter; se dice que después fundó una escuela de astrología en la isla griega de Cos. Otro candidato para haber enseñado a los griegos sobre astronomía/astrología babilónica es Sudinés, quien era parte de la corte de Atalo I en el siglo III a. C.
En todo caso, la transcripción de los registros astronómicos requería de profundos conocimientos de la escritura cuneiforme, el idioma y los procedimientos, por lo que parece haber sido obra de caldeos desconocidos. Ahora bien, los babilonios databan sus observaciones en su calendario lunisolar, en el cual los meses y los años tenían duraciones diversas (29 o 30 días; 12 o 13 meses respectivamente). En ese tiempo no utilizaban un calendario regular (por ejemplo basado en el ciclo metónico, como hicieron más adelante), e iniciaban un nuevo mes basados en observaciones de la luna nueva. Esto hacía muy tedioso el cómputo de los intervalos de tiempo entre eventos.
Lo que pudo haber hecho Hiparco, es transformar estos registros al calendario egipcio, que utiliza siempre un año fijo de 365 días (formado por 12 meses de 30 días y 5 días extra): esto facilita enormemente los cálculos de intervalos de tiempo. Ptolomeo dató todas las observaciones en este calendario; también escribe: «Todo lo que él (=Hiparco) hizo, fue compilar las observaciones planetarias y ordenarlas más adecuadamente» (Almagesto IX.2). Plinio dice (Naturalis Historia II.IX(53)) sobre las predicciones de eclipses: «Después de su época (=Tales de Mileto) los cursos de ambas estrellas (=Sol y Luna) por 600 años fueron predichos por Hiparco...». Esto parece implicar que Hiparco predijo eclipses por un período de 600 años, pero teniendo en cuenta la enorma cantidad de cálculos requeridos, parece poco probable. Más bien, Hiparco habría hecho una lista de todos los eclipses desde la época de Nabonasar hasta la suya.
Otras trazas de las prácticas babilónicas en el trabajo de Hiparco son:
- primer griego conocido en dividir el círculo en 360 grados de 60 minutos de arco;
- primer uso consistente del sistema de numeración sexagesimal;
- el uso de la unidad pechus (codo), de alrededor de 2° o 2½°;
- uso de un período corto de 248 días = 9 meses anomalísticos.
Bibliografía
[editar]- Berriman, A. E.: The babylonian quadratic equation, 1956.
- Boyer, C. B.: A history of mathematics. Nueva York: Wiley, 2.ª edición revisada por Uta C. Merzbach, 1989. ISBN 0-471-09763-2. Edición en rústica, 1991. ISBN 0-471-54397-7.
- Joseph, G. G., The crest of the peacock. Princeton University Press, 2000. ISBN 0-691-00659-8.
- Joyce, David E.: Plimpton 322, 1995.
- O’Connor, J. J., y E. F. Robertson: «An overview of Babylonian mathematics», en MacTutor History of Mathematics, diciembre de 2000.
- Robson, Eleanor: «Neither Sherlock Holmes nor Babylon: a reassessment of “Plimpton 322”», en Historia Math. 28 (3): págs. 167-206, 2001. DOI 10.1006/hmat.2001.2317. MR 1849797.
- Robson, Eleanor: «Words and pictures: new light on “Plimpton 322”», en The American Mathematical Monthly. Washington: vol. 109, n.º 2; pág. 105, febrero de 2002.
- Robson, Eleanor: Mathematics in Ancient Iraq: a social history. Princeton University Press, 2008.
- Toomer, G. J.: Hipparchus and babylonian astronomy, 1981.
Fuentes
[editar]https://es.wikipedia.org/wiki/Matem%C3%A1tica_babil%C3%B3nica
https://www.um.es/docencia/pherrero/mathis/babilonia/babilon.htm
http://www.profesorenlinea.com.mx/matematica/MatematicaBabilonia.html Las matemáticas de la antigua Grecia tuvieron dos corrientes: la escuela jónica y la escuela pitagórica
Escuela Jónica
[editar]Fue la escuela fundada por Tales de Mileto y estableció cuatro teoremas: 1. “El círculo se bisecta por su diámetro.”
2. “Los ángulos de la base de un triángulo con dos lados iguales son iguales.” (Euc.I, 5). Proclo parece dar a entender que esta afirmación fue demostrada considerando otro triángulo isósceles idéntico, dándole la vuelta y superponiéndolo al primero, una especie de demostración empírica.
3. “Los ángulos opuestos de líneas rectas que se intersectan, son iguales.” (Euc. I, 15). Tales podía haber considerado ésto como obvio, para Proclo fue Euclides el primero que dio una demostración correcta de esta afirmación.
4. “Si dos triángulos son tales que dos ángulos y un lado de uno son iguales a dos ángulos y un lado del otro, entonces los triángulos son congruentes.” (Euc. VI,
Escuela Pitagórica
[editar]Pitagoras atribuyó los siguientes teoremas
Fuentes
[editar]Adaptación de
https://www.um.es/docencia/pherrero/mathis/grecia/grec.htm
https://es.wikipedia.org/wiki/Matem%C3%A1tica_hel%C3%A9nica La matemática india logró una importancia capital en la cultura occidental prerrenacentista con el legado de sus cifras, incluyendo el numeral 0, para escribir el cero: actualmente cardinal del conjunto vacío. Y en numerales polidígitos, el 0 indica que no hay valor alguno en la unidad correspondiente.
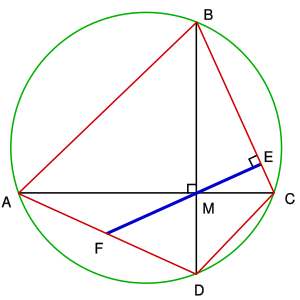
Si bien algunos testimonios permiten opinar que durante la época védica (1500 a.C. a 1000 a.C.) y brahmánica (siglo V) existió en la India una ciencia matemáticas, no obstante fue durante la época clásica (siglos I al VIII) cuando los matemáticos hindúes llegaron a la madurez.
Con anterioridad a este período, los hindúes tuvieron algún contacto con el mundo griego. La marcha de Alejandro Magno sobre la India tuvo lugar durante el siglo IV a.C. Por otra parte, la expansión del budismo en China y la del mundo árabe multiplicaron los puntos de contacto de la India con el exterior. Sin embargo, las matemáticas hindúes se desenvolvieron en un plano original, apoyándose más en el cálculo numérico que en el rigor deductivo.
El mundo les debe el invento trascendental de la notación posicional empleando la cifra cero como valor nulo. Utilizaron, como en occidente, un sistema de numeración de base 10 (decimal, con diez dígitos). Los Antiguos mayas también utilizaron el cero (siglos IV al VII). Egipcios, griegos y romanos, aunque utilizaban un sistema de numeración decimal, no era posicional, ni poseía el cero, que fue transmitido a occidente mucho más tarde, por los pueblos árabes, a través de la España e Italia medievales. Las múltiples ventajas prácticas y teóricas del sistema de «notación posicional con cero» dieron el impulso definitivo a todo el desarrollo ulterior de las matemáticas.
El sistema de numeración decimal aparece ya en el Süryasiddhanta, pequeño tratado que data probablemente del siglo VI y parece que no es muy anterior a éste. Los trabajos matemáticos de los hindúes se incorporaron en general a las obras astronómicas. Este es el caso de Aryabhata, nacido hacia 476, y de Brahmagupta, nacido hacia 598. Mucho más tarde (hacia 1150), Bhaskara II escribió un tratado de aritmética en el que exponía el procedimiento de cálculo de las raíces cuadradas. Se trata de una teoría de las ecuaciones de primer y segundo grado, no en forma geométrica, como lo hacían los griegos, sino en una forma que se puede llamar "algebraica".
El carácter operacional de la matemáticas hindúes iba a la par con una concepción general del número irracional, pero abierta de un modo natural al número negativo, con lo cual podían tomar en consideración los dos signos de la raíz cuadrada y las dos soluciones de la ecuación de segundo grado; así quedó abierto el camino del álgebra formal, seguido posteriormente por los árabes.
Los hindúes fueron los pioneros en utilizar cantidades negativas para representar deudas, ya que en aquellos tiempos notaban la necesidad de representar sus deudas, de tal forma que lo hicieron con el signo(-). EJEMPLO: Para entender mejor la palabra deuda viene de lo que debemos, por decirlo así lo que nos falta y debemos sacar de nuestro bolsillo, pues los hindúes lo representaron con el signo (-).
Los primeros documentos matemáticos hindúes datan del siglo V d.C., sin embargo se piensa que debió haber una actividad matemática mucho antes de esta época. Parte de sus conocimientos geométricos primitivos utilizados en la construcción de templos y altares se encuentran en los salvasutras o "reglas de la cuerda", versiones de conocimientos que pueden remontarse a la época de Pitágoras.
ARITMETICA
NUMERACION DE LA INDIA
La numeración india todavía es usada en india, Pakistán, Bangladesh, Nepal, y Birmania se basa en agrupar dos lugares decimales, en lugar de los tres habituales en casi todo el resto del mundo. Este sistema de numeración nos dio un gran avance ya que introdujo separadores entre los números en los lugares apropiados para el agrupamiento de a dos. Por otra parte en este sistema de numeración aparece el símbolo del cero en el siglo lX, Con la introducción del símbolo para el 0 de la numeración hindú tenemos el sistema de numeración que actualmente usamos. Con una base decimal, una notación posicional, una forma cifrada para cada uno de los diez numerales básicos. La suma y la multiplicación se hacían en la India casi como las hacemos hoy, salvo porque la escritura de los números se hacía con los de orden menor a la izquierda. Para multiplicar 456 x 34 = 15.504 lo hacían de la siguiente manera. La disposición en celdillas es un recurso para evitar las "llevadas", sólo hay que tener en cuenta las llevadas de las sumas parciales diagonalmente
GEOMETRÍA
Entre las obras relacionadas con la geometría esta los aryabhata, siddhantas, y los sulvasutras en la última nos encontramos con reglas para la construcción de ángulos rectos por medio de ternas, cuyas longitudes constituyen a ternas pitagóricas, para la construcción de altares. Pero sin embargo se cree que esta reglas fueron heredaron de los babilonios. También agregó a este libro algunos aportes de los elementos de Euclides. Pero se cree que estas obras fueron basadas en obras de los matemáticos griegos. Los sulvasutras también contenía temas relacionados con la aritmética (fracciones, raíces cuadradas, interés simple, la regla de tres, la regula fácil) y álgebra (ecuaciones lineales y cuadráticas) y progresiones aritméticas। También contiene problemas geométricos.
TRIGONOMETRIA
Una de las contribuciones de la india a las matemáticas, consistió en la función equivalente al seno en trigonometría, para remplazar las tablas de cuerdas griegas las tablas más antiguas son las encontradas en los siddhantas y en el aryabhata donde se dan los senos de los ángulos menores de 90 grados 0, se tomaba como radio 3,438 unidades y la circunferencia correspondía como 360 *60=21600 unidades, pero para los hindúes en ecuaciones p era la raíz cuadrada de 10।
ALGEBRA
En la matematica de la india se destacaron cuatro nombres propios: Aryabhata (s।VI), Brahmagupta (s।VI), Mahavira (s. IX) y Bhaskara Akaria (s.XII) quienes Profundizaron en la obtención de reglas de resolución de ecuaciones lineales y cuadráticas, en las cuales las raíces negativas eran interpretadas como deudas. Desarrollaron también, sin duda para resolver problemas astronómicos, métodos de resolución de ecuaciones diofánticas, llegando incluso a plantear y resolver (siglo XII) la ecuación x²=1+ay², denominada ecuación de Pelt. ARITMÉTICA SISTEMA DE NUMERACIÓN
En china existieron 2 sistemas de numeración en uno los números se representaban por pequeñas varillas de bambú o marfil, este sistema perduro muy poco, ya que se creaban problemas de confusión entre las descripciones de números grandes. El problema más grande con esta notación fue que podría llevar a una confusión. ¿Qué era ? Podría ser 3, o 21 o 12 o incluso 111.
El otro sistema es de la forma clásica que a usar desde el 1500 A.C. aproximadamente. Es un sistema decimal estricto que usa las unidades con símbolo distinto para cada uno de ellos. En este sistema de numeración era fundamental el orden de la escritura ya que 5 10 7 igual podría representar 57 que 75.
Los eruditos chinos por su parte desarrollaron un sistema posicional muy parecido al actual que desde que incorporó el cero por influencia india en s। VIII en nada se diferencia de este।
EL ÁBACO
Con esta gran herramienta que se inventaron los chinos y que aun se utiliza, los chinos implementaron su forma de hacer las operaciones básicas en el ábaco nos lo han heredado los chinos conocían bien las operaciones con fracciones ordinarias hasta el puno de que hallaban el mínimo común denominador de varias fracciones, con las fracciones hacían analogías entre sexos, refiriéndose al denominador como “el hijo” y al denominador como “la madre “también utilizaban el yin y yang aparte de esto adoptaron un sistema decimal en pasos y medidas dio como resultado como resultado la implementación de decimales en el manejo de las fracciones.
Después de esto los chinos descubrieron la idea de los números negativos, no les causo muchas dificultades ya que estaban acostumbrados a calcular usando las varillas, uno de color rojo para los positivos y de color negro para los negativos. aunque nunca los aceptaron como solución a una ecuación.
LOS CUADRADOS MAGICOS
Los chinos han sido siempre muy aficionados al diseño armónico, aritmético o geométrico, estos cuadraditos ayudaron al autor de los nueve capítulos a resolver el sistema de ecuaciones lineales. Estos cuadros y diferentes figuras consistía en que en todos sus lados diera el mismo número
GEOMETRÍA en la matemática primitiva de china se ve que quizá dependió un poco de Mesopotamia ya que tenían el mismo valor para p(3), en la búsqueda de valores más exactos, aparece liu hui de donde se obtiene el valor de 3,14usando un polígono regular de 96 lados y la aproximación mejor de 3,14159
TRIANGULO ARITMETICO Las obras de yang hui incluían también otros resultados para la suma de series finitas y del llamado triangulo de pascal, pero también son conocidas en el espejo precioso publicado por chu shih-shih, quien maneja estas sumas por medio del método de diferencias finitas y por otra parte el teorema binomial para potencias enteras positivas
ALGEBRA De la época de la primera dinastía Han (206 a. C. hasta 24 d.C.) procede el tratado Matemáticas en nueve Libros. Posteriormente otros matemáticos como Liu Hui (siglo III), Sun-zi (siglos II-IV), Liu Zhuo (siglo VI) y otros hicieron aportaciones a este tratado. El texto trata problemas económicos y administrativos como medición de campos, construcción de canales, cálculo de impuestos,..Trabajan las ecuaciones lineales indeterminadas y un procedimiento algorítmico para resolver sistemas lineales parecidos al que hoy conocemos como método de Gauss que les llevó al reconocimiento de los números negativos. Estos números constituyen uno de los principales descubrimientos de la matemática china.
La escuela algebraica china alcanza su apogeo en el siglo XIII con los trabajos de Quin Jiu-shao, Li Ye, Yang Hui y Zhu Shi-jie que idearon un procedimiento para la resolución de ecuaciones de grado superior llamado método del elemento celeste o tian-yuanshu. Este método actualmente se conoce como método de Horner matemático que vivió medio milenio más tarde.
El desarrollo del álgebra en esta época es grandioso: sistemas de ecuaciones no lineales, sumas de sucesiones finitas, utilización del cero, triángulo de Tartaglia (o Pascal) y coeficientes binomiales así como métodos de interpolación que desarrollaron en unión de una potente astronomía.
El siglo VII vió la enorme gesta de ingeniería que supuso la unión de los dos ríos más importantes de China mediante el Gran Canal de 1700 km. de largo. Muhamad ibn Musa al-Kuarizmi. El imperio islámico, establecido a lo largo del Oriente Medio, Asia Central, África del Norte, Iberia, y parte de la India, hizo aportes significativos en matemáticas en el siglo octavo. Aunque la mayor parte de los textos islámicos sobre matemáticas fueron escritos en árabe, no todos fueron escritos por árabes, dado que, así como el griego era usado en el mundo helenístico, el árabe era usado como el lenguaje escrito de los intelectuales no árabes a lo largo del mundo islámico en aquella época. Junto con los árabes, muchos otros importantes matemáticos islámicos fueron persas.
En el siglo IX, Al-Juarismi escribió varios libros importantes sobre los números arábigos y sobre los métodos de resolución de ecuaciones. Su libro Sobre los cálculos con números arábigos, escrito alrededor del año 825, junto con el trabajo de Al-Kindi, fueron instrumentos para dar a conocer las matemáticas árabes y los números arábigos en Occidente. La palabra algoritmo se deriva de la latinización de su nombre, Algoritmi, y la palabra álgebra del título de uno de sus trabajos, Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa’l-muqābala (Compendio de cálculo por compleción y comparación). Al-Juarismi a menudo es apodado "el padre del álgebra", por sus importantes contribuciones a este campo.Aportó una meticulosa explicación a la solución de ecuaciones de segundo grado con raíces positivas, y fue el primero en enseñar el álgebra en sus formas más elementales. También introdujo el método fundamental de "reducción" y "balance", refiriéndose a la colocación de los términos restados al otro lado de una ecuación, es decir, la cancelación de términos iguales que se encuentran en lados opuestos de una ecuación. Esta operación fue descrita originariamente por Al-Jarismi como al-jabr. Su álgebra no solo consistía "en una serie de problemas sin resolver, sino en una exposición que comienza con las condiciones primitivas que se deben dar en todos los prototipos de ecuaciones posibles mediante una serie de combinaciones, a partir de este momento serán objeto de estudio."
El posterior desarrollo del álgebra vino de la mano de Al-Karaji. En su tratado al-Fakhri extiende la metodología para incorporar potencias y raíces de cantidades desconocidas. La primera demostración por inducción matemática de la que se tiene constancia aparece en un libro escrito por Al-Karaji en el 1000 d.C., en el que demuestra el teorema del binomio, el triángulo de Pascal, y la suma de cubos integrales.El historiador de las matemáticas, F. Woepcke,elogió a Al-Karaji por haber sido "el primero en introducir la teoría del cálculo algebraico." También en el siglo X Abul Wafa tradujo las obras de Diofanto al árabe y desarrolló la función tangente. Ibn al-Haytham fue el primer matemático en deducir la fórmula de la suma de las ecuaciones cuárticas, usando un método que puede generalizarse para determinar la fórmula general de la suma de cualquier potencia entera. Desarrolló una integración para calcular el volumen de un paraboloide y fue capaz de generalizar sus resultados para las integrales de polinomios de más de cuarto grado. Incluso se acercó bastante a la fórmula general de la integral de polinomios, aunque no estaba interesado en polinomios de grado mayor que cuatro.
En las postrimerías del siglo XI, Omar Khayyam escribió Discusiones sobre las dificultades en Euclides, un libro sobre los defectos en los Elementos de Euclides, especialmente el postulado de las paralelas, y estableció los fundamentos de la geometría analítica y la geometría no euclídea. También fue el primero en encontrar la solución geométrica a la ecuación cúbica e influyó en la reforma del calendario.
Los números que llamamos árabes no son árabes sino hindúes; pero la mayoría de la gente cree, erróneamente, que los números que utiliza son árabes.
Tampoco las cifras que utilizamos son originales de los árabes: si se observa la grafía hindú del siglo VI se puede comprobar que es muy similar a la nuestra.
Después de un siglo de expansión en la que la religión musulmana se difundió desde sus orígenes en la península Arábiga hasta dominar un territorio que se extendía desde la península Ibérica hasta los límites de la actual China, los árabes empezaron a incorporar a su propia ciencia los resultados de "ciencias extranjeras".
Los traductores de instituciones como la Casa de la Sabiduría de Bagdad, mantenida por los califas gobernantes y por donaciones de particulares, escribieron versiones árabes de los trabajos de matemáticos griegos e indios.
Hacia el año 900, el periodo de incorporación se había completado y los estudiosos musulmanes comenzaron a construir sobre los conocimientos adquiridos.
El sistema hindú era, al contrario del griego o romano, de carácter "posicional". Lo que significa que las cifras tiene diferente valor según el lugar que ocupan. Entre otros avances, los matemáticos árabes ampliaron el sistema indio de posiciones decimales en aritmética de números enteros, extendiéndolo a las fracciones decimales.
Para los romanos V era siempre cinco estuviera colocado en una posición o en otra (V I I= 5+1+1=7; VI = 5+1=6), mientras que para nosotros, y mucho antes para los hindúes, en el número 511 el cinco vale quinientos mientras que en el 51 vale cincuenta. Esta idea que hoy nos puede parecer tan elemental los grandes matemáticos griegos no la tuvieron y sin embargo se tiene constancia de que en el siglo VI los hindúes no sólo la utilizaban en su sistema de numeración sino que además manejaban con soltura las cuatro reglas y el cero.
El gran mérito atribuible, pues, a los árabes es el de haberse dado cuenta de las ventajas que el sistema hindú tenía sobre todos los demás.
Cuando se habla de matemática árabe no se suele tener en cuenta, además, que muchos de los científicos de los que se habla eran persas, judíos e incluso cristianos.
En el siglo XII, el matemático persa Omar Khayyam generalizó los métodos indios de extracción de raíces cuadradas y cúbicas para calcular raíces cuartas, quintas y de grado superior.
El más conocido de los matemáticos árabes es Mohammed Ibn Musa Al-Khwarizmi (780-850), conodido como padre del álgebra.
Se sabe poco de su vida salvo que vivió en la primera mitad del siglo IX y que trabajó en la biblioteca del califa de Bagdad.
Escribió libros sobre geografía, astronomía y matemática. En su obra Aritmética ("Algoritmi de numero indorum") explica con detalle el funcionamiento del sistema decimal y del cero que usaban en la India. Obra de gran importancia pues contribuyó a la difusión del sistema de numeración indio y al conocimiento del cero.
Debe destacarse la obra de contenido algebráico "Hisab al-yabr wa'l muqqabala", considerada uno de los primeros libros de álgebra. Obra eminentemente didáctica con abundantes problemas para resolver y adiestrar al lector, principalmente, en la resolución de ecuaciones de segundo grado.
Es el autor de uno de los métodos más antiguos que se conocen para resolver ecuaciones de segundo grado. Dicho método, geométrico, se conoce como de completar cuadrado.
Los geómetras, como Ibrahim ibn Sinan, continuaron las investigaciones de Arquímedes sobre áreas y volúmenes. Kamal al-Din y otros aplicaron la teoría de las cónicas a la resolución de problemas de óptica. Los matemáticos Habas al-Hasib y Nasir ad-Din at-Tusi crearon trigonometrías plana y esférica utilizando la función seno de los indios y el teorema de Menelao. Estas trigonometrías no se convirtieron en disciplinas matemáticas en Occidente hasta la publicación del De triangulis omnimodis (1533) del astrónomo alemán Regiomontano.
Finalmente, algunos matemáticos árabes lograron importantes avances en la teoría de números, mientras otros crearon una gran variedad de métodos numéricos para la resolución de ecuaciones.
Los países europeos con lenguas latinas adquirieron la mayor parte de estos conocimientos durante el siglo XII, el gran siglo de las traducciones.
Los trabajos de los árabes, junto con las traducciones de los griegos clásicos fueron los principales responsables del crecimiento de las matemáticas durante la edad media. Los matemáticos italianos, como Leonardo Fibonacci y Luca Pacioli (uno de los grandes tratadistas del siglo XV en álgebra y aritmética, que desarrollaba para aplicar en el comercio), se basaron principalmente en fuentes árabes para sus estudios.
La matemática islámica desarrolló principalmente la aritmética decimal con fracciones decimales, que tomó de los hindúes, el álgebra, la
trigonometría plana y esférica y la resolución numérica de ecuaciones y de sistemas de ecuaciones. Mucho de este desarrollo vino estimulado por uno de los grandes problemas de la astronomía y geodesia árabe, el de la qibla (o kibla), de deteminar la dirección a la Meca hacia donde debían mirar los creyentes durante sus oraciones. Entre los matemáticos más destacados están al-Kwarizmi (780-850), ibn al-Haytham (conocido en europa como Alzacén) (965-1039), al-Khayyami (1048-1131), al-Biruni (973-1055) y al-Kashi (1380-1429). De al-Kwarizmi, miembro de la casa de la sabiduría, viene la palabra "algoritmo". La palabra "álgebra" proviene de "al-jabr", de la frase "al-jabr wa al-muqabala", que Kwarizmi utilizaba en sus escritos, "al-jabr" significa "trasponer" (de un lado al otrode la igualdad cambiando de signo), "wa" es " y", mientras que "al-muqabala" significa "simplificar". Por ejemplo al pasar de 3x+2=4-2x a 5x+2=4 es un ejemplo de "al-jabr", mientras que pasar de esta última a 5x=2 es "al-muqabala". Fue en Europa a partir del siglo XVII cuando se establecieron las herramientas necesarias para el desarrollo de las matemáticas, principalmente el análisis. Algunos matemáticos importantes importantes son:
- François Viète (1540-1603): es el padre de la primera formalización algebraica.
- René Descartes (1596-1650): es el fundador de la geometría analítica y del plano cartesiano.
- Pierre de Fermat (1607-1665): planteó varios teoremas y creo la teoría de la probabilidad discreta junto con Pascal.
- Isaac Newton (1642-1727): Se le debe el nacimiento del cálculo infinitesimal.
- Leonhard Euler (1707-1783): Sienta las bases teóricas de muchas disciplinas matemáticas: topología, números complejos, series infinitas, entre otras.
- Carl Friedrich Gauss (1777-1855): Crea varias generalizaciones y nuevas herramientas en diversos campos siendo el primero en demostrar rigurosamente cualquier afirmación matemática.
- Augustin Louis Cauchy (1789-1857): Sus aportes teóricos en análisis permiten aclarar y hacer más rigurosa esta rama matemática.
- Évariste Galois (1811-1832): Sentó las bases de la teoría de grupos.
- Arthur Cayley (1821-1895): Realizo trabajos sobre matrices y teoría de grupos.
- Bernhard Riemann (1826-1866): Aportó notablemente en la geometría diferencial.
- Georg Cantor (1845-1918): Creó la teoría de conjuntos y propuso los números infinitos.
- Henri Poincaré (1854-1912): Sus avances en el problema de los tres cuerpos lo llevan a la teoría del caos.
- David Hilbert (1862-1943): Influyó mucho en las matemáticas modernas, especialmente con sus 23 problemas.
Enlaces
[editar]http://wordpress.colegio-arcangel.com/matematicas
http://www.profesorenlinea.com.mx/matematica/MatematicaHistoria.htm
http://www.sectormatematica.cl/historia.htm
http://platea.pntic.mec.es/~jdelucas/losmatematicos.htm
https://www.um.es/docencia/pherrero/mathis/
http://marlyforeroblogspotcom.blogspot.mx/
https://sites.google.com/site/historiadelamatematicaperu2016/home
http://www.mat.uson.mx/depto/publicaciones/apuntes/
https://www.uam.es/personal_pdi/ciencias/fchamizo/realquiler/fich/apuntesHM.pdf
- ↑ Ian Stewart, Historia de las matemáticas, Crítica, 2008. ISBN 978-84-8432-369-3 p. 12-13
- ↑ Ian Stewart, Historia de las matemáticas, Crítica, 2008. ISBN 978-84-8432-369-3 p. 14
- ↑ Hofmann. «Historia de la matemática»
- ↑ Hofmann. Op. cit.
- ↑ H. Lewy: «Studies in assyro-babylonian mathematics and metrology», en Orientalia (NS) 18, 40-67; págs. 137-170, 1951.
- ↑ Lewy, H. (1951 «Studies in assyro-babylonian mathematics and metrology», en Orientalia (NS) 20, págs. 1-12.
- ↑ E. M. Bruins: «La classification des nombres dans les mathématiques babyloniennes», en Revue d'Assyriologie, 47, págs. 185-188, 1953.
- ↑ Cazalas: «Le calcul de la table mathématique AO 6456», en Revue d'Assyriologie 29, págs. 183-188, 1932.
- ↑ S. Langdon: «Assyriological notes: mathematical observations on the Scheil-Esagila tablet», en Revue d'Assyriologie 15, págs. 110-112, 1918.
- ↑ E. Robson: «Guaranteed genuine originals: the Plimpton Collection and the early history of mathematical assyriology», en Mining the archives: Festschrift for Chrisopher Walker on the occasion of his 60th birthday (ed. C. Wunsch). ISLET, Dresden, págs. 245-292, 2002.
- ↑ 11,0 11,1 Asger AABOE: «The culture of Babylonia: babylonian mathematics, astrology, and astronomy», en John Boardman, I. E. S. Edwards, N. G. L. Hammond, E. Sollberger y C. B. F. Walker (eds.): The assyrian and babylonian empires and other states of the Near East, from the eighth to the sixth centuries B. C. Cambridge University Press, 1991.
- ↑ Bell: Historia de las matemáticas
- ↑ Hofmann. «Historia de la matemática»
- ↑ Duncan J. Melville: «Third millennium chronology», en Third millennium mathematics. St. Lawrence University, 2003.
- ↑ Hofmann. «Historia de la matemática» Limusa Noriega Editores, México, D.F. (2003)
- ↑ Hofmann. Op. cit.
- ↑ Boyer "Historia de la matemática"
- ↑ Michael Hudson: «Why the “miracle of compound interest” leads to financial crises», 2007.
- ↑ John H. Webb: «Have we caught your interest?»
- ↑ 20,0 20,1 Véase el artículo «Mathematical Association of America» (en inglés) en la Wikipedia en inglés.
- ↑ Robson, American Mathematical Monthly, págs. 117-118, 2002.
- ↑ Eves, capítulo 2.
- ↑ Boyer: «Greek trigonometry and mensuration» (págs. 158-159), 1991.
- ↑ Eli Maor: Trigonometric delights. Princeton University Press, 1998. ISBN 0691095418.
- ↑ Elena Prestini: The evolution of applied harmonic analysis: models of the real world (pág. 62). Birkhäuser, 2004. ISBN 978 0 81764125 2.
- ↑ Gian-Carlo Rota; y Fabrizio Palombi: Indiscrete thoughts (pág. 11). Birkhäuser, 1997. ISBN 978 0 81763866 5.
- ↑ Otto Neugebauer: The exact sciences in antiquity. [1957]. Dover Publications, 2.ª edición, 1969. ISBN 978-048622332-2.
- ↑ Lis Brack-Bernsen y Matthias Brack: Analyzing shell structure from babylonian and modern times. Physics/0310126.
