1. INTRODUCTION
Precise Point Positioning (PPP) is a rapidly growing positioning technique in Global Navigation Satellite System (GNSS). PPP can achieve positioning accuracy of decimetre- to centimetre-level when dual-frequency GNSS observations are used in conjunction with correction data from precise satellite orbit and clock products (Zumberge et al., Reference Zumberge, Heflin, Jefferson, Watkins and Webb1997; Kouba and Héroux, Reference Kouba and Héroux2001). Over the past decade, the dual-frequency PPP technique has been developed rapidly. Recently single-frequency PPP has also attracted great attention (see e.g. Øvstedal, Reference Øvstedal2002; Héroux et al., Reference Héroux, Gao, Kouba, Lahaye, Mireault, Collins, Macleod, Tétreault and Chen2004; Gao et al., Reference Gao, Zhang and Chen2006; Le and Tiberius, Reference Le and Tiberius2007; Bock et al., Reference Bock, Jäggi, Dach, Schaer and Beutler2009; van Bree and Tiberius, Reference van Bree and Tiberius2011; Odijk et al., Reference Odijk, Teunissen and Zhang2012). This evolution significantly expands the usability of PPP technique in a much broader range of GNSS applications. Since the majority of mass-market GNSS users are still operating single-frequency receivers due to the low costs, development of the single-frequency PPP technique is of great interest in the GNSS community.
The greatest challenge for single-frequency PPP is the treatment of ionospheric delay – a major error source in GNSS, though it is not a problem in dual-frequency PPP. Basically, there are two approaches to handling the ionospheric delay in single-frequency PPP. One is to apply ionospheric models to mitigate the ionospheric effect. The second is to form a single-frequency ionosphere-free observable using pseudorange and carrier phase observations on the L 1 frequency, which is known as GRoup And PHase Ionospheric Correction (GRAPHIC) (Yunck, Reference Yunck, Parkinson and Spilker1996).
Øvstedal (Reference Øvstedal2002) demonstrates the improvement in single-frequency PPP results using the Global Ionosphere Maps (GIM) ionospheric model compared to the Klobuchar model (Klobuchar, Reference Klobuchar1987). As the accuracy of the GIM model is limited to 2–8 TECU (i.e. 0·32–1·28 m for GPS L 1 frequency), the pseudorange-based PPP positioning accuracy is only approximately one metre. Le and Tiberius (Reference Le and Tiberius2007) demonstrate a further accuracy improvement using a carrier phase-based pseudorange filtering algorithm. Based on predicted GIM, real-time single-frequency PPP has also been developed with a positioning accuracy of several decimetres (van Bree et al., Reference van Bree, Tiberius and Hauschild2009; van Bree and Tiberius, Reference van Bree and Tiberius2011). Instead of using the GIM model, an ionospheric estimation model that takes ionospheric gradients into account has also been used for real-time single-frequency PPP at a comparable accuracy level (Chen and Gao, Reference Chen and Gao2005; Gao et al., Reference Gao, Zhang and Chen2006). In summary, the present single-frequency PPP technique can achieve only metre to several decimetres accuracy if ionospheric models are used to mitigate the ionospheric effect. Muellerschoen et al. (Reference Muellerschoen, Iijima, Meyer, Bar-Sever and Accad2004) evaluated the real-time single-frequency PPP performance based on the GRAPHIC method using data from globally distributed ground stations. Decimetre-level positioning accuracy has been achieved. For static single-frequency PPP, an accuracy of several centimetres may be obtained after undergoing a long convergence time of over two hours (Héroux et al., Reference Héroux, Gao, Kouba, Lahaye, Mireault, Collins, Macleod, Tétreault and Chen2004). Such a long convergence time is needed because the noise level of the GRAPHIC combination observables is dominated by the noise of the pseudorange measurements.
In order to reduce the convergence time and improve the positioning accuracy of single-frequency PPP, we propose the integration of GPS and GLONASS signals and so utilise the benefit of having both satellite systems. In the past, most single-frequency PPP work was done with GPS signals. For the combined GPS/GLONASS PPP, much work using dual-frequency observations has been done by several researchers and their results have shown improved performances over GPS-only PPP solutions (Cai and Gao, Reference Cai and Gao2007; Hesselbarth and Wanninger, Reference Hesselbarth and Wanninger2008; Píriz et al., Reference Píriz, Calle, Mozo, Navarro, Rodríguez and Tobías2009; Melgard et al., Reference Melgard, Vigen, Jong, Lapucha, Visser and Oerpen2009; Cai and Gao, Reference Cai and Gao2012). In this paper, we focus on the GPS/GLONASS Single-Frequency (GGSF) PPP because a larger GPS/GLONASS user community can benefit as the single-frequency PPP technique evolves. In addition, the recent revitalization of the GLONASS system provides great opportunity for the GPS/GLONASS users. The GLONASS constellation at present consists of 24 fully operational healthy satellites and provides global coverage. More satellites are expected to be launched in the forthcoming years. In this GGSF PPP, the GRAPHIC combination is used to remove the ionospheric delay. Different types of precise satellite orbit and clock products are used to analyse the positioning results. Datasets collected from 22 globally distributed International GNSS Service (IGS) stations were processed in three independent sessions to assess the performance of the GGSF PPP. A kinematic test was also carried out to analyse the achievable accuracy of GGSF PPP in a kinematic mode. Statistical results indicate that both static and kinematic GGSF PPP can significantly improve convergence time and positioning accuracy over the GPS-only or GLONASS-only single-frequency PPP.
2. APPROACHES FOR COMBINED GPS/GLONASS SINGLE-FREQUENCY PPP
For a GLONASS satellite r, the pseudorange and carrier phase observations on the L 1 frequency between a receiver and a satellite can be expressed as:
where:
P is the measured pseudorange in metres.
φ is the measured carrier phase in cycles.
ρ is the geometric range in metres.
c is the speed of light in metres per second.
dt R is the GLONASS receiver clock offset in seconds.
dT is the satellite clock offset in seconds.
d orb is the satellite orbit error in metres.
d trop is the tropospheric delay in metres.
d ion is the ionospheric delay in metres.
λ is the wavelength for a GLONASS satellite r in metres per cycle.
N is the phase ambiguity in cycles.
ε P includes the pseudorange multipath error and pseudorange noise in metres.
ε φ includes the carrier phase multipath error and carrier phase noise in metres.
Considering that some biases, such as the hardware delay bias, contained in the pseudorange and carrier phase measurements will be absorbed into the receiver clock offset and phase ambiguity items in the parameter estimation, they are not included in the above observation equations. Combining (1) and (2), the ionosphere-free combined observables may be obtained as:
Similarly, the GPS ionosphere-free combined observables on the L 1 frequency may be expressed as:
where:
g represents a GPS satellite.
dt G is the GPS receiver clock offset in seconds.
λ is the GPS wavelength in metres per cycle.
ε IF includes the multipath error and noise of ionosphere-free combined observables in metres.
The single-frequency ionosphere-free combination makes use of the fact that pseudorange and carrier phase measurements from the same satellite undergo ionospheric delay of the same magnitude but opposite sign. The GLONASS receiver clock offset dt R may be expressed as the sum of the GPS receiver clock offset dt G and the GPS-GLONASS system time difference dt sys (Cai and Gao, Reference Cai and Gao2012). After applying the GPS and GLONASS precise satellite orbit and clock corrections, as well as other error corrections that need to be considered in PPP (Kouba and Héroux, Reference Kouba and Héroux2001), Equations (3) and (4) may be written as:
The GGSF PPP observation model consists of Equations (5) and (6). The unknown parameters include three station coordinates, one receiver clock offset dt G, one GPS-GLONASS system time difference dt sys, one zenith tropospheric delay, and L 1 carrier phase ambiguities for all the tracked GPS and GLONASS satellites. These parameters can be modelled in a Kalman filter similar to that in dual-frequency PPP (Cai and Gao, Reference Cai and Gao2012). It is worthy of notice that the noise level of the ionosphere-free observables is dominated by the noise of the pseudorange measurements. The large noise in the observables has an impact on the positioning convergence time.
3. GGSF PPP SOLUTION ANALYSIS USING DIFFERENT PRECISE PRODUCTS
In the derivation of ionosphere-free combined observable Equations (5) and (6), the satellite orbit and clock errors are assumed to have been corrected using precise satellite orbit and clock products. In order to evaluate their effects on the GGSF PPP solutions, different types of such products from both the Information – Analytical Centre, Russia (IAC) and the European Space Operations Centre, Germany (ESA/ESOC) were applied to estimate the GGSF PPP solutions. GPS and GLONASS orbit products can also be obtained from IGS. However, the satellite clock products are only available from IAC and ESA/ESOC (Hesselbarth and Wanninger, Reference Hesselbarth and Wanninger2008). According to the difference in latency, both IAC and ESA/ESOC provide different types, including: final, rapid and ultra-rapid products. Their latencies vary from several hours to a few days. IAC offers final satellite clock corrections at two types of intervals, i.e. 5 minutes and 30 seconds. But the final clock corrections from ESA/ESOC are provided only at a 30 s interval.
A 3 h dataset collected at IGS station LCK2 on 1 June 2012 was randomly selected from the IGS tracking network for GGSF PPP processing. The station is located in Lucknow, India. The dataset has a sampling interval of 30 s. The elevation mask angle is set to 15° in the data processing. For the Kalman filter, the spectral density values for the tropospheric zenith wet delay, GPS receiver clock offset (in units of metres) and system time difference parameter (in units of metres) are empirically set to 10−9 m2/s, 105 m2/s and 10−7 m2/s, respectively. The initial Standard Deviation (STD) values are empirically set to 0·3 m for code observations and 0·002 m for phase observations for both GPS and GLONASS. IGS weekly coordinate solutions are used as references to calculate positional errors in East, North and Up directions. The antenna model ‘‘igs08.atx’’ is used for both satellite and receiver antenna phase centre corrections (IGSMAIL-6384).
Figures 1 and 2 show the GGSF PPP results using the IAC and ESA/ESOC precise products, respectively. Figure 1 illustrates that the GGSF PPP solutions are of almost the same accuracy when different types of IAC precise orbit products and 5 minute clock corrections are used. The use of higher-rate (30 s) IAC satellite clock correction data has only a little impact on the positioning performance. Figure 2 shows slightly different positioning results obtained from using different types of ESA/ESOC products. In the analysis of positioning accuracy, only the solutions after convergence are considered. In this study, the positioning solution convergence criterion is defined as positioning errors smaller than 0·15 m in the East and North directions and 0·3 m in the vertical direction. When using the ultra-rapid IAC and ESA/ESOC products in GGSF PPP, the positioning solutions start to converge at the 253rd (126·5 min) and 276th (138 min) epochs, respectively. The Root Mean Square (RMS) statistical results shown in Table 1 indicate that the accuracies in the East and North directions for all IAC and ESA/ESOC products are better than 6 cm and 3 cm, respectively. The vertical accuracy is better than 20 cm even for the ultra-rapid products. Please note that in Table 1, for comparison purposes, the statistics for all the IAC products are calculated uniformly using positioning solutions after 126·5 min, although the positioning solution of final orbit gets converged earlier. Similarly, the statistics for ESA/ESOC products use solutions after 138 min. As expected, the use of the rapid or ultra-rapid precise products indeed degraded the three-dimensional positioning accuracy due to the reduced accuracy of the orbit and clock products compared with the final products. The three-dimensional positioning accuracy is at one-decimetre-level using the final orbit and 30 s clock products from IAC or ESA/ESOC. When the IAC or ESA/ESOC precise products are used for GPS-only, or GLONASS-only, single-frequency PPP processing, the outcomes are similar to those illustrated in Figures 1 and 2. Only slight differences in the positioning errors are found using the different latencies of precise products.

Figure 1. Positioning errors of GGSF PPP at LCK2 station using different IAC precise products.

Figure 2. Positioning errors of GGSF PPP at LCK2 station using different ESA/ESOC precise products.
Table 1. RMS statistics of positioning errors using different precise products (m).

Figure 3 shows a comparison between GGSF and GPS/GLONASS dual-frequency PPP solutions using the IAC final orbit products and 30 s clock corrections. The GGSF PPP takes much longer than the dual-frequency PPP before its positioning solutions converge. The position filter for GGSF PPP needs 112 minutes to converge in all three directions while it needs only 10 minutes for dual-frequency PPP. This is due to the much weaker observation model when based on single-frequency ionosphere-free observables. The RMS values of converged position errors are 0·027, 0·036 and 0·039 m for dual-frequency PPP and 0·032, 0·008 and 0·149 m for GGSF PPP in the East, North and Up directions, respectively. This indicates that the PPP can achieve a positioning accuracy comparable to the dual-frequency PPP, especially in the horizontal directions.

Figure 3. Single-frequency vs. dual-frequency PPP position errors using combined GPS and GLONASS observations at LCK2 station on 1 June 2012.
4. GGSF PPP SOLUTION ANALYSIS USING KINEMATIC DATA
A kinematic experiment was conducted on 17 December 2011 at an open-sky area close to the East gate of the new campus of Central South University (CSU), Changsha, China. Figure 4 shows the setup of the base and rover receivers, both of which are GNSS dual-frequency receivers manufactured by Hi-Target Inc. in Guangzhou, China. The base receiver was set up on the roof of the Mining Building at the CSU. The rover receiver was mounted on an electric motorcycle that ran repeatedly along a nearly rectangular trajectory with a width of 150 m and a length of 250 m. The test lasted approximately 2 hours, starting from local time 16:45:00 (UTC+8 h) and ending at local time 18:46:00. The data were collected at a sampling rate of 1 Hz. An elevation mask angle of 15 degrees was set and only the observations on the L 1 frequency were used for PPP processing. Dual-frequency observations at base and rover stations were processed in a post-mission mode using the double difference Real-Time Kinematic (RTK) approach. The RTK solutions were then used as reference coordinates to evaluate the GGSF PPP kinematic solutions. In the Kalman filter of GGSF data processing, a ‘random walk’ process was used to model the dynamics of the vehicle with a spectral density value of 102 m2/s. The spectral density values for other parameters were same as the static case. The IAC final precise satellite orbit and 30 s clock products were used to estimate the coordinates of the rover station on an epoch-by-epoch basis.

Figure 4. Setup of base and rover stations.
Figure 5 shows the positioning errors of the GPS-only, GLONASS-only and the combined GPS/GLONASS single-frequency PPP solutions with respect to the reference coordinates. The positioning errors in all three components from the GGSF are significantly smaller than those obtained from GPS, or GLONASS, alone. It is of note that the positioning errors for GLONASS-only are much larger than those for GPS-only. This can be explained by the smaller number of GLONASS satellites and worse satellite geometry as shown in Figure 6. Figure 6 indicates that the combination of GPS and GLONASS has resulted in great benefit over a single system in terms of the number of satellites and satellite geometry. Between 1815th and 5445th epochs, the GLONASS Position Dilution of Precision (PDOP) is much worse than that of GPS. However from 6182nd to 7260th epochs, the GPS PDOP is considerably worse than that of GLONASS. A large PDOP value results in poor positioning accuracy, especially for the vertical component, as shown in the bottom panel of Figure 5. The combination of GPS and GLONASS significantly reduces the PDOP value. As a result, the positioning errors are decreased considerably in contrast to those achieved from only one satellite system. Table 2 provides the RMS statistical results based on the positioning errors starting from 1300th epoch when the position filter first meets the pre-defined convergence criterion. The positioning solutions for the combined case have RMS values of 0·322, 0·096 and 0·342 m in the East, North and Up directions, which are significantly smaller than GPS-only PPP whose RMS values are 0·551, 0·188 and 0·511 m, respectively. The positioning accuracy for GLONASS-only PPP is apparently worse than GPS-only PPP because of the smaller number of satellites in the kinematic PPP processing.

Figure 5. Kinematic positioning errors with respect to differential solutions for single-frequency PPP using GPS-only, GLONASS-only and combined GPS/GLONASS observations.

Figure 6. PDOP and number of satellites used in the GPS-only, GLONASS-only and combined GPS/GLONASS single-frequency PPP.
Table 2. RMS statistics of kinematic positioning errors (m).

5. GGSF PPP SOLUTION ASSESSMENT USING GLOBAL IGS DATA
The performance of the GGSF PPP was assessed using datasets collected on 1 June 2012 from 22 IGS stations, which are globally distributed as shown in Figure 7. All observations had a sampling rate of 30 s. The positioning accuracy and convergence time for GGSF PPP are compared to GPS-only and GLONASS-only single-frequency PPP. For each station, three sessions of datasets were processed and each session had a time length of 3 hours. Three hours of data are normally sufficient to ensure that the float ambiguities are resolved. The IAC final precise orbit products and 30 s satellite clock corrections were used to correct satellite orbit and clock errors. The elevation mask angle and Kalman filter settings are the same as those used in the previous static processing.

Figure 7. Geographical distribution of the 22 IGS stations used for single-frequency PPP processing.
Figure 8 shows the positioning errors for GPS-only, GLONASS-only and combined GPS/GLONASS PPP processing from all three sessions at 6 of the 22 stations. The six stations are distributed at high, middle and low latitude regions. Thus their positioning solutions represent the single-frequency PPP results for these latitude regions. It can be clearly seen how the position filter converges in East, North and Up directions. In most cases, the GGSF solutions can converge to stable values more quickly and get positioning errors smaller than the GPS-only or GLONASS-only PPP results during the entire session.

Figure 8. Positioning errors for GPS-only, GLONASS-only and combined GPS/GLONASS single-frequency PPP using observations on 1 June 2012. The IGS datasets are collected from: high latitude stations (a) BAKE and (b) TIXI; mid-latitude stations (c) MAS1 and (d) BRMU; low latitude stations (e) BAKO and (f) MAL2.
In order to assess the positioning accuracy, the positioning errors at the last epoch of each session for all 22 stations are plotted in Figure 9. Figure 9 clearly illustrates the GGSF PPP has better accuracies than the GPS-only or GLONASS-only single-frequency PPP.

Figure 9. Distributions of positioning errors for GPS-only, GLONASS-only and combined GPS/GLONASS single-frequency PPP processing using three-session datasets collected at 22 IGS stations. The distributions in the East, North and Up components are displayed in the top, middle and bottom panels, respectively.
The convergence criterion is the same as that defined in previous section (i.e. smaller than 0·15 m in the East and North directions and 0·3 m in the vertical direction). Figure 10 depicts the distribution of the convergence time in units of minutes, i.e. the period from the first epoch of PPP to the convergence epoch, for all sessions in the East, North and Up directions. The improvement of GGSF PPP on the convergence time is significant for all three components. The percentage bars at the 180th minute indicate that the position filter does not converge during the entire 3-hour data session.

Figure 10. Distributions of convergence time for GPS-only, GLONASS-only and combined GPS/GLONASS single-frequency PPP processing using three-session datasets collected at 22 IGS stations. The distributions in the East, North and Up components are displayed in the top, middle and bottom panels, respectively.
Table 3 presents the statistical results for the positioning error and convergence time in three components. The three-dimensional positioning accuracy for GGSF PPP has an improvement of 31% and 28% over the GPS-only and GLONASS-only PPP results, respectively. In terms of convergence time, it is 71 min for GGSF PPP in the East component, shorter than 105 min in the GPS-only and 103 min in the GLONASS-only cases. In the North component, it is 33 min, shorter than 48 min and 53 min for GPS-only and GLONASS-only, respectively. In the Up component, the GGSF PPP needs 59 min to converge, but it takes 79 min and 75 min for GPS-only and GLONASS-only PPP, respectively, to converge. The improvement of the GGSF PPP on the convergence time is 32%, 31% and 25% over GPS-only and 31%, 38% and 21% over GLONASS-only in East, North and Up coordinate components, respectively. Apparently, the GGSF PPP has improved the positioning accuracy and shortened the convergence time significantly.
Table 3. RMS statistics of positioning errors and convergence time for GPS-only, GLONASS-only and combined GPS/GLONASS single-frequency PPP.

It should be noticed in Table 3 that the statistical results for GLONASS-only PPP are comparable with GPS-only PPP in both positioning accuracy and convergence time, though the number of tracked GLONASS satellites is significantly fewer than GPS, as shown in Figure 11. Figure 11 displays the average number of satellites and PDOP for each session. The smaller number of GLONASS satellites sometimes results in significantly large PDOP values. Furthermore, note that in the computation of average GLONASS-only PDOP, PDOP values larger than 30 have been excluded. The test results clearly indicate that the positoning accuracy and convergence time of GGSF PPP can be improved over GPS-only and GLONASS-only PPP results because of the benefit from an increased number of satellites and improved satellite geometry.
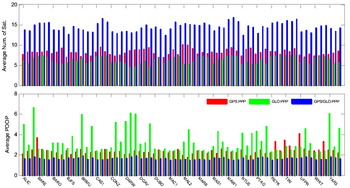
Figure 11. Average number of satellites and PDOP at 22 IGS stations for GPS-only, GLONASS-only and combined GPS/GLONASS single-frequency PPP processing. Each station includes 3 sessions of datasets.
6. CONCLUSIONS
A combined GPS/GLONASS Single-Frequency (GGSF) Precise Point Positioning (PPP) approach is proposed to improve the performance of GPS-only PPP by increasing the positioning accuracy and shortening the convergence time. The GGSF PPP position convergence criterion is defined as East and North errors of less than 15 cm and a vertical error of less than 30 cm. Different types of precise orbit and clock products from the Information – Analytical Centre, Russia (IAC) and the European Space Operations Centre, Germany (ESA/ESOC) are used to analyse the positioning accuracy. The results indicate that using rapid and ultra-rapid products degrades GGSF PPP position accuracy by a few centimetres in comparison to the use of final products. When comparing the GGSF PPP to the dual-frequency PPP, the former needs 112 min to converge in static positioning while the latter needs only 10 min. After convergence, the GGSF PPP achieves a horizontal accuracy similar to dual-frequency PPP and a slightly degraded vertical accuracy. The GGSF PPP was extensively assessed using static data collected from 22 global IGS stations. RMS statistical results indicate that the static GGSF PPP can reach an accuracy of 0·057, 0·028 and 0·121 m in East, North and Up directions, respectively. The position filter typically converges at 71, 33 and 59 min in the East, North and Up directions, respectively. Both positioning accuracy and convergence time have been improved by approximately 30% in comparison with the results from GPS-only, or GLONASS-only, single-frequency PPP. A kinematic GGSF PPP test was conducted. The kinematic results illustrate even more significant benefits from the combined GPS and GLONASS signals. Further improvement can be expected when more GLONASS satellites are available.
ACKNOWLEDGEMENTS
The financial support from National Natural Science Foundation of China (No: 41004011) is greatly appreciated. The second author is grateful for receiving support from the Hong Kong Polytechnic University projects 1-ZV6L, A-PJ63 and A-PJ78. The second author is also thankful for the support given by the Programme of Introducing Talents of Discipline to Universities (Wuhan University, GNSS Research Centre), China. The International GNSS Service is acknowledged for providing the data used in this study.













