Preprint
Review
Exploring ChatGPT Capabilities and Limitations: A Critical Review of the NLP Game Changer
Altmetrics
Downloads
4144
Views
2897
Comments
0
This version is not peer-reviewed
Advances in Artificial Neural Networks
Artificial Intelligence (AI) and Machine Learning
Submitted:
23 March 2023
Posted:
27 March 2023
You are already at the latest version
Alerts
Abstract
ChatGPT, a groundbreaking natural language processing technology released just three months ago, has attracted significant attention due to its remarkable capabilities. This AI milestone has urged researchers, industry, decision-makers, and governments to examine this technology, including its implications, threats, and benefits. Despite the short period since its release, several researchers have examined ChatGPT from different perspectives. This paper presents a comprehensive review of ChatGPT, highlighting its technical novelties compared to previous models and analyzing existing research from various perspectives. We followed a rigorous methodology to conduct a critical review of existing research on ChatGPT and developed a taxonomy for the different areas of study. Additionally, we identify future challenges and research trends associated with ChatGPT. Our paper is the first critical review of ChatGPT literature, providing valuable insights for practitioners and policymakers. This paper serves as a reference for researchers seeking to advance research on ChatGPT, including its applications and development.
Keywords:
Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning
1. Introduction
Natural Language Processing (NLP) has been a rapidly growing field for several years, but the release of ChatGPT (Chat Generative Pre-trained Transformer) in November 2022 sparked a surge of interest and excitement in the technology. ChatGPT, which is a large language model trained by OpenAI, demonstrated impressive capabilities in understanding and generating human-like language. Its ability to answer questions, carry out conversations, and generate coherent and contextually appropriate responses was a significant leap forward in the development of conversational AI.
Figure 1 illustrates the exponential rise in popularity of ChatGPT since its initial release, showcasing its dominance over other widespread technologies such as Transformers, NLP, and Computer Vision. The data was extracted from a web-based media analytics tool and covers the trends over the last three months. As evident from the graph, ChatGPT has surpassed other technologies by a considerable margin in terms of interest and mentions. Interestingly, we can also observe a spike in the popularity of Transformers technology, which seems to be synchronized with the release of ChatGPT. Nonetheless, ChatGPT continues to remain the frontrunner in the field of natural language processing, and its popularity only seems to be on the rise.
The popularity of ChatGPT has renewed the interest in NLP research, with many companies and organizations investing in developing similar language models or using its capabilities. The availability of large pre-trained language models, such as GPT-3, has also made it easier for researchers and developers to build sophisticated NLP applications without the need for extensive data training.
1.1. Why ChatGPT Became Popular?
ChatGPT is, in the end, a sophisticated chatbot, and the chatbot concept is not new as it has been developed since the early release of LSTMs and has been extensively used in several applications such as automated customer service support [1], E-Commerce [2], Healthcare [3], and Education [4]. However, while these chatbots offer decent business services, they suffer from several limitations, which we summarize in three main shortcomings:
- Limited context awareness: typical chatbot systems are trained on a limited context that serves the business requirements, such as customer service or e-commerce. This can limit their understanding capabilities and result in unsatisfying interactions for users. Furthermore, within the same context, these chatbots may struggle to address user queries if the intent is unclear enough to the engine due to limited pre-programmed rules and responses. This usually leads to unsatisfying interactions with users’ experience. However, ChatGPT has demonstrated superior performance compared to existing chatbots in its ability to understand broad contexts in natural language conversations. Its advanced language model allows it to analyze and interpret the meaning behind user queries, leading to more accurate and satisfying responses.
- Limited scale: Another limitation of traditional chatbot systems is their limited scale. These systems are typically trained on a relatively small amount of data related to the context of operation due to the high cost of data labeling and training for large data sizes. In contrast, ChatGPT has overcome these barriers by being trained on a massive amount of data from the internet, with a size of 570GB. This large-scale language model used in ChatGPT allows it to generate human-like responses that can mimic the tone, style, and humor of a human conversation. Traditional chatbots often provide robotic and impersonal responses, which can lead to unsatisfactory interactions with users. However, ChatGPT’s advanced language model and large-scale training allow it to generate more natural and engaging responses.
- Limited text generation ability: Traditional chatbot systems often lack the flexibility and adaptability required to handle complex and dynamic natural language understanding and generation. They often rely on pre-written intents, responses, or templates, leading to repetitive, predictable, or irrelevant answers that fail to engage users or meet their needs. Moreover, they struggle to generalize to new, unseen data, limiting their usefulness in real-world scenarios where the topics and contexts can vary widely. In contrast, ChatGPT leverages a powerful transformer architecture and a massive amount of training data to generate high-quality and diverse text outputs that closely resemble human language. By learning patterns and relationships between words and phrases from various sources, ChatGPT can capture the nuances and subtleties of different domains and produce relevant and coherent responses even to open-ended or ambiguous queries.
With the growing interest in ChatGPT, this paper aims to provide a comprehensive review of the language model, shedding light on its technical novelty and the reasons why it has become a hot topic in the field of information technology. Additionally, we survey recent research papers published since ChatGPT’s release, categorize them, and discuss their contributions to the assessment and development of the ChatGPT language model. Finally, we suggest some potential areas of future research that could be explored in relation to ChatGPT.
1.2. Related Surveys
Only a few survey articles related to ChatGPT and its application are available in the literature. In this subsection, we summarize the main contributions of the most relevant surveys.
The survey [5] explored the historical evolution and technology of ChatGPT, highlighting its potential applications in various domains, including healthcare, education, and research. The article also addressed some significant limitations and ethical concerns surrounding ChatGPT. One of the unique aspects of the article is the authors’ attempt to engage ChatGPT in a conversation and obtain its perspective on the questions posed by the authors. Finally, the article provided insights into the capabilities, limitations, and future directions of ChatGPT technology. Lecler et al. [6] reviewed the current applications of GPT models in radiology, including image classification, segmentation, analysis, and natural language processing for radiology reports. The authors also discussed the future possibilities of using GPT models, such as in personalized medicine and improving radiology education.
Omar et al. [7] compared the effectiveness of ChatGPT and traditional question-answering methods for knowledge graphs and discussed potential future directions for developing knowledge graph chatbots in their survey. First, an overview of knowledge graphs and their applications and the current state of question-answering systems is presented. Then, the authors compared the performance of ChatGPT and traditional question-answering methods on a benchmark dataset of knowledge graph questions. The results demonstrated that ChatGPT outperformed traditional methods regarding the accuracy and naturalness of responses. Haleem et al. [8] presented an overview of ChatGPT and its importance. Moreover, various progressive workflow processes of the ChatGPT tool are illustrated with diagrams. This survey further examined the specific features and capabilities of ChatGPT as a support tool and explored its significant roles in the current scenarios.
The distribution of currently published articles through various publishers is presented in bar graphs of Figure 2 and Figure 3. It demonstrates that limited literature is available on ChatGPT, and there is still room for improvements and contributions for upcoming researchers in this emerging research area.
1.3. Contributions and Research-Structure
The contributions of this survey are summarized in the following key points
- We provide an in-depth analysis of the technical advancements and innovations that distinguish ChatGPT from its predecessors, including generative models and chatbot systems. This analysis elucidates the underlying mechanisms contributing to ChatGPT’s enhanced performance and capabilities.
- We develop a comprehensive taxonomy of recent ChatGPT research, classifying studies based on their application domains. This classification enables a thorough examination of the contributions and limitations present in the current literature. Additionally, we conduct a comparative evaluation of emerging ChatGPT alternatives, highlighting their competitive advantages and drawbacks.
- We identify and discuss the limitations and challenges associated with ChatGPT, delving into potential areas of improvement and unexplored research opportunities. This discussion paves the way for future advancements in the field, guiding researchers and practitioners in addressing the current gaps in ChatGPT research and applications.
This paper is structured as follows: Section 2 delves into ChatGPT’s background and technological innovations, such as the fusion of transformers and reinforcement learning with human feedback. Section 3 examines ChatGPT competitors and their comparative analysis. Section 4 highlights emerging ChatGPT applications and research by summarizing pertinent studies. Section 5 outlines challenges and future directions, and Section 6 concludes the paper.
2. Background and Main Concepts
2.1. GPT-3 Model: Leveraging Transformers
The release of the GPT-3 model family by OpenAI has set the bar very high for its direct competitors, namely Google and Facebook. It has been a major milestone in developing natural language processing (NLP) models. The largest GPT-3 configuration comprises 175 billion parameters, including 96 attention layers and a batch size of 3.2 million training samples. GPT-3 was trained using 300 billion tokens (usually sub-words) [9].
The training process of GPT-3 builds on the successful strategies used in its predecessor, GPT-2. These strategies include modified initialization, pre-normalization, and reverse tokenization. However, GPT-3 also introduces a new refinement based on alternating dense and sparse attention patterns [9].
GPT-3 is designed as an autoregressive framework that can achieve task-agnostic goals using a few-shot learning paradigm [9]. The model can adapt to various tasks with minimal training data, making it a versatile and powerful tool for NLP applications.
To cater to different scenarios and computational resources, OpenAI has produced GPT-3 in various configurations. Table II-A5 summarizes these configurations, which range from a relatively small 125 million parameter model to the largest 175 billion parameter model. This allows users to choose a model that best fits their needs and resources.
All GPT (Generative Pre-trained Transformer) models, including the most recent GPT-3 model, are built based on the core technology of Transformers. The Transformer architecture was first introduced in the seminal paper "Attention is All You Need" by Vaswani et al. in 2017 [10], which has significantly impacted the deep learning research community, starting with sequential models and extending to computer vision. In the next sub-section, we provide a detailed overview of the Transformer technology and how it was leveraged in GPT-3 for text generation.
2.1.1. Transformers as Core Technology
Transformers refer to the revolutionary core technology behind ChatGPT. Transformers have transformed how sequence-to-sequence models are processed, significantly outperforming traditional models based on recurrent neural networks. Although Transformers are based on classical encoder-decoder architecture, it dramatically differs in integrating the concept of self-attention modules, which excels in capturing long-term dependencies between the elements (i.e., tokens) of the input sequence. It leverages this information to determine each element’s importance in the input sequence efficiently. The importance of each element is determined through the self-attention mechanism, which computes a weight for each element based on its relevance to other tokens in the sequence. This enables Transformers to handle variable-length sequences better and capture complex relationships between the sequence elements, improving performance on various natural language processing tasks. Another critical feature is positional embedding that helps transformers learn the positional information of tokens within the sequence. It allows differentiating between tokens with the same contents but at different positions, which provides better context representation that improves the models’ accuracy. These features represent a significant strength in ChatGPT for providing accurate natural language generation, as compared to its peer, particularly with being trained on large datasets of 570 GB of Internet data.
In general, a transformer comprises three featured modules: (i.) Encoder-Decoder module, (ii.) Self-Attention module, (iii.) Positional Embedding module.
In the following sub-section, we will present the core functionalities of these modules.
2.1.2. Encoder-Decoder Architecture
When Transformers architecture was first designed in [10] as shown in Figure 4, they were applied in machine translation, where an input sequence of an initial language is transformed to the output sequence of the target language. The Transformer architecture followed an encoder-decoder model, where the encoders map a discrete representation of the input sequence (i.e., words, characters, sub-words) to a continuous representation denoted as an embedding vector (i.e., a vector of continuous values). The decoder takes embeddings as input and generates an output sequence of elements one at a time. As the transformer is an autoregressive generative model, it predicts the probability distribution of the next element in the output sequence, given the previous sequence, which can be seen as a special case of Hidden Markov Chains (HMMs). However, HMMs do not have the ability to capture long-term dependencies bidirectionally as transformers do.
Unlike other models that use both an encoder and a decoder or an encoder only, like the Bert model family from Google [11], ChatGPT relies only on pure decoder architecture, illustrated in Figure 5, as defined in the first GPT paper [12]. Specifically, the underlying GPT model applies unidirectional attention using a language masking strategy to process the input sequences token-wise. The decoder is trained to take the first token of the input sequence as a start token and then generate subsequent output tokens based on the input sequence and previously generated tokens. This architecture represents the standard model for language modeling with the objective of generating the sequence of tokens with the highest likelihood given a context (i.e., input sequence and previously generated tokens). The reason why ChatGPT architecture does not rely on an encoder is that the GPT models are trained on a large corpus of textual datasets, using unsupervised learning, to predict the next sequence of words, given a context. Therefore, these models are trained to generate text rather than mapping an input to an output, as in a typical encoder-decoder architecture. As such, the text embedding is directly fed into the self-attention modules to learn the complex relationship between these models in a cascade of self-attention layers. The self-attention module is what makes transformers a powerful tool, which will be explained further in the next section.
2.1.3. Self-Attention Module
Self-attention stands as the core module that empowers transformers to achieve their remarkable performance. They have the ability to capture complex dependencies between the tokens in an input sequence and efficiently determine the weight of each token in an input sequence, in addition to their relative importance. While the self-attention concept may look complex, it relies on the notion of semantic similarity between vectors (in our case, token embeddings) using the dot product. The dot product of two vectors determines the cosine distance between the two vectors, considering their amplitude and the relative angle. The higher the dot product between two embeddings, the more semantically similar they are, indicating their importance in the overall context of the input sequence.
Self-Attention in transformers also relies on the Query (Q), Key (K), and Value (V) concepts. This concept is not new and is borrowed from the Information Retrieval literature and, more specifically, from query processing and retrieval, such as in search engines. In Information Retrieval, a query is a set of tokens used to search for relevant documents from a collection of stored documents. A document’s relevance score is calculated based on the similarity between the query and the document. The similarity score is determined by comparing the query tokens to the documents tokens (i.e., keys) and their corresponding weights (i.e., values). The dot product measures the cosine similarity between these vectors and calculates the relevance scores. This is what exactly happens in the self-attention modules of transformers illustrated in Figure 6.
In transformers, an input sequence is converted into a set of three vectors, namely, the query, the key, and the value vectors. Consider a sentence with a sequence of tokens (i.e., words, sub-words, or characters).
- The Query (Q): This vector represents a single token (e.g., word embedding) in the input sequence. This token is used as a query to measure its similarity to all other tokens in the input sequences, equivalent to a document in an information retrieval context.
- The Key (K):This vector represents all other tokens in the input sequence apart from the query token. The key vectors are used to measure the similarity to the query vector.
- The Value (V): This vector represents all tokens in the input sequence. The value vectors are used to compute the weighted sum of the elements in the sequence, where the weights are determined by the attention weights computed from the query and key vectors through a dot-product.
In summary, The dot product between the query vectors and the key vectors results in the attention weights, also known as the similarity score. This similarity score is then used to compute attention weights determining how much each value vector contributes to the final output.
Formally, the self-attention module is expressed as follows:
Where , , and are the packed matrix representations of queries, keys, and values, respectively. N and M denote the lengths of queries and keys (or values), while and denote the dimensions of keys (or queries) and values, respectively. The dot-products of queries and keys are divided by to alleviate the softmax function’s gradient vanishing problem, control the magnitude of the dot products, and improve generalization. This is known as a scaled dot product. The result of the attention mechanism is given by the matrix multiplication of A and V. A is often called the attention matrix, and softmax is applied row-wise.
In some cases, a mask could be applied relevance score matrix (query to key dot product) to consider specific dependency patterns between the tokens. For example, in text generation, like ChatGPT, the self-attention module uses a mask that returns the lower triangular part of a tensor input, with the elements below the diagonal filled with zeros. This helps capture the dependency of a token with all previous tokens and not with future ones, which is the partner needed in text generation.
The algorithm of a self-attention module (with mask) is presented in Algorithm 1.
| Algorithm 1: Self-Attention Module with Mask |
|
Require: Q, K, and V matrices of dimensions , , and , respectively Ensure: Z matrix of dimension Step 1: Compute the scaled dot product of Q and K matrices: Step 2: Apply the mask to the computed attention scores (if applicable): if mask is not None then {Element-wise multiplication} end if Step 3: Compute the weighted sum of V matrix using A matrix as weights: Step 4: Return the final output matrix Z. |
Note that the algorithm takes in matrices Q, K, and V, which are the query, key, and value matrices, respectively, and returns the output matrix Z. The softmax function is applied row-wise to the scaled dot product of Q and K matrices, which are divided by the square root of the key dimension . The mask is applied in Step 2 before computing the weighted sum in Step 3. The element-wise multiplication of the mask and attention scores sets the attention scores corresponding to masked tokens to zero, ensuring that the model does not attend to those positions. The resulting matrix A is used as weights to compute the weighted sum of V matrix, resulting in the output matrix Z.
2.1.4. Multi-Head Attention
Traditional NLP tasks, particularly ChatGPT, deal with vast and complex data. Therefore, using only one attention head may not be sufficient for capturing all relevant information in a sequence. Multi-head Attention allows for parallel processing since the self-attention operation is applied across multiple heads. This can result in faster training and inference times than a single-head self-attention mechanism.
Multi-Head Attention also captures multiple between the query and the key-value pairs in the input sequence, which enables the model to learn complex patterns and dependencies in the data. It also helps increase the model’s capacity to learn advanced relationships over large data.
Formally, the multi-head attention function can be represented as follows:
where , and , , , and .
2.1.5. Positional Embedding
If only the data without its order is considered, then the self-attention mechanism used in transformers becomes permutation invariant, which processes all tokens equally without considering their positional information. This may result in the loss of important semantic information as the importance of each token with respect to other tokens in the sequence is not captured. Therefore, it is necessary to leverage position information to capture the order and importance of tokens in the sequence.
To address the issue of losing important position information, the transformer model creates an encoding for each position in the sequence and adds it to the token before passing it through the self-attention and feedforward layers. This allows the model to capture the importance of each token concerning others, considering its position in the sequence.
In the transformer architecture of ChatGPT, the positional embedding is added to the input embeddings at the entrance of the decoder. The positional embedding is expressed as follows.
Given a sequence of inputs , the position embedding matrix is calculated as:
This equation calculates the value of the position embedding at position i, given the maximum sequence length d and the embedding size k. The value of k determines whether the sin or cos function is used, and is typically set to an even number in transformer models.
| Model Name | No. of Params | No. of Layers | Embedding Size | No. of Heads | Head Size | Batch Size | Learning Rate |
| GPT3-Small | 125M | 12 | 768 | 12 | 64 | 0.5M | 6.0 × 10−4 |
| GPT3-Medium | 350M | 24 | 1024 | 16 | 64 | 0.5M | 3.0 × 10−4 |
| GPT3-Large | 760M | 24 | 1536 | 16 | 96 | 0.5M | 2.5 × 10−4 |
| GPT3-XL | 1.3M | 24 | 2048 | 24 | 128 | 1M | 2.0 × 10−4 |
| GPT3-2.7B | 2.7B | 32 | 2560 | 32 | 80 | 1M | 1.6 × 10−4 |
| GPT3-6.7B | 6.7B | 32 | 4096 | 32 | 128 | 2M | 1.2 × 10−4 |
| GPT3-13B | 13B | 40 | 5140 | 40 | 128 | 2M | 1.0 × 10−4 |
| GPT3-175B | 175B | 96 | 12288 | 96 | 128 | 3M | 0.6 × 10−4 |
2.2. From GPT3 to InstructGPT: : Leveraging Reinforcement Learning
As an attempt to align its GPT3-based chatbot to human intentions, OpenAI performed a significant and innovative overhaul of the GPT-3 model, including state-of-the-art, supervised fine-tuning (SFT) and reinforcement learning from human feedback (RLHF) [13] algorithms. Their effort resulted in the instructGPT model [14], which has laid the foundations for the groundbreaking ChatGPT platform [15].
2.2.1. Reinforcement Learning from Human Feedback (RLHF)
Advanced reinforcement learning (RL) models interact with complex real-world environments to achieve pre-defined goals. In most instances, these models learn independently by continuous feedback from their environments on their recent actions/decisions. However, this learning process can be time-consuming and expensive computationally. In their seminal work, Christiano and his team from DeepMind showed that expressing the goals of the RL models using human preferences can significantly improve the learning experience in such complex environments where access to the reward functions is not possible [13]. Aside from resolving the lack of access to the reward function, the RL solution, proposed by Christiano et al., requires human intervention in less than 1% of the time the RL model interacted with its environment. Such small human intervention allows tackling problems related to real-world environments with higher complexities, including Atari games and simulated robot locomotion. To estimate the rewards collected from the environment, a non-linear reward estimation function is proposed as a trainable deep neural network. This network is augmented with "natural" preferences based on sporadic human intervention ( of the learning time). Given the non-stationarity of the adopted reward function, Christiano et al. relied on policy gradient methods [16] to extract the best policy for the RL model following the successful work of Ho and Ermon [17]. The RL models representing the simulated robot locomotion and Atari games are solved using the trust region policy optimization (TRPO) and advantage actor-critic (A2C) algorithms, respectively [18,19]. Ouyang et al. devised a fine-tuning strategy for the OpenAI largest model, GPT3-175B [9], based on the PPO algorithm and a learnable reward function that takes into account human preferences [14]. Human preferences are centered on three main goals: helpfulness, harmlessness, and honesty (HHH). The fine-tuned model, called instructGPT, did not only meet the human preferences to a large extent, but the resulting model size was impressively smaller than its parent model. More specifically, the instructGPT model consisted of 1.3 billion parameters which make it comparable to lightweight GPT-3 versions such as GPT3-XL and GPT3-2.7B.
Figure 7 illustrates the basic configuration of RL models. In most of these models, the RL agent interacts with its surrounding environment by taking specific actions and collecting some rewards (could be negative depending on the action taken). The possible actions and rewards are usually defined using a Markov decision process (MDP). MDP-based RL models are described using the following tuple [16]:
- : Set of states where each state, , "encodes" the environment (i.e., the user prompts and agent completions).
- : Set of actions that the dialogue agent can take at any step t by generating a new prompt completion.
- : Transition probabilities when taking action at state to reach state .
- : Reward achieved when taking action to transition from to . When fine-tuning dialogue agents, it is a common practice to assume the rewards independent of the actions.
- : Discount (or forgetting) factor set to a positive number smaller than 1. For simplicity, can be fixed to a typical value such as ..
In the LRHF settings, the cardinality of the state space, , and action set, , have reasonable sizes, which ensures tractable policy solutions [14].
To account for the uncertainties in the user-agent dialogue interaction, the reward function is formulated using the expectation operator:
where denotes the expectation operator. The infinite sum in Equation (1) will always converge as is smaller than one by design. Therefore, Equation (1) allows handling continuous user/agent interactions since the sum in Equation (1) will always converge [16].
Once the reward function is defined, the value function of a state is expressed as the expected cumulative reward accumulated by taking action at this state and acting "optimally" till the end of the dialogue session [16]:
2.2.2. State-of-the-Art Related to RLHF-Based Dialogue Systems
Over the last few years, three main players have emerged in the field of RLHF-based dialogue systems, including OpenAI [14], Deepmind [22], and Anthropic [23]. In their attempt to teach dialogue systems to summarize texts, the OpenAI team [24] reported one of the earliest success stories in LRHF adoption in the field of natural language processing (NLP). In this work, varying-size sentences are summarized considering human preferences in terms of summary accuracy, coverage, and coherence [24]. Figure 8 depicts the main differences between AI-based and human-based text summarization processes.
By treating the summarization model as an RL agent, Stiennon et al. [24] devised a strategy consisting of policy training guided by the outputs of the reward model as shown in Figure 9. The LM policy is trained on a variant of the PPO algorithm that has undergone several hyperparameter tuning [24]. As it is impossible to have a human labeler intervene at each training episode, Stiennon et al. suggested using a transformer-based model to mimic the human scoring rationale to rate the summarizations produced by the pre-trained and fine-tuned models. As reported in [24], the reward module consists of a transformer model with six layers and eight attention heads. The model produces embedding vectors of 512. The training approach used to train the reward module is illustrated in Figure 10.
The loss function of the reward module, parameterized with , is defined as follows [14]:
Where and represent the outputs of the reward module the input text, preferred and less-preferred summarizations by the human labeler, respectively. The set of summarizations labeled by a human is denoted by D. It is worth noting that the OpenAI team has treated each possible comparison as a separate training sample that will contribute to different gradient updates [14].
3. ChatGPT Competitors
ChatGPT is one of the most advanced natural language processing models available today. However, several other language models are considered competitors to ChatGPT, each with unique strengths and weaknesses. These models have been developed by some of the world’s most prominent tech companies and research institutions. They are designed to tackle various language-based tasks, including machine translation, language generation, education, and industry. This review will focus on the most well-known ChatGPT competitors, including Google Bard, Chatsonic, Jasper Chat, OpenAI Playground, Caktus AI, Replika, Chai AI, Neeva AI, Rytr, and PepperType.
3.1. Google Bard
Google Bard is a recently introduced chatbot technology that emerged due to the growing competition in AI, exemplified by counterparts such as ChatGPT. Its primary objective is to emulate a genuine conversation with a human user. It utilizes natural language processing and machine learning algorithms to furnish accurate and practical answers to various inquiries [25]. These tools can be highly beneficial for smaller businesses that aim to provide natural language assistance to their customers but need more resources to hire a large support team or rely on Google’s search tools. In addition, Bard can seamlessly integrate into various digital systems, including websites, messaging platforms, and desktop and mobile applications, to enhance customer experience [25].
3.2. Chatsonic
ChatSonic is a highly potent conversational AI chatbot designed to overcome the constraints of ChatGPT by OpenAI. This advanced AI chatbot is based on the latest GPT-3.5 model. It utilizes cutting-edge Natural Language Processing (NLP) and Machine Learning (ML) technologies to automate the text and image generation process [26]. ChatSonic can provide accurate information by utilizing internet results to generate responses, which significantly reduces the possibility of errors. Additionally, this AI chatbot can remember previous conversations and build upon them, ensuring a seamless dialogue flow [26]. Furthermore, ChatSonic offers 16 distinct personas, allowing users to engage with different virtual personalities, ranging from an accountant to a poet.
3.3. Jasper Chat
Jasper has been a prominent player in the AI content generation industry and has garnered considerable acceptance from its users. Apart from its content creation capabilities and other offerings, Jasper has recently introduced a chatbot named Jasper Chat. This alternative to ChatGPT is based on GPT 3.5 and other language models and has partnered with OpenAI [27]. However, unlike ChatGPT, which is accessible to anyone, this chatbot has been specifically developed for businesses in advertising, marketing, and more domains.
3.4. OpenAI Playground
OpenAI Playground is an intuitive web-based platform that simplifies creating and testing predictive language models. This tool is both a predictive language and writing tool, allowing users to express themselves in diverse ways [28]. This chatbot enables users to type almost anything and receive an accurate and human-like response. It employs a range of models, including all the models in the GPT-3 series and others, to inspire creativity. OpenAI GPT-3 Playground can generate text, explain concepts, summarize text, translate text, write novels, and much more [28].
3.5. Caktus AI
Caktus AI is an educational tool specifically designed for students. The first-ever artificial intelligence tool enables students to automate their homework, freeing up time for other tasks [29]. Caktus AI offers a range of features tailored to students, such as essay and paragraph writers, as well as discussion, question, and coding tools. Additionally, students can access career guidance and language assistance through custom cover letter writers, and language tutor lessons [29].
3.6. Replika
Replika is specifically designed to foster companionship and nurture relationships. Millions of people worldwide have utilized Replika as a chatting platform and a means of forming deep, personal connections [30]. Replika is equipped with the autoregressive GPT-3 language model, enabling it to acquire knowledge from its past inputs [30]. As it prioritizes meaningful conversation, it can draw from previous interactions and tailor itself to the individual user, creating a more personalized experience.
3.7. Chai AI
Chai AI is a comprehensive service that allows users to communicate with various chat AIs across the globe. The platform is designed to be highly intuitive, allowing users to easily browse and select from various bots with unique personalities [31]. Whether users seek a therapeutic or romantic encounter, Chai AI’s bots respond in real time without significant delay. Moreover, they possess a multi-turn ability, which enables them to remember past conversations and respond accordingly [31].
3.8. Neeva AI
Neeva is an AI-powered search engine that provides users with a more convenient and user-friendly approach to web searches. It allows users to search for various topics, including recipes, gift ideas, etc., and provides answers without requiring users to navigate multiple search results. Unlike traditional search engines, Neeva delivers a single, synthesized answer summarizing the most relevant sites to a query [32]. Additionally, Neeva embeds references and citations directly in the answer, making it easy for users to verify the credibility and reliability of the sources cited.
3.9. Rytr
Rytr is an AI writing tool that aims to assist users in generating high-quality content in various contexts. The platform employs a language model AI to help writers create content for ideation or practical use. Rytr offers versatility in generating content with over 40 use cases, and 20 tones [32]. The tool also supports over 30 languages and claims to produce outputs that require minimal editing, making them pitch-perfect. To enhance its functionality, Rytr includes an SEO analyzer and plugins for WordPress, as well as a Chrome extension [32].
3.10. PepperType
Peppertype is an AI-based service that generates text-based content for various applications. Its capabilities include crafting Google Ad Copy, answering Quora questions, suggesting blog topics, composing e-commerce product descriptions, writing blog introductions and conclusions, and rewriting existing content [33]. In addition, the user-friendly website allows users to browse and select the various content platforms by category. Peppertype provides comprehensive language coverage to cater to a diverse global audience, supporting more than 25 languages [33].
4. Applications of ChatGPT
This section discusses emerging applications and research works of ChatGPT by summarizing the most relevant related studies. We have classified the literature related to ChatGPT into five distinct categories based on the context of their application. These categories include (i.) Natural Language Processing, (ii.) Healthcare, (iii.) Ethics, (iv.) Education, (v.) Industry.
4.1. Natural Language Processing
ChatGPT presents significant advances in the field of natural language processing (NLP) and has the potential to revolutionize the way we interact with machines and process natural language data.
The article [34] aims to evaluate the performance of ChatGPT compared to human experts regarding dialogue quality. The authors present a comparison corpus of human and ChatGPT dialogue and use three evaluation metrics to measure the quality of dialogue. In addition, they develop a detection model to identify human and ChatGPT-generated conversations. The results of the experiments demonstrate that the performance of ChatGPT is close to that of human experts. However, this article lacks depth and breadth in evaluating ChatGPT’s performance. The authors focus on a limited set of metrics without considering other important aspects such as accuracy, fluency, and generalizability. Furthermore, they didn’t discuss and provide concrete solutions to the issues of scalability and customization of the model. Bang et al. [35] analyzed the performance of the ChatGPT multipurpose language and dialogue model across three tasks: reasoning, hallucination, and interactivity. The experimental outcomes showed that ChatGPT performs well in all three tasks, significantly improving reasoning and interactivity in a multiple language and multimodal setting. The paper also provided a detailed analysis of ChatGPT performance, highlighting areas for improvement and potential applications. However, the article didn’t present enough evidence to support the proposed multitasking, multilingual and multimodal evaluation of ChatGPT. In addition, it doesn’t provide sufficient details on the training data and evaluation metrics. Muennighoff et al. [36] proposed a new method SGPT for applying decoder-only transformers to semantic search and extracting meaningful sentence embeddings from them. SGPT can produce state-of-the-art sentence embeddings that outperform previous methods on the BEIR search benchmark. The authors also introduced two settings for SGPT: Cross-Encoder vs. BiEncoder, and Symmetric vs. Asymmetric, and provided recommendations for which settings to use in different scenarios. However, the article primarily focuses on the performance of SGPT on the BEIR search benchmark, and it is unclear how well it performs on other semantic search tasks. Furthermore, the paper didn’t provide a detailed analysis of the biases and limitations of the proposed method, which could limit its applicability in certain scenarios.
Zhou et al. [37] comprehensively surveyed recent research advancements, current and future challenges, and opportunities for Pretrained Foundation Models (PFMs) in text, image, graph, and other data modalities. The authors reviewed the basic components and existing pretraining techniques in natural language processing, computer vision, and graph learning. They also discussed advanced PFMs for other data modalities and unified PFMs considering the data quality and quantity. The paper is technical and may be challenging for non-experts to understand. It also focuses on PFMs and their applications, but it may not provide sufficient insights into AI models’ general limitations and ethical implications. Qin et al. [38] provided an empirical analysis of the zero-shot learning ability of ChatGPT. The study evaluated the model’s performance on 20 popular NLP datasets covering seven representative task categories: reasoning, natural language inference, question answering (reading comprehension), dialogue, summarization, named entity recognition, and sentiment analysis. The article also compared ChatGPT’s performance with the most advanced GPT-3.5 model and reported recent work’s zero-shot, fine-tuned, or few-shot fine-tuned results. However, this article does not provide a detailed analysis of the study’s limitations. In addition, the article didn’t discuss the ethical implications of using large language models for NLP tasks. Ortega et al. [39] introduced linguistic ambiguity, its varieties, and its relevance in modern Natural Language Processing (NLP). It also performs an extensive empirical analysis of linguistic ambiguity in ChatGPT, a transformer-based language model. The paper presented the strengths and weaknesses of ChatGPT related to linguistic ambiguity and provided strategies to get the most out of the model. However, the paper is limited to an empirical analysis of ChatGPT’s performance in detecting linguistic ambiguity in English. It does not explore the potential impact of linguistic features or resource limitations on the model’s performance. Borji et al. [40] presented a comprehensive analysis of ChatGPT’s failures in 11 categories, including reasoning, factual errors, math, coding, and bias, along with the limitations, risks, and societal implications of large language models. The paper aims to provide a reference point for evaluating the progress of chatbots like ChatGPT over time and to assist researchers and developers in enhancing future language models and chatbots. However, it lacks an in-depth analysis of the problems associated with ChatGPT. It does not address the underlying issues that cause the failures or provide any recommendations for improving the system.
This article [41] explored the performance of ChatGPT on aspect-based and query-based text summarization tasks. The study evaluated ChatGPT’s performance on four benchmark datasets, encompassing various summaries from Reddit posts, news articles, dialogue meetings, and stories. The authors reported that ChatGPT’s performance is comparable to traditional fine-tuning methods regarding Rouge scores. However, the study relies solely on Rouge scores to evaluate the performance of ChatGPT, which may not be a sufficient indicator of summarization quality. The authors acknowledged this limitation and planned to conduct human evaluations shortly. Jiao et al. [42] provided a preliminary study on the performance of ChatGPT for machine translation tasks, including translation prompt, multilingual translation, and translation robustness. The authors explored the effectiveness of different prompts, evaluated the performance of ChatGPT on different language pairs, and investigated its translation robustness. In addition, the authors proposed an interesting strategy named pivot prompting that significantly improves translation performance for distant languages. However, the study results may not be fully reliable due to the randomness in the evaluation process. The paper also does not provide a detailed analysis of the factors affecting the translation performance of ChatGPT. Kocon et al. [43] evaluated the capabilities of the ChatGPT on 25 diverse analytical NLP tasks, most of which are subjective in nature, including sentiment analysis, emotion recognition, offensiveness and stance detection, natural language inference, word sense disambiguation, linguistic acceptability, and question answering. The authors automated ChatGPT’s querying process and analyzed more than 38k responses, comparing its results with state-of-the-art solutions. However, the study does not directly compare ChatGPT’s performance with other chatbot models. The authors also acknowledge ChatGPT’s biases but didn’t provide a detailed analysis of these biases. Additionally, the study’s focus on analytical NLP tasks may not fully reflect ChatGPT’s performance in more practical settings, such as chatbot interactions.
The aforementioned discussion related to the applications of ChatGPT in NLP is summarized in Table 2.
Table 1.
A Comparative Analysis of ChatGPT-related Works in NLP.
| Reference | Main Contributions | Strengths | Shortcomings |
|---|---|---|---|
| [34] |
|
|
|
| [35] |
|
|
|
| [39] |
|
|
|
| [40] |
|
|
|
| [41] |
|
|
|
| [42] |
|
|
|
| [43] |
|
|
|
| [38] |
|
|
|
4.2. Healthcare
ChatGPT has the potential to revolutionize the healthcare industry by improving patient outcomes, reducing costs, and facilitating more efficient and accurate diagnosis and treatment.
Mann et al. [44] examined AI’s potential role in translational medicine. It highlighted the need for further research into personalized medicine and the potential for AI-driven data analysis to be used in clinical decision-making. Furthermore, it discussed the ethical implications of AI-enabled personalized medicine and how to best utilize advanced AI technologies while minimizing risk. However, this article failed to provide adequate information about the potential risks of using AI in medical applications. Additionally, it didn’t provide any concrete evidence or examples of successful applications of AI in medical contexts. Antaki et al. [45] conducted a study to evaluate the performance of ChatGPT in ophthalmology. The outcomes indicated that ChatGPT could provide a low-cost, accurate, personalized solution for ophthalmology consultations. Furthermore, ChatGPT can accurately detect ophthalmic diseases and create treatment plans consistent with guidelines. However, this article only evaluated the performance of ChatGPT in ophthalmology and did not consider its potential applications in other medical specialties. Additionally, it didn’t provide any concrete recommendations on the performance improvement of ChatGPT. Jeblick et al. [3] used a ChatGPT-based natural language processing system to simplify radiology reports. The study found that the system can achieve high accuracy in terms of both content understanding and grammatical correctness. Furthermore, with improved readability and less medical jargon, the system could generate easier reports for laypeople to understand. However, this study has a few shortcomings. First, the authors only used a small sample size and did not comprehensively analyze the data collected. Second, this study did not assess the accuracy of the simplified reports produced by ChatGPT. Third, it didn’t provide any information on the potential impact of this technology on medical care or patient outcomes.
The article [46] focuses on the potential of AI-assisted medical education using large language models. The authors test the performance of ChatGPT on the USMLE, a comprehensive medical board examination, and an internal medical knowledge base. The results show that ChatGPT outperforms current state-of-the-art models in both tasks. The authors concluded that large language models have great potential for use in AI-assisted medical education and could help drive personalized learning and assessment. This article has a few shortcomings. First, the sample size used in the study was small, as only seven medical students completed the study. This means that the results may not be representative of a larger population. The article does not discuss the ethical implications of using AI-assisted technology in medical education. Finally, the article provides no evidence that AI-assisted medical education is superior to traditional methods. Dahmen et al. [47] analyzed the potential of ChatGPT as an AI-based tool to assist medical research. It evaluated the opportunities and challenges that ChatGPT brings, such as its ability to streamline research by eliminating manual labor and providing real-time access to the latest data, as well as its potential to introduce bias and reduce accuracy. It also provided recommendations on how to best utilize and regulate the use of ChatGPT in medical research. However, the main shortcoming of this article is that it relies heavily on one study, which is insufficient to establish definitive conclusions about the potential of AI bot ChatGPT in medical research. Additionally, the article does not provide enough detail about the methods and results of the study, which limits the ability to draw meaningful conclusions. King et al. [48] presented a perspective on the future of artificial intelligence (AI) in medicine. It discusses the potential of AI to improve the accuracy and efficiency of medical diagnostics, reduce costs, and improve access to medical care in parts of the world without adequate healthcare infrastructure. The authors also explored the ethical considerations of using AI in medicine, such as privacy, data security, and regulatory compliance. However, the article does not provide an in-depth analysis of the ethical implications of using AI in health care or the potential risks associated with its use. Additionally, the article does not discuss how AI can be used to improve patient care or how it could be used to develop new medical treatments. Bhattacharya et al. [49] evaluated the performance of a novel deep learning and ChatGPT-based model for surgical practice. The proposed model can understand natural language inputs such as queries and generate relevant answers. The outcomes demonstrated that ChatGPT outperformed baseline models in accuracy and time spent. Additionally, the study discussed the strong potential of ChatGPT for future applications in surgical practice. However, This article lacks empirical evidence to support its claims. Additionally, the study was limited in scope as it was conducted in one hospital and did not include a control group. Furthermore, the study did not consider the long-term effects of ChatGPT on patient satisfaction or outcomes, leaving these questions unanswered.
The editorial [50] explored the potential impact of the ChatGPT language model on medical education and research. It discusses the various ways ChatGPT can be used in the medical field, including providing medical information and assistance, assisting with medical writing, and helping with medical education and clinical decision-making. However, the editorial didn’t provide new research data or empirical evidence to support its claims. Instead, it primarily relies on anecdotal evidence and expert opinions, which may not represent the wider medical community’s views. This case study in [51] explored the potential of generative AI in improving the translation of environmental health research to non-academic audiences. The study submitted five recently published environmental health papers to ChatGPT to generate summaries at different readability levels. It evaluated the quality of the generated summaries using a combination of Likert-scale, yes/no, and text to assess scientific accuracy, completeness, and readability at an 8th-grade level. However, this study is limited in scope as it only evaluates the quality of generated summaries from five recently published environmental health papers. The study acknowledges the need for continuous improvement in generative AI technology but does not provide specific recommendations for improvement. Wang et al. [33] investigated the effectiveness of using the ChatGPT model for generating Boolean queries for systematic review literature searches. The study compared ChatGPT with state-of-the-art methods for query generation and analyzed the impact of prompts on the effectiveness of the queries produced by ChatGPT. However, the model’s MeSH term handling is poor, which may impact the recall of the generated queries. In addition, the study is limited to standard test collections for systematic reviews, and the findings may not be generalizable to other domains. Kurian et al. [52] highlighted the role of ChatGPT and its potential to revolutionize communication. It also sheds light on the issue of HPV vaccination and the role of oral health care professionals in promoting it. In addition, the article suggested that training and education tools can improve healthcare providers’ willingness and ability to recommend the vaccine. However, the article doesn’t provide in-depth analysis or research on either topic and relies heavily on information provided by external sources. It also does not address potential concerns or criticisms of using AI chatbots or the HPV vaccine.
The aforementioned discussion related to the applications of ChatGPT in healthcare is summarized in Table 3
Table 2.
A Comparative Analysis of ChatGPT-related Works in Healthcare.
| Reference | Main Contributions | Strengths | Shortcomings |
|---|---|---|---|
| [45] |
|
|
|
| [3] |
|
|
|
| [46] |
|
|
|
| [51] |
|
|
|
| [53] |
|
|
|
4.3. Ethics
ChatGPT has been widely discussed in the field of ethics due to its potential impact on society.
Graf et al. [54] discussed the implications of using ChatGPT in research. It emphasized the importance of responsible research that adheres to ethical, transparent, and evidence-based standards. It also highlighted the potential to use ChatGPT for more specific and in-depth research, such as understanding the impact of implicit biases and the potential risks associated with its use. The major shortcomings of this article are a lack of discussion regarding the ethical implications of using ChatGPT in research. Additionally, it does not address the potential risks associated with ChatGPT, and there is limited discussion of the potential benefits of using the technology. Hacker et al. [55] presented a brief discussion on various issues regulating large generative AI models, such as ChatGPT. The authors explored the legal, economic, and ethical considerations of regulating the use of such models, as well as proposed a regulatory framework for the safe and responsible use of ChatGPT. Finally, they concluded that a strong regulatory framework is necessary to ensure that ChatGPT is used to benefit society and maintain public safety. However, this article didn’t consider the potential impacts of using large generative AI models on privacy, data security, data ownership, and other ethical considerations. Additionally, it didn’t provide concrete proposals or recommendations to effectively regulate large generative AI models.
Khalil et al. [56] explored the potential of using a GPT-based natural language processing (NLP) model for detecting plagiarism. The authors presented the ChatGPT model, trained on a large corpus of text to generate contextualized, paraphrased sentences. The experimental outcomes report that the model could identify plagiarism with an accuracy of 88.3% and detect previously unseen forms of plagiarism with an accuracy of 76.2%. However, the article does not offer an alternate solution to the problem of plagiarism detection. Additionally, there is not enough discussion around the ethical implications of using ChatGPT to detect plagiarism. Zhuo et al. [57] presented a comprehensive exploration and catalog of ethical issues in ChatGPT. The authors analyze the model from four perspectives: bias, reliability, robustness, and toxicity. In addition, they benchmark ChatGPT empirically on multiple datasets and identify several ethical risks that existing benchmarks cannot address. The paper also examined the implications of the findings for the AI ethics of ChatGPT and future practical design considerations for LLMs. However, the article does not provide a quantitative analysis of the identified ethical issues in ChatGPT, which may cause a more nuanced understanding of the risks posed by the model.
The aforementioned discussion related to the applications of ChatGPT in ethics is summarized in Table 4.
Table 3.
A Comparative Analysis of ChatGPT-related Works in Ethics.
| Reference | Main Contributions | Strengths | Shortcomings |
|---|---|---|---|
| [55] |
|
|
|
| [56] |
|
|
|
| [57] |
|
|
|
4.4. Education
ChatGPT has the potential to enhance the quality of education by providing personalized, student-centered learning experiences that can help improve learning outcomes and promote student success.
Frieder et al. [4] discussed the capabilities of ChatGPT in education. The authors explored three key areas: First, the ability of ChatGPT to generate mathematically valid natural language statements; second, its ability to answer mathematics-related queries; and third, its ability to solve math problems. The experimental outcomes indicate that ChatGPT outperformed other models in generating mathematically valid statements and answering math questions. However, this article is largely theoretical and does not provide empirical evidence to prove the claims. Additionally, the authors do not provide any evaluation metrics or performance results to demonstrate the effectiveness of the proposed approach. Chen et al. [58] analyzed the potential impact of ChatGPT on library reference services. The article suggested that ChatGPT could help to reduce workloads, improve response times, provide accurate and comprehensive answers, and offer a way to answer complex questions. Additionally, it argued that ChatGPT could enhance the user experience and transform library reference services. However, the article does not offer sufficient details about the potential advantages and disadvantages of using ChatGPT. Furthermore, the article does not provide any information about the actual implementation of ChatGPT in library reference services. Susnjak et al. [59] evaluated the ability of ChatGPT to perform high-level cognitive tasks and produce text indistinguishable from the human-generated text. The study shows that ChatGPT can exhibit critical thinking skills and generate highly realistic text with minimal input, making it a potential threat to the integrity of online exams. The study also discussed online exams’ challenges in maintaining academic integrity, the various strategies institutions use to mitigate the risk of academic misconduct, and the potential ethical concerns surrounding proctoring software. However, the study mainly focuses on the potential threat of ChatGPT to online exams and does not provide an in-depth analysis of other potential risks associated with online exams.
Tlili et al. [60] presented a case study of ChatGPT in the context of education. The study examined the public discourse surrounding ChatGPT, its potential impact on education, and users’ experiences in educational scenarios. It also identified various issues, including cheating, honesty and truthfulness of ChatGPT, privacy misleading, and manipulation. However, this study only examines the experiences of a small number of users in educational scenarios, and the findings may not be generalizable to other contexts. In addition, it does not provide a comprehensive analysis of the ethical implications of using ChatGPT in education, which could be an area for future research. This editorial in [61] explored the potential use of an AI chatbot, ChatGPT, in scientific writing. It highlighted the ability of ChatGPT to assist in organizing material, generating an initial draft, and proofreading. The paper discussed the limitations and ethical concerns of using ChatGPT in scientific writing, such as plagiarism and inaccuracies. However, the article does not provide empirical evidence or case studies to support its claims. The potential benefits and limitations of using ChatGPT in scientific writing are discussed theoretically, but there is no practical demonstration of how this tool can assist scientific writing. Therefore, the paper lacks practical examples that can help readers better understand the potential of ChatGPT in scientific writing. King et al. [62] briefly discussed the history and evolution of AI and chatbot technology. It explored the growing concern of plagiarism in higher education and the potential for chatbots like ChatGPT to be used for cheating. Additionally, it provides suggestions for ways college professors can design assignments to minimize potential cheating via chatbots. However, it doesn’t delve into the potential benefits of using chatbots in higher education.
The aforementioned discussion related to the applications of ChatGPT in education is summarized in Table 5.
Table 4.
A Comparative Analysis of ChatGPT-related Works in Education.
| Reference | Main Contributions | Strengths | Shortcomings |
|---|---|---|---|
| [4] |
|
|
|
| [58] |
|
|
|
| [59] |
|
|
|
| [60] |
|
|
|
4.5. Industry
ChatGPT has numerous potential applications in the industry, particularly in customer service and marketing areas. It can improve efficiency, increase customer satisfaction, and provide valuable insights to companies across various industries.
Prieto et al. [63] investigated the potential of using ChatGPT to automate the scheduling of construction projects. The data mining techniques were used to extract scheduling information from project specifications and histories. The results showed that the algorithm could accurately predict the project timeline and duration with an average accuracy of 81.3%. However, the article lacks detailed information regarding implementing the ChatGPT interface and its effects on the scheduling process, as well as the lack of reliable data to support the authors’ claims that the scheduling process is improved by incorporating ChatGPT. Graf et al. [64] discussed the applications of ChatGPT in the finance industry. First, it looked at the potential of using machine learning to facilitate the analysis of financial data, as well as its potential applications in finance. Next, it presented the "Bananarama Conjecture", which suggests that ChatGPT can provide greater insights into financial research and data analysis than conventional methods. However, the authors limit their scope to the Bananarama Conjecture, a relatively narrow field that may not capture the breadth of the finance industry. Furthermore, they didn’t provide a detailed discussion of their findings’ implications, making it difficult to draw conclusions from the research.
Gozalo et al. [65] provided a concise taxonomy of recent large generative models of artificial intelligence, their sectors of application, and their implications for industry and society. The article described how these models generate novel content and differ from predictive machine learning systems. The study also highlights the limitations of these models, such as the need for enormous datasets and the difficulty in finding data for some models. However, the paper does not provide a detailed technical explanation of the models or their architecture, making it less suitable for readers interested in generative AI’s technical aspects. Additionally, the paper does not critically analyze generative AI models’ ethical and social implications. The case study [66] examined the use of ChatGPT in a human-centered design process. The study aims to explore the various roles of fully conversational agents in the design process and understand the emergent roles these agents can play in human-AI collaboration. ChatGPT is used to simulate interviews with fictional users, generate design ideas, simulate usage scenarios, and evaluate user experience for a hypothetical design project on designing a voice assistant for the health and well-being of people working from home. However, this study is limited by its focus on a single hypothetical design project. As a result, the generalizability of the findings to other design contexts may be limited. The study also relies on subjective evaluations of ChatGPT’s performance, which may be influenced by the authors’ biases or expectations.
The aforementioned discussion related to the applications of ChatGPT in the industry is summarized in Table 6.
Table 5.
A Comparative Analysis of ChatGPT-related Works in Education.
| Reference | Main Contributions | Strengths | Shortcomings |
|---|---|---|---|
| [64] |
|
|
|
| [63] |
|
|
|
| [66] |
|
|
|
5. Challenges and Future Directions
5.1. Challenges
-
Data Privacy and Ethics: The challenge of Data Privacy and Ethics for ChatGPT is complex and multifaceted. One aspect of this challenge is related to data privacy, which involves protecting personal information collected by ChatGPT. ChatGPT relies on vast amounts of data to train its language model, which often includes sensitive user information, such as chat logs and personal details. Therefore, ensuring that user data is kept private and secure is essential to maintain user trust in the technology [67,68].Another aspect of the Data Privacy and Ethics challenge for ChatGPT is related to ethical considerations. ChatGPT has the potential to be used in various applications, including social media, online communication, and customer service. However, the technology’s capabilities also pose ethical concerns, particularly in areas such as spreading false information and manipulating individuals [69,70]. The potential for ChatGPT to be used maliciously highlights the need for ethical considerations in its development and deployment.To address these challenges, researchers and developers need to implement robust data privacy and security measures in the design and development of ChatGPT. This includes encryption, data anonymization, and access control mechanisms. Additionally, ethical considerations should be integrated into the development process, such as developing guidelines for appropriate use and ensuring technology deployment transparency. By taking these steps, the development and deployment of ChatGPT can proceed ethically and responsibly, safeguarding users’ privacy and security while promoting its positive impact.
-
Bias and Fairness: Bias and fairness are critical issues related to developing and deploying chatbot systems like ChatGPT. Bias refers to the systematic and unfair treatment of individuals or groups based on their personal characteristics, such as race, gender, or religion. In chatbots, bias can occur in several ways [71,72]. For example, biased language models can lead to biased responses that perpetuate stereotypes or discriminate against certain groups. Biased training data can also result in a chatbot system that provides inaccurate or incomplete information to users.Fairness, on the other hand, relates to treating all users equally without discrimination. Chatbots like ChatGPT must be developed and deployed in a way that promotes fairness and prevents discrimination. For instance, a chatbot must provide equal access to information or services, regardless of the user’s background or personal characteristics.To address bias and fairness concerns, developers of chatbots like ChatGPT must use unbiased training data and language models. Additionally, the chatbot system must be regularly monitored and audited to identify and address any potential biases. Fairness can be promoted by ensuring that the chatbot system provides equal access to information or services and does not discriminate against any particular group. The development and deployment of chatbots must be done with a clear understanding of the ethical considerations and a commitment to uphold principles of fairness and non-discrimination.
- Robustness and Explainability: Robustness and explainability are two critical challenges that must be addressed when deploying ChatGPT in real-world applications [7].
Robustness refers to the ability of ChatGPT to maintain high performance even when faced with unexpected inputs or perturbations. In other words, robustness ensures that the model’s predictions are reliable and consistent across different contexts. For example, if ChatGPT is used to generate responses in a chatbot, it must be robust to diverse language styles, accents, and topics to provide accurate and relevant responses.
However, achieving robustness is challenging as the model’s performance can be affected by various factors such as data quality, model architecture, training algorithms, and hyperparameters. In addition, adversarial attacks can also compromise the robustness of ChatGPT. Adversarial attacks refer to deliberately manipulating inputs to mislead the model’s predictions. Therefore, robustness is a crucial challenge that must be addressed to ensure the reliability and trustworthiness of ChatGPT.
On the other hand, explainability refers to the ability of ChatGPT to provide transparent and interpretable explanations for its predictions. Explainability is crucial for building trust and accountability, especially in critical applications such as healthcare and finance. For example, suppose ChatGPT is used to diagnose a medical condition. In that case, it must be able to provide transparent and interpretable explanations for its diagnosis to ensure that healthcare professionals and patients can understand and trust its decisions.
However, explainability is also challenging as deep learning models such as ChatGPT are often seen as black boxes, making it difficult to understand how they arrive at their decisions. Recent advances in explainable AI (XAI) have proposed techniques such as attention mechanisms and saliency maps to provide interpretable explanations for deep learning models. Therefore, explainability is a critical challenge that must be addressed to ensure the transparency and accountability of ChatGPT.
5.2. Future Directions
- Multilingual Language Processing: Multilingual Language Processing is a crucial area for future work related to ChatGPT [35]. Despite ChatGPT’s impressive performance in English language processing, its effectiveness in multilingual contexts is still an area of exploration. To address this, researchers may explore ways to develop and fine-tune ChatGPT models for different languages and domains and investigate cross-lingual transfer learning techniques to improve the generalization ability of ChatGPT. Additionally, future work in multilingual language processing for ChatGPT may focus on developing multilingual conversational agents that can communicate with users in different languages. This may involve addressing challenges such as code-switching, where users may switch between languages within a single conversation. Furthermore, research in multilingual language processing for ChatGPT may also investigate ways to improve the model’s handling of low-resource languages, which may have limited training data available.
-
Low-Resource Language Processing: One of the future works for ChatGPT is to extend its capabilities to low-resource language processing. This is particularly important as a significant portion of the world’s population speaks low-resource languages with limited amounts of labeled data for training machine learning models. Therefore, developing ChatGPT models that can effectively process low-resource languages could have significant implications for enabling communication and access to information in these communities.To achieve this goal, researchers can explore several approaches. One possible solution is to develop pretraining techniques that can learn from limited amounts of data, such as transfer learning, domain adaptation, and cross-lingual learning. Another approach is to develop new data augmentation techniques that can generate synthetic data to supplement the limited labeled data available for low-resource languages. Additionally, researchers can investigate new evaluation metrics and benchmarks that are specific to low-resource languages.Developing ChatGPT models that can effectively process low-resource languages is a crucial area of research for the future. It has the potential to enable access to information and communication for communities that have been historically marginalized due to language barriers.
- Domain-Specific Language Processing: Domain-specific language processing refers to developing and applying language models trained on text data from specific domains or industries, such as healthcare, finance, or law. ChatGPT, with its remarkable capabilities in natural language processing, has the potential to be applied to various domains and industries to improve communication, decision-making, and automation.
One potential future direction for ChatGPT is to develop domain-specific language models that can understand and generate text specific to a particular domain or industry. This would involve training the model on large amounts of domain-specific text data and fine-tuning the model to the specific language and terminology used in that domain.
Another future direction is to develop ChatGPT models that can transfer knowledge from one domain to another, allowing for more efficient training and adaptation of language models. This involves developing transfer learning techniques enabling the model to generalize from one domain to another while preserving the domain-specific language and context. Domain-specific language models could be used to address specific challenges in different disciplines. For example, ChatGPT could be used in healthcare to develop models for medical diagnosis, drug discovery, or patient monitoring. In finance, it could be used to develop fraud detection, investment analysis, or risk management models. These applications require a deep understanding of domain-specific language and context, making ChatGPT an ideal tool for tackling these challenges.
6. Conclusions
In conclusion, this survey presents a critical review of ChatGPT, its technical advancements, and its standing within the realm of conversational and generative AI. We have demystified the factors that contribute to ChatGPT’s exceptional performance and capabilities by thoroughly analyzing its innovations, establishing a taxonomy of recent research, and conducting a comparative analysis of its competitors. Moreover, we have identified and discussed the challenges and limitations of ChatGPT, emphasizing areas of improvement and unexplored research opportunities.
We believe this survey lays the groundwork for a deeper understanding of the trending ChatGPT in generative AI and will serve as a valuable reference for researchers and practitioners seeking to harness the power of ChatGPT in their applications or address its gaps as part of ongoing development.
Funding
Prince Sultan University.
References
- A. S. George and A. H. George, “A review of chatgpt ai’s impact on several business sectors,” Partners Universal International Innovation Journal, vol. 1, no. 1, pp. 9–23, 2023.
- M. Verma, “Integration of ai-based chatbot (chatgpt) and supply chain management solution to enhance tracking and queries response.
- K. Jeblick, B. Schachtner, J. Dexl, A. Mittermeier, A. T. Stüber, J. Topalis, T. Weber, P. Wesp, B. Sabel, J. Ricke et al., “Chatgpt makes medicine easy to swallow: An exploratory case study on simplified radiology reports,” arXiv preprint arXiv:2212.14882, 2022.
- S. Frieder, L. Pinchetti, R.-R. Griffiths, T. Salvatori, T. Lukasiewicz, P. C. Petersen, A. Chevalier, and J. Berner, “Mathematical capabilities of chatgpt,” arXiv preprint arXiv:2301.13867, 2023.
- S. Shahriar and K. Hayawi, “Let’s have a chat! a conversation with chatgpt: Technology, applications, and limitations,” arXiv preprint arXiv:2302.13817, 2023.
- A. Lecler, L. Duron, and P. Soyer, “Revolutionizing radiology with gpt-based models: Current applications, future possibilities and limitations of chatgpt,” Diagnostic and Interventional Imaging, 2023.
- R. Omar, O. Mangukiya, P. Kalnis, and E. Mansour, “Chatgpt versus traditional question answering for knowledge graphs: Current status and future directions towards knowledge graph chatbots,” arXiv preprint arXiv:2302.06466, 2023. C.
- A. Haleem, M. Javaid, and R. P. Singh, “An era of chatgpt as a significant futuristic support tool: A study on features, abilities, and challenges,” BenchCouncil Transactions on Benchmarks, Standards and Evaluations, p. 100089, 2023.
- T. B. Brown, B. Mann, N. Ryder, M. Subbiah, J. Kaplan, P. Dhariwal, A. Neelakantan, P. Shyam, G. Sastry, A. Askell, S. Agarwal, A. Herbert-Voss, G. Krueger, T. Henighan, R. Child, A. Ramesh, D. M. Ziegler, J. Wu, C. Winter, C. Hesse, M. Chen, E. Sigler, M. Litwin, S. Gray, B. Chess, J. Clark, C. Berner, S. McCandlish, A. Radford, I. Sutskever, and D. Amodei, “Language models are few-shot learners,” CoRR, vol. abs/2005.14165, 2020.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. u. Kaiser, and I. Polosukhin, “Attention is all you need,” in Advances in Neural Information Processing Systems, I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, Eds., vol. 30. Curran Associates, Inc., 2017. [Online]. Available online: https://proceedings.neurips.cc/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf.
- J. Devlin, M.-W. Chang, K. Lee, and K. Toutanova, “Bert: Pre-training of deep bidirectional transformers for language understanding,” arXiv preprint arXiv:1810.04805, 2018.
- A. Radford, K. Narasimhan, T. Salimans, and I. Sutskever, “Improving language understanding by generative pre-training,” URL https://s3-us-west-2. amazonaws. com/openai-assets/researchcovers/languageunsupervised/language_understanding_paper. pdf, 2018.
- P. F. Christiano, J. Leike, T. Brown, M. Martic, S. Legg, and D. Amodei, “Deep reinforcement learning from human preferences,” Advances in neural information processing systems, vol. 30, 2017.
- L. Ouyang, J. Wu, X. Jiang, D. Almeida, C. L. Wainwright, P. Mishkin, C. Zhang, S. Agarwal, K. Slama, A. Ray, J. Schulman, J. Hilton, F. Kelton, L. Miller, M. Simens, A. Askell, P. Welinder, P. Christiano, J. Leike, and R. Lowe, “Training language models to follow instructions with human feedback,” 2022.
- H. H. Thorp, “Chatgpt is fun, but not an author,” Science, vol. 379, no. 6630, pp. 313–313, 2023.
- R. S. Sutton and A. G. Barto, Reinforcement learning: An introduction. MIT press, 2018.
- J. Ho and S. Ermon, “Generative adversarial imitation learning,” Advances in neural information processing systems, vol. 29, 2016.
- J. Schulman, S. Levine, P. Abbeel, M. Jordan, and P. Moritz, “Trust region policy optimization,” in International conference on machine learning, 2015, pp. 1889–1897.
- V. Mnih, A. P. Badia, M. Mirza, A. Graves, T. Lillicrap, T. Harley, D. Silver, and K. Kavukcuoglu, “Asynchronous methods for deep reinforcement learning,” in International conference on machine learning, 2016, pp. 1928–1937.
- J. Schulman, F. Wolski, P. Dhariwal, A. Radford, and O. Klimov, “Proximal policy optimization algorithms,” arXiv preprint arXiv:1707.06347, 2017.
- Y. Wang, H. He, and X. Tan, “Truly proximal policy optimization,” in Uncertainty in Artificial Intelligence. PMLR, 2020, pp. 113–122.
- A. Glaese, N. McAleese, M. Trębacz, J. Aslanides, V. Firoiu, T. Ewalds, M. Rauh, L. Weidinger, M. Chadwick, P. Thacker et al., “Improving alignment of dialogue agents via targeted human judgements,” arXiv preprint arXiv:2209.14375, 2022.
- Y. Bai, A. Jones, K. Ndousse, A. Askell, A. Chen, N. DasSarma, D. Drain, S. Fort, D. Ganguli, T. Henighan et al., “Training a helpful and harmless assistant with reinforcement learning from human feedback,” arXiv preprint arXiv:2204.05862, 2022.
- N. Stiennon, L. Ouyang, J. Wu, D. Ziegler, R. Lowe, C. Voss, A. Radford, D. Amodei, and P. F. Christiano, “Learning to summarize with human feedback,” Advances in Neural Information Processing Systems, vol. 33, pp. 3008–3021, 2020.
- V. Malhotra, “Google introduces bard ai as a rival to chatgpt,” 2023, https://beebom.com/google-bard-chatgpt-rival-introduced/.
- S. Garg, “What is chatsonic, and how to use it?” 2023, https://writesonic.com/blog/what-is-chatsonic/.
- Jasper, “Jasper chat - ai chat assistant,” 2023, https://www.jasper.ai/.
- OpenAI, “Welcome to openai,” 2023, https://platform.openai.com/overview.
- C. AI, “Caktus - open writing with ai,” 2023, https://www.caktus.ai/caktus_student/.
- E. Kuyda, “What is chatsonic, and how to use it?” 2023, https://help.replika.com/hc/en-us/articles/115001070951-What-is-Replika-.
- C. Research, “Chai gpt - ai more human, less filters,” 2023, https://www.chai-research.com/.
- Rytr, “Rytr - take your writing assistant,” 2023, https://rytr.me/.
- Peppertype.ai, “Peppertype.ai - your virtual content assistant,” 2023, https://www.peppertype.ai/.
- B. Guo, X. Zhang, Z. Wang, M. Jiang, J. Nie, Y. Ding, J. Yue, and Y. Wu, “How close is chatgpt to human experts? comparison corpus, evaluation, and detection,” arXiv preprint arXiv:2301.07597, 2023.
- Y. Bang, S. Cahyawijaya, N. Lee, W. Dai, D. Su, B. Wilie, H. Lovenia, Z. Ji, T. Yu, W. Chung et al., “A multitask, multilingual, multimodal evaluation of chatgpt on reasoning, hallucination, and interactivity,” arXiv preprint arXiv:2302.04023, 2023.
- N. Muennighoff, “Sgpt: Gpt sentence embeddings for semantic search,” arXiv preprint arXiv:2202.08904, 2022.
- C. Zhou, Q. Li, C. Li, J. Yu, Y. Liu, G. Wang, K. Zhang, C. Ji, Q. Yan, L. He et al., “A comprehensive survey on pretrained foundation models: A history from bert to chatgpt,” arXiv preprint arXiv:2302.09419, 2023.
- C. Qin, A. Zhang, Z. Zhang, J. Chen, M. Yasunaga, and D. Yang, “Is chatgpt a general-purpose natural language processing task solver?” arXiv preprint arXiv:2302.06476, 2023.
- M. Ortega-Martín, Ó. García-Sierra, A. Ardoiz, J. Álvarez, J. C. Armenteros, and A. Alonso, “Linguistic ambiguity analysis in chatgpt,” arXiv preprint arXiv:2302.06426, 2023.
- A. Borji, “A categorical archive of chatgpt failures,” arXiv preprint arXiv:2302.03494, 2023.
- X. Yang, Y. Li, X. Zhang, H. Chen, and W. Cheng, “Exploring the limits of chatgpt for query or aspect-based text summarization,” arXiv preprint arXiv:2302.08081, 2023.
- W. Jiao, W. Wang, J.-t. Huang, X. Wang, and Z. Tu, “Is chatgpt a good translator? a preliminary study,” arXiv preprint arXiv:2301.08745, 2023.
- J. Kocoń, I. Cichecki, O. Kaszyca, M. Kochanek, D. Szydło, J. Baran, J. Bielaniewicz, M. Gruza, A. Janz, K. Kanclerz et al., “Chatgpt: Jack of all trades, master of none,” arXiv preprint arXiv:2302.10724, 2023.
- D. L. Mann, “Artificial intelligence discusses the role of artificial intelligence in translational medicine: A jacc: Basic to translational science interview with chatgpt,” Basic to Translational Science, 2023.
- F. Antaki, S. Touma, D. Milad, J. El-Khoury, and R. Duval, “Evaluating the performance of chatgpt in ophthalmology: An analysis of its successes and shortcomings,” medRxiv, pp. 2023–01, 2023.
- T. H. Kung, M. Cheatham, A. Medenilla, C. Sillos, L. De Leon, C. Elepaño, M. Madriaga, R. Aggabao, G. Diaz-Candido, J. Maningo et al., “Performance of chatgpt on usmle: Potential for ai-assisted medical education using large language models,” PLOS Digital Health, vol. 2, no. 2, p. e0000198, 2023.
- J. Dahmen, M. Kayaalp, M. Ollivier, A. Pareek, M. T. Hirschmann, J. Karlsson, and P. W. Winkler, “Artificial intelligence bot chatgpt in medical research: the potential game changer as a double-edged sword,” pp. 1–3, 2023.
- M. R. King, “The future of ai in medicine: a perspective from a chatbot,” Annals of Biomedical Engineering, pp. 1–5, 2022.
- K. Bhattacharya, A. S. Bhattacharya, N. Bhattacharya, V. D. Yagnik, P. Garg, and S. Kumar, “Chatgpt in surgical practice—a new kid on the block,” Indian Journal of Surgery, pp. 1–4, 2023.
- T. B. Arif, U. Munaf, and I. Ul-Haque, “The future of medical education and research: Is chatgpt a blessing or blight in disguise?” p. 2181052, 2023.
- L. B. Anderson, D. Kanneganti, M. B. Houk, R. H. Holm, and T. R. Smith, “Generative ai as a tool for environmental health research translation,” medRxiv, pp. 2023–02, 2023.
- N. Kurian, J. Cherian, N. Sudharson, K. Varghese, and S. Wadhwa, “Ai is now everywhere,” British Dental Journal, vol. 234, no. 2, pp. 72–72, 2023.
- S. Wang, H. Scells, B. Koopman, and G. Zuccon, “Can chatgpt write a good boolean query for systematic review literature search?” arXiv preprint arXiv:2302.03495, 2023.
- A. Graf and R. E. Bernardi, “Chatgpt in research: Balancing ethics, transparency and advancement.” Neuroscience, pp. S0306–4522, 2023.
- P. Hacker, A. Engel, and M. Mauer, “Regulating chatgpt and other large generative ai models,” arXiv preprint arXiv:2302.02337, 2023.
- M. Khalil and E. Er, “Will chatgpt get you caught? rethinking of plagiarism detection,” arXiv preprint arXiv:2302.04335, 2023.
- T. Y. Zhuo, Y. Huang, C. Chen, and Z. Xing, “Exploring ai ethics of chatgpt: A diagnostic analysis,” arXiv preprint arXiv:2301.12867, 2023.
- X. Chen, “Chatgpt and its possible impact on library reference services,” Internet Reference Services Quarterly, pp. 1–9, 2023.
- T. Susnjak, “Chatgpt: The end of online exam integrity?” arXiv preprint arXiv:2212.09292, 2022.
- A. Tlili, B. Shehata, M. A. Adarkwah, A. Bozkurt, D. T. Hickey, R. Huang, and B. Agyemang, “What if the devil is my guardian angel: Chatgpt as a case study of using chatbots in education,” Smart Learning Environments, vol. 10, no. 1, pp. 1–24, 2023.
- M. Salvagno, F. S. Taccone, A. G. Gerli et al., “Can artificial intelligence help for scientific writing?” Critical Care, vol. 27, no. 1, pp. 1–5, 2023.
- M. R. King and chatGPT, “A conversation on artificial intelligence, chatbots, and plagiarism in higher education,” Cellular and Molecular Bioengineering, pp. 1–2, 2023.
- S. A. Prieto, E. T. Mengiste, and B. G. de Soto, “Investigating the use of chatgpt for the scheduling of construction projects,” arXiv preprint arXiv:2302.02805, 2023.
- M. Dowling and B. Lucey, “Chatgpt for (finance) research: The bananarama conjecture,” Finance Research Letters, p. 103662, 2023.
- R. Gozalo-Brizuela and E. C. Garrido-Merchan, “Chatgpt is not all you need. a state of the art review of large generative ai models,” arXiv preprint arXiv:2301.04655, 2023.
- A. Baki Kocaballi, “Conversational ai-powered design: Chatgpt as designer, user, and product,” arXiv e-prints, pp. arXiv–2302, 2023.
- H. Harkous, K. Fawaz, K. G. Shin, and K. Aberer, “Pribots: Conversational privacy with chatbots,” in Workshop on the Future of Privacy Notices and Indicators, at the Twelfth Symposium on Usable Privacy and Security, SOUPS 2016, no. CONF, 2016.
- M. Hasal, J. Nowaková, K. Ahmed Saghair, H. Abdulla, V. Snášel, and L. Ogiela, “Chatbots: Security, privacy, data protection, and social aspects,” Concurrency and Computation: Practice and Experience, vol. 33, no. 19, p. e6426, 2021.
- E. Ruane, A. Birhane, and A. Ventresque, “Conversational ai: Social and ethical considerations.” in AICS, 2019, pp. 104–115.
- N. Park, K.N. Park, K. Jang, S. Cho, and J. Choi, “Use of offensive language in human-artificial intelligence chatbot interaction: The effects of ethical ideology, social competence, and perceived humanlikeness,” Computers in Human Behavior, vol. 121, p. 106795, 2021.
- H. Beattie, L. Watkins, W. H. Robinson, A. Rubin, and S. Watkins, “Measuring and mitigating bias in ai-chatbots,” in 2022 IEEE International Conference on Assured Autonomy (ICAA). IEEE, 2022, pp. 117–123.
- Y. K. Dwivedi, N. Kshetri, L. Hughes, E. L. Slade, A. Jeyaraj, A. K. Kar, A. M. Baabdullah, A. Koohang, V. Raghavan, M. Ahuja et al., ““so what if chatgpt wrote it?” multidisciplinary perspectives on opportunities, challenges and implications of generative conversational ai for research, practice and policy,” International Journal of Information Management, vol. 71, p. 102642, 2023.
Figure 1.
Google Search Interest Over Time: "ChatGPT", "Transformers", "Computer Vision", "Natural Language Processing".
Figure 1.
Google Search Interest Over Time: "ChatGPT", "Transformers", "Computer Vision", "Natural Language Processing".
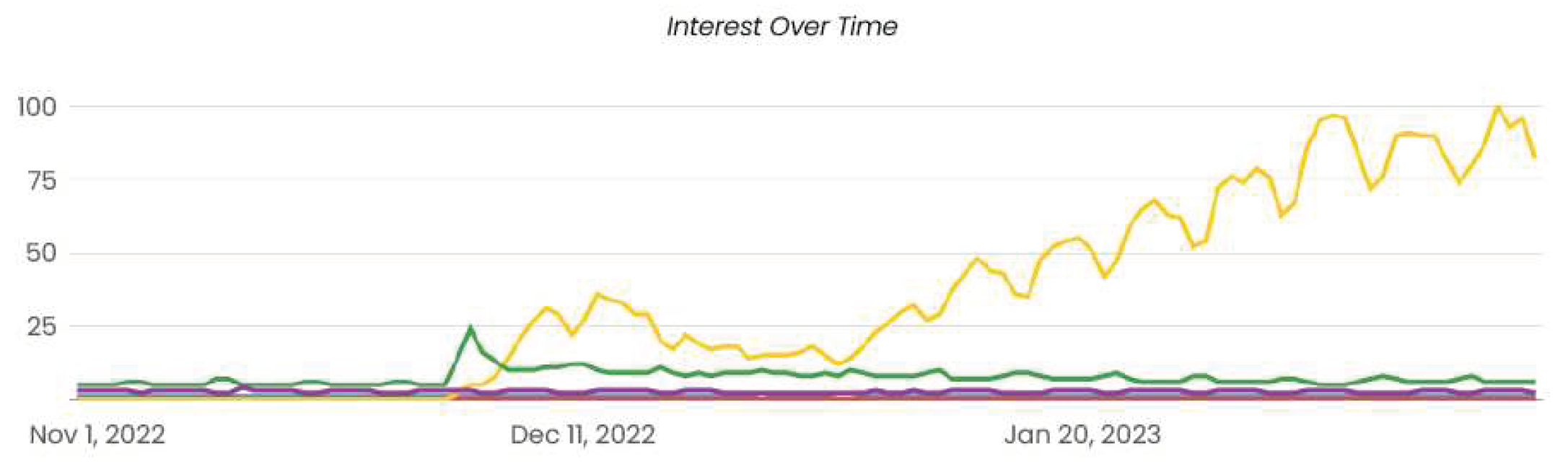
Figure 2.
Distribution of selected articles based on publishers.
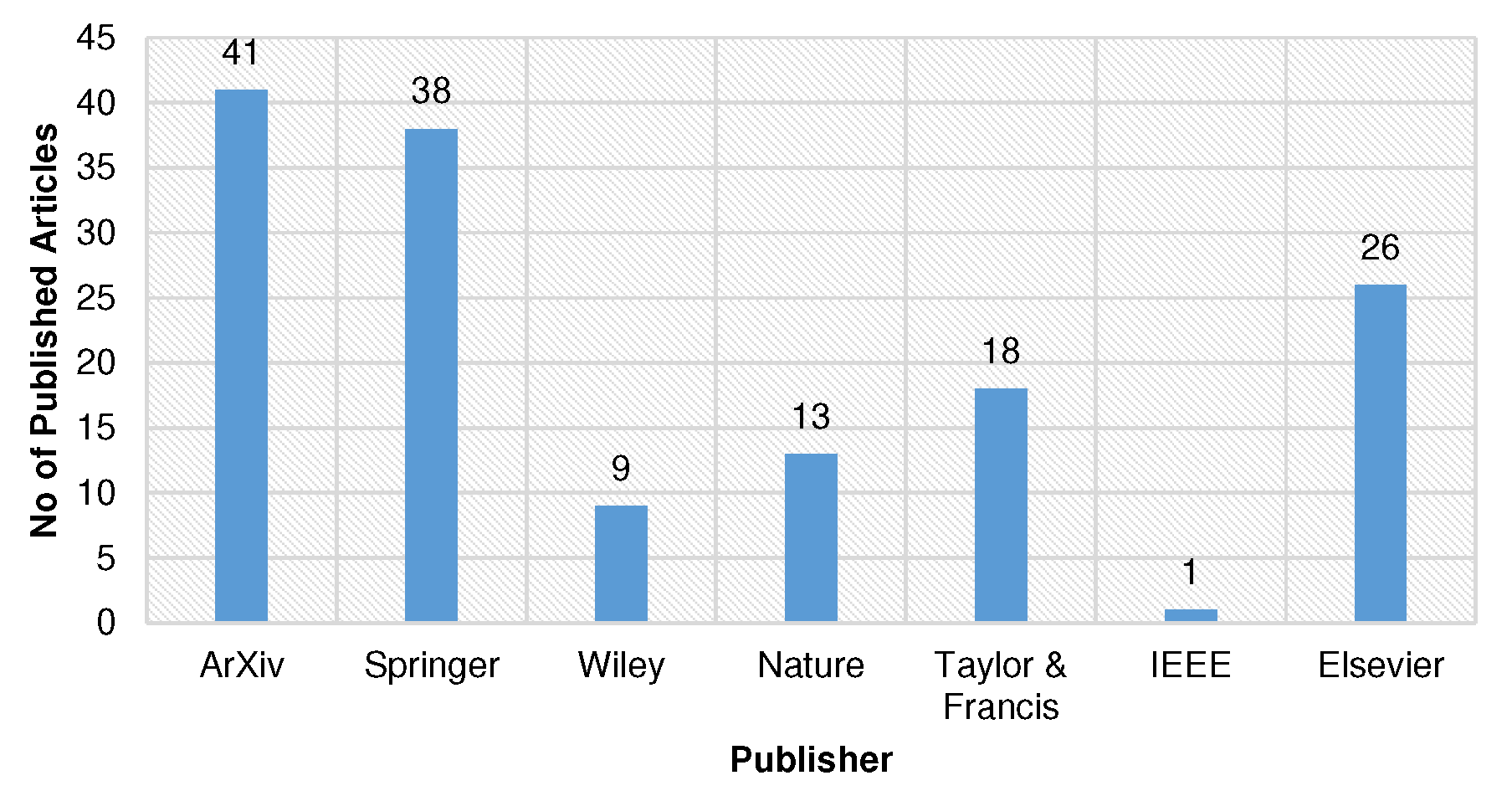
Figure 3.
Distribution of selected articles based on article type.
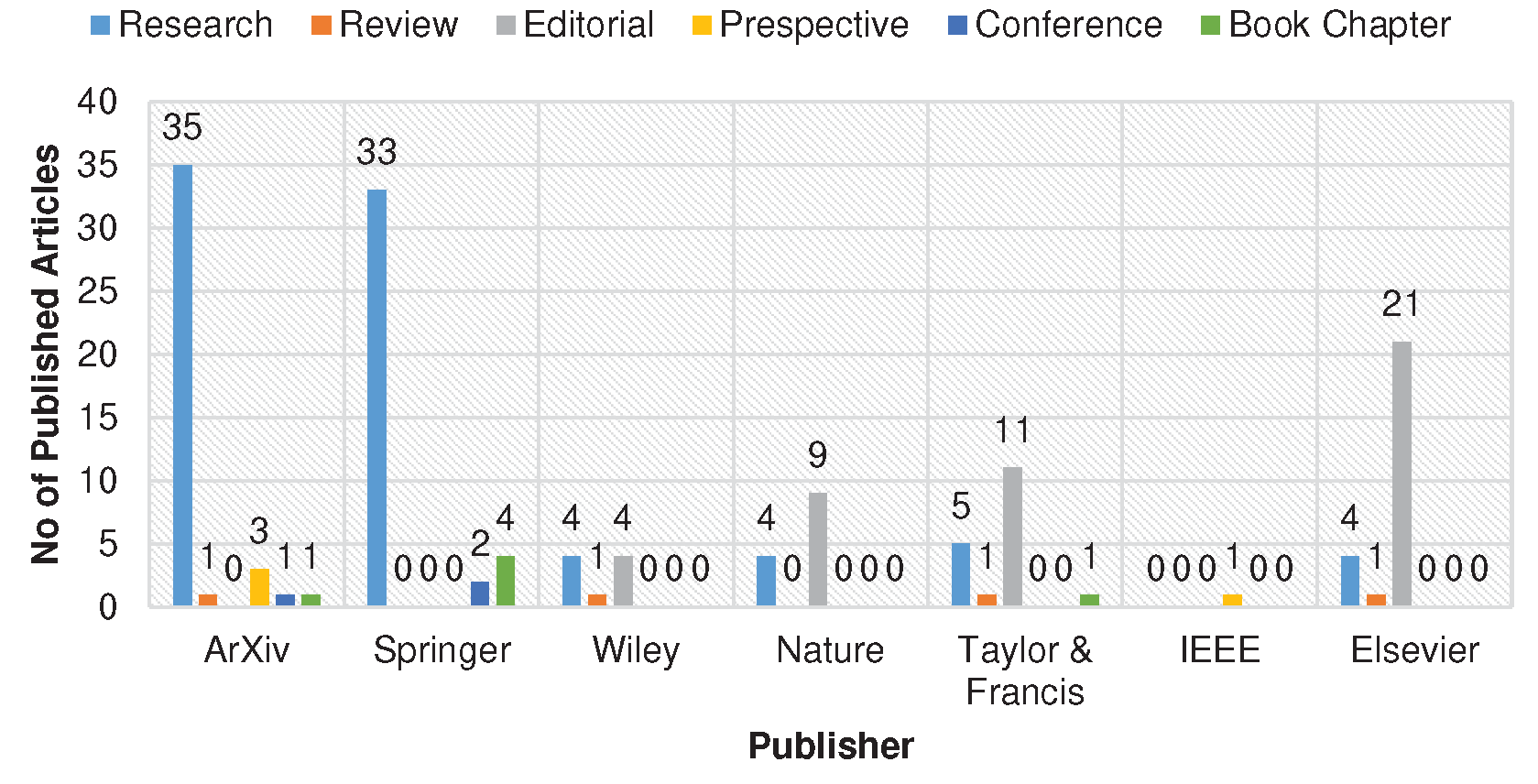
Figure 4.
The Transformers Architecture as defined in [10] for Machine Translation.
Figure 4.
The Transformers Architecture as defined in [10] for Machine Translation.
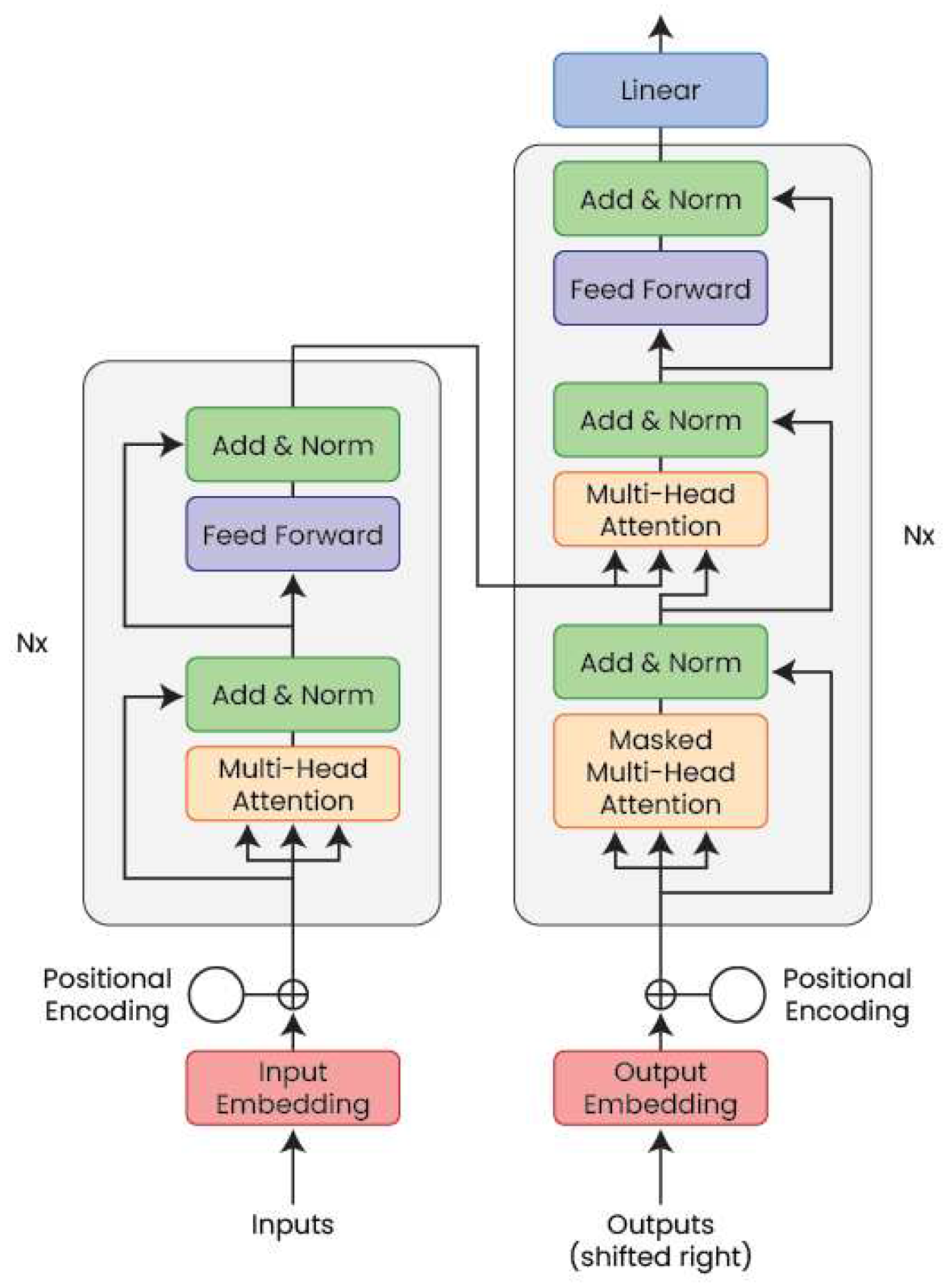
Figure 5.
The Transformers Architecture as defined in GPT [12].
Figure 5.
The Transformers Architecture as defined in GPT [12].
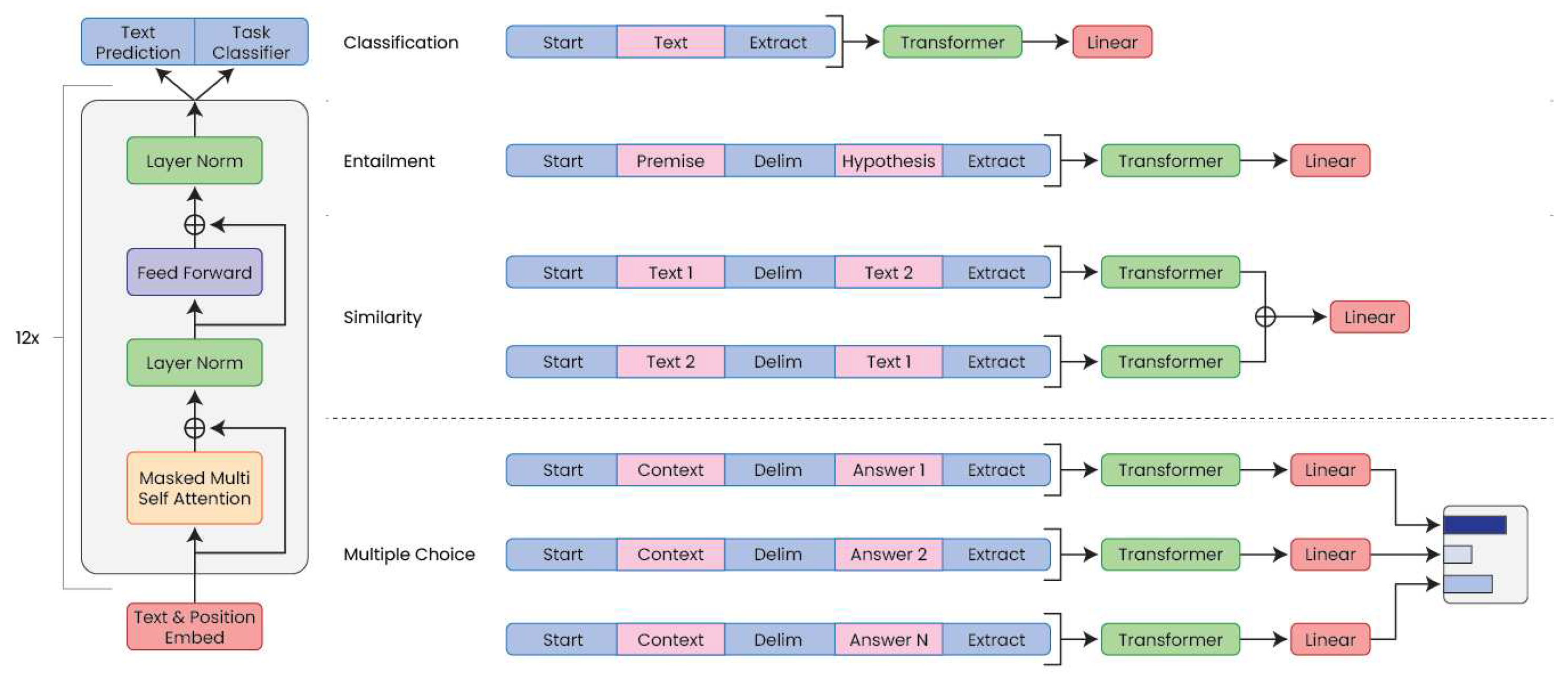
Figure 6.
Self-Attention Module Architecture [12].
Figure 6.
Self-Attention Module Architecture [12].
Figure 7.
Basic RL model.
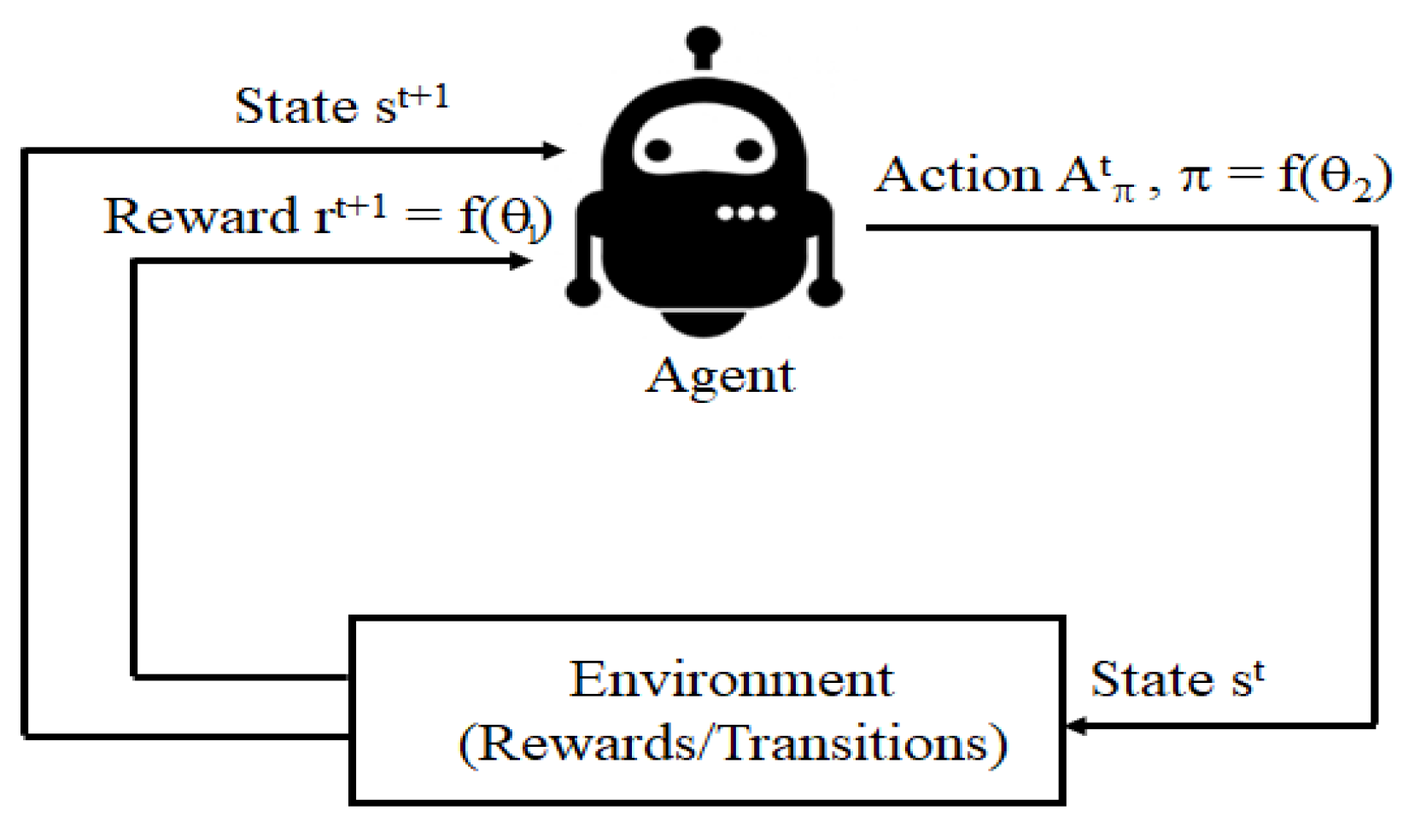
Figure 8.
Differences between AI-based and human-based text summarization processes.
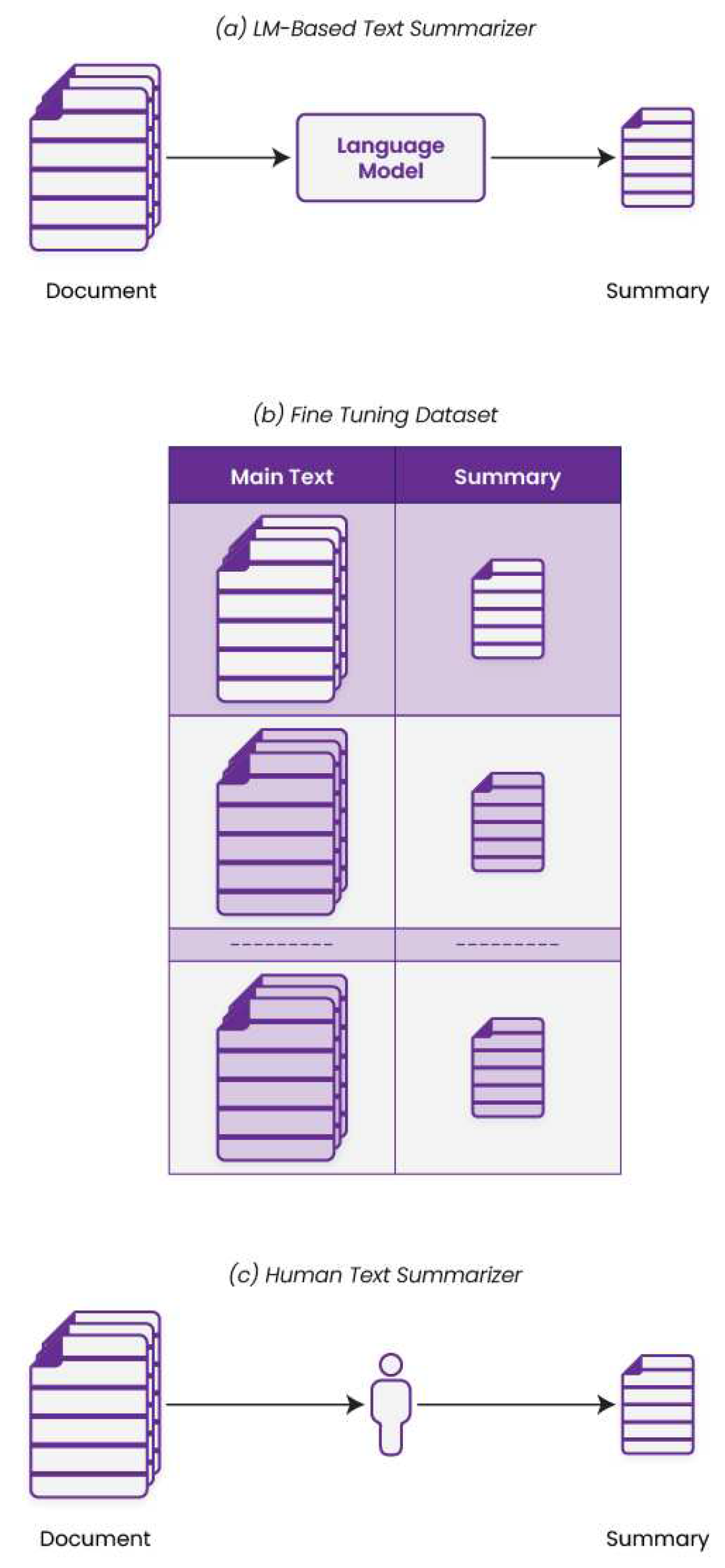
Figure 9.
Reward-based policy training.
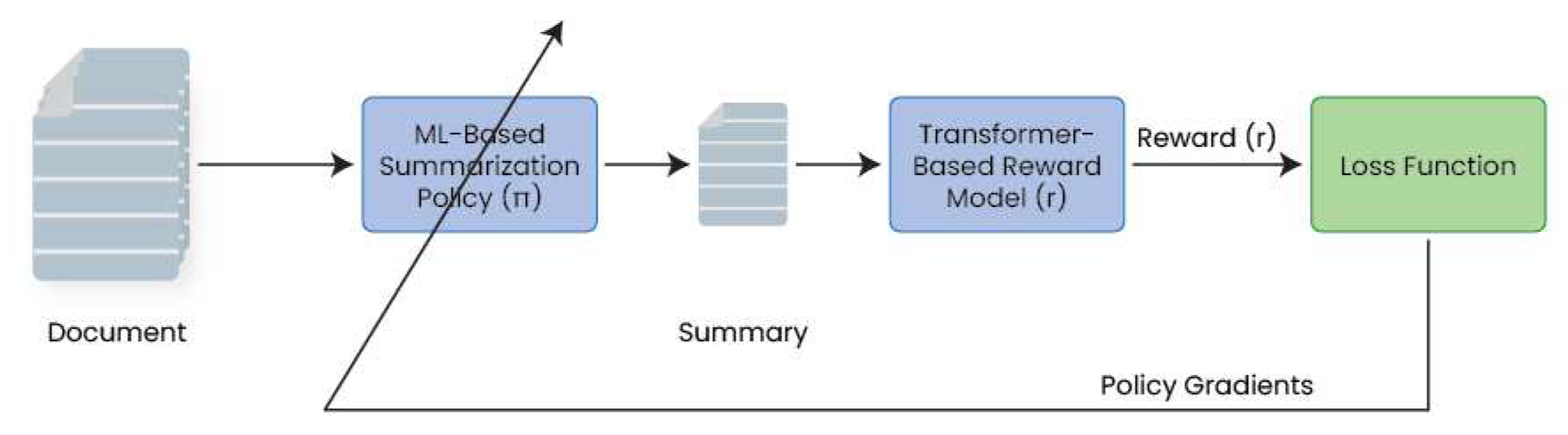
Figure 10.
Reward module training.
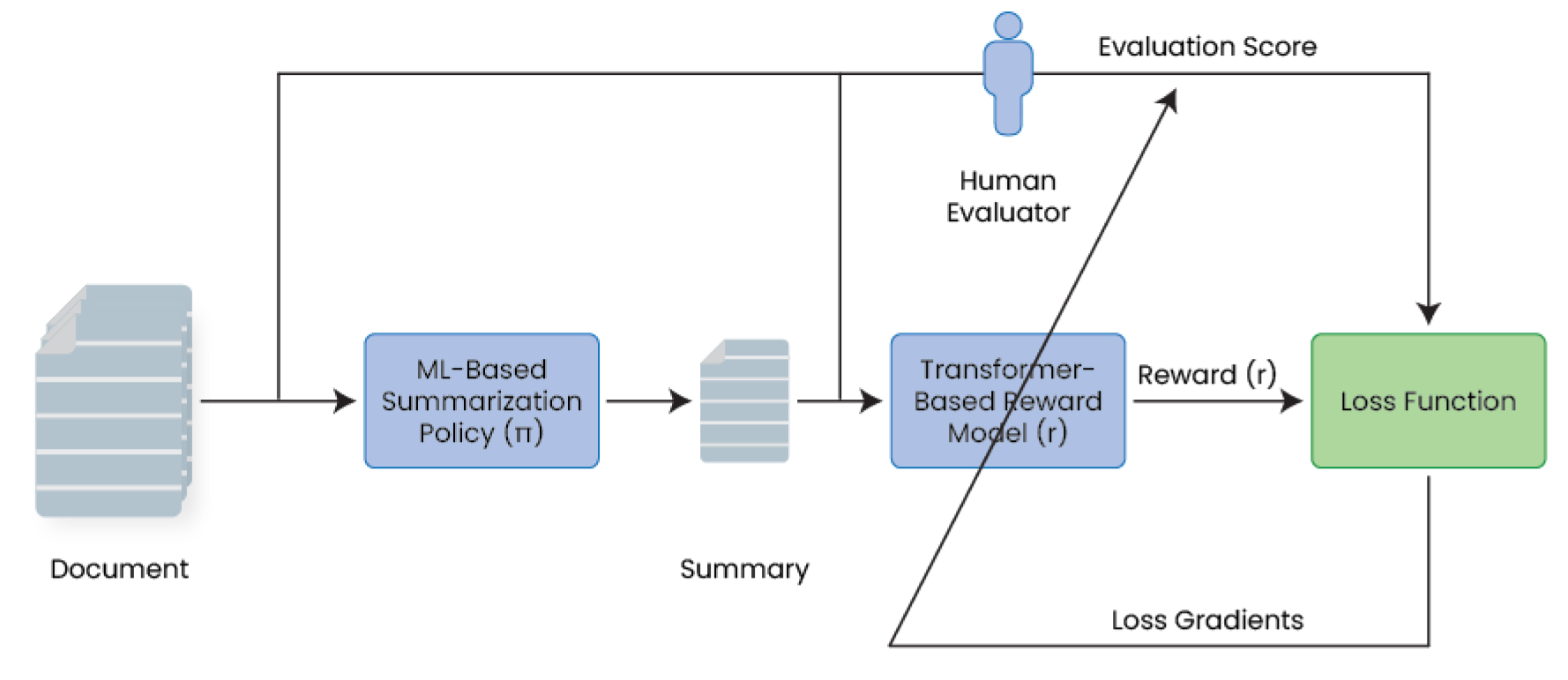
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
State-of-the-art in Open-domain Conversational AI: A Survey
Tosin Adewumi
et al.
,
2022
Enhancing Accuracy in Large Language Models Through Dynamic Real-Time Information Injection
Qian Ouyang
et al.
,
2023
A Testing Framework for AI Linguistic Systems (testFAILS)
Yulia Kumar
et al.
,
2023
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated
