Keywords: Bernoulli polynomials and numbers, Apostol-Bernoulli polynomials, Apostol-Euler polynomials, Generalized Apostol-Bernoulli polynomials
Turkish Journal of Analysis and Number Theory, 2013 1 (1),
pp 54-58.
DOI: 10.12691/tjant-1-1-11
Received October 15, 2013; Revised November 25, 2013; Accepted December 03, 2013
Copyright © 2013 Science and Education Publishing. All Rights Reserved.
1. Introduction, Definitions
Bernoulli polynomials play an important role in various expansions and approximation formulas which are useful both in analytic theory of numbers and the classical and the numerical analysis. These polynomials can be defined by various methods depending on the applications. There are six approaches to the theory of Bernoulli polynomials. We prefer here the definition by generating functions given by Euler [4].
The classical Bernoulli polynomials and the classical Euler polynomials are defined respectively as
 | (1.1) |
 | (1.2) |
The corresponding Bernoulli numbers  and Euler numbers
and Euler numbers  are given by
are given by
From (1.1) and (1.2), we easily derive that
 | (1.3) |
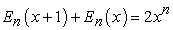 | (1.4) |
(for details, see [11, J. of App. Math., 153-163, 2003.">12, App. Math. Letter, 17, 375-380, 2004.">13]).
The generalized Apostol-Bernoulli polynomials  order
order  and the generalized Apostol-Euler polynomials
and the generalized Apostol-Euler polynomials  order
order  are defined respectively by the following generating functions
are defined respectively by the following generating functions
 | (1.5) |
 | (1.6) |
Recently, Srivastava et. al. in ([App. Math. Letter, 17, 375-380, 2004.">13, Russian J. of Math. Phys., 17, 251-261, 2010.">14, Taiwanese J. of Math., 15, 283-305, 2011.">15]) have investigated some new classes of Apostol-Bernoulli, Apostol-Euler polynomials with parameters a, b, and c. They gave some recurrence relations and proved some theorems.
For  one can obtain the classical polynomials (1.1) and (1.2). Other generalizations can be developed as well.
one can obtain the classical polynomials (1.1) and (1.2). Other generalizations can be developed as well.
Definition 1. [Natalini [12] and S. Chen et al. [3]] The generalized Bernoulli polynomials  are defined, in a suitable neigbourhood of
are defined, in a suitable neigbourhood of  by means of the generating functions
by means of the generating functions
 | (1.7) |
From (1.7) for  we obtain the generating function
we obtain the generating function  of classical Bernoulli polynomials
of classical Bernoulli polynomials  From (1.7) for
From (1.7) for  we obtain the generalized Bernoulli numbers
we obtain the generalized Bernoulli numbers 
Definition 2. [Kurt [9]] For  the generalized Bernoulli polynomials
the generalized Bernoulli polynomials  of order
of order  are defined by means of the generating function
are defined by means of the generating function
 | (1.8) |
in suitable neigbourhood of 
The case  was first introduced by Natalini and Bernardini [6]. For
was first introduced by Natalini and Bernardini [6]. For  we obtain classical Bernoulli polynomials.
we obtain classical Bernoulli polynomials.
By the same motivation, the generalized Euler polynomials  of order
of order  and generalized Euler numbers
and generalized Euler numbers  of order
of order  were defined by the author [10]
were defined by the author [10]
 | (1.9) |
and
 | (1.10) |
From (1.9) and (1.10) and for  we obtain classical Euler polynomials and classical Euler numbers respectively:
we obtain classical Euler polynomials and classical Euler numbers respectively:
By the same motivation, the generalized Genocchi polynomials of order
of order  and generalized Genocchi numbers
and generalized Genocchi numbers  of order
of order  can be defined as
can be defined as
 | (1.11) |
and
 | (1.12) |
2. New Classes of Generalized Apostol-Euler Polynomials and Apostol-Bernoulli Polynomials
The following definitions provide a natural generalization of the Apostol-Euler polynomials 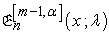 of order
of order  and the Apostol-Bernoulli polynomials
and the Apostol-Bernoulli polynomials  of order
of order  where
where 
Definition 3. We de.ne the generalized Bernoulli polynomials  of order
of order  and the generalized Euler polynomials
and the generalized Euler polynomials  of order
of order  respectively by
respectively by
 | (2.1) |
 | (2.2) |
and
 | (2.3) |
For  (2.1) reduces to (1.7).
(2.1) reduces to (1.7).
For  (2.1), (2.2) and (2.3) reduce to classical Bernoulli polynomial, classical Euler polynomial and classical Genocchi polynomial.
(2.1), (2.2) and (2.3) reduce to classical Bernoulli polynomial, classical Euler polynomial and classical Genocchi polynomial.
From (2.1), (2.2) and (2.3), we obtain
and
Theorem 1. Let  Then the generalized Apostol-Bernoulli polynomials
Then the generalized Apostol-Bernoulli polynomials  and the generalized Apostol-Euler polynomials
and the generalized Apostol-Euler polynomials  satisfy the following relations
satisfy the following relations
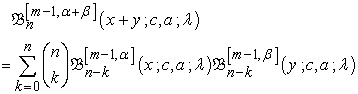 | (2.4) |
 | (2.5) |
and
 | (2.6) |
respectively.
Proof. Considering the generating function (2.1) and comparing the coefficients of  in the both sides of the above equation, we arrive at (2.4). Proof of (2.5) and (2.6) are similar.
in the both sides of the above equation, we arrive at (2.4). Proof of (2.5) and (2.6) are similar.
Theorem 2. The generalized Apostol-Bernoulli polynomials  satisfy the following recurrence relation:
satisfy the following recurrence relation:
 | (2.7) |
Proof. Considering the expression  and using generating function (2.1), the proof follows.
and using generating function (2.1), the proof follows.
Corollary 1. The generalized Apostol-Euler polynomials  satisfy the following recurrence relation:
satisfy the following recurrence relation:
 | (2.8) |
Theorem 3. There is the following relation between the generalized Apostol-Bernoulli polynomials  for
for  and the generalized Apostol-Euler polynomials
and the generalized Apostol-Euler polynomials  for
for 
 | (2.9) |
Proof. We take  and
and  instead of
instead of  and
and  respectively. We write as:
respectively. We write as:
Comparing the coefficients of  , we obtain (2.9).
, we obtain (2.9).
Theorem 4. The generalized Apostol-Bernoulli polynomials  satisfy the following recurrence relation:
satisfy the following recurrence relation:
 | (2.10) |
Proof. From (2.1) for  we write as
we write as
 | (2.11) |
 | (2.12) |
We put (2.12) in the right hand side of (2.11). Then
If we make necessary operations in the last equation and comparing the coefficients of  we arrive (2.10).
we arrive (2.10).
Theorem 5. The following relations hold true:
 | (2.13) |
and
 | (2.14) |
Proof. From (2.1) for 
Comparing the coefficients of  we obtain (2.13).
we obtain (2.13).
For the proof of (2.14), we write
Comparing the coefficients of  we arrived to result.
we arrived to result.
Corollary 2. The new generalized Bernoulli polynomials  for
for  and the new generalized Euler polynomials
and the new generalized Euler polynomials  for
for  satisfy the following Raabe relations:
satisfy the following Raabe relations:
 | (2.15) |
and
 | (2.16) |
Proof. We put  in (2.1),
in (2.1),
From the last equality, we have (2.15).
Second equation of this corollary can be obtained similarly, so we omit it.
Acknowledgements
This paper was supported by the Scientific Research Project Administration of Akdeniz University.
References
| [1] | A. Bagdasaryan and S. Araci, Some new identities on the Apostol-Bernoulli polynomials higher order derived from Bernoulli basis, arXiv:1311.4148 [math.NT]. |
|  In article In article | |
| |
| [2] | G. Bretti and P. E. Ricci, Multidimensional extensions of the Bernoulli and Appell polynomials, Taiwanese J. of Math. 8, 415-428, 2004. |
|  In article In article | |
| |
| [3] | S. Chen, Yi Chai and Q.-M. Luo, An extension of generalized Apostol-Euler polynomials, Advances in Difference Equation. |
|  In article In article | |
| |
| [4] | F. Costabile, F. Dellaccio and M. I. Gualtieri, A new approach to Bernoulli polynomials, Rendi. di. Math. Series VII, 26, 1-12, 2006. |
|  In article In article | |
| |
| [5] | S. Gaboury and B. Kurt, Some relations involving Hermite-based Apostol-Genocchi polynomials, App. Math. Sci., 82, 4091-4102, 2012. |
|  In article In article | |
| |
| [6] | Y. He and C. Wang, Some formulae of products of the Apostol-Bernoulli and Apostol-Euler polynomials, Discrete Dynamics in Nature and Society, Article ID 927953, 11 pages, 2012. |
|  In article In article | |
| |
| [7] | T. Kim, Some identities for the Bernoulli, Euler and Genocchi numbers and polynomials, Adv. Stud. Contemp. Math. 20, 18-23, 2010. |
|  In article In article | |
| |
| [8] | T. Kim, T. Mansour, S.-H. Rim and S.-H. Lee, Apostol-Euler polynomials arising from umbral calculus, Advances in Difference Equations 2013, 2013:300. |
|  In article In article | |
| |
| [9] | B. Kurt, A further generalization of the Bernoulli polynomials and on the 2D-Bernoulli polynomials Bn2(x,y), App. Math. Sci., 47, 2315-2322, 2010. |
|  In article In article | |
| |
| [10] | B. Kurt, A further generalization of the Euler polynomials and on the 2D-Euler polynomials, Proc. Jang. Math. Soc., 15, 389-394, 2012. |
|  In article In article | |
| |
| [11] | Q.-M. Luo, The multiplication formulas for the Apostol-Bernoulli and Apostol-Euler polynomials of higher order, Int. Trans. Spec. Func. Vol 20(5), 377-391, 2009. |
|  In article In article | CrossRef |
| |
| [12] | P. Natalini and A. Bernardini, A Generalization of the Bernoulli polynomials, J. of App. Math., 153-163, 2003. |
|  In article In article | |
| |
| [13] | H. M. Srivastava and A. Pinter, Remarks on some relationships between the Bernoulli and Euler polynomials, App. Math. Letter, 17, 375-380, 2004. |
|  In article In article | CrossRef |
| |
| [14] | H. M. Srivastava, M. Garg and S. Choudhary, A new generalization of the Bernoulli and related polynomials, Russian J. of Math. Phys., 17, 251-261, 2010. |
|  In article In article | CrossRef |
| |
| [15] | H. M. Srivastava, M. Garg and S. Choudhary, Some new families of neralized Euler and Genocchi polynomials, Taiwanese J. of Math., 15, 283-305, 2011. |
|  In article In article | |
| |
| [16] | R. Trembly, S. Gaboury and B.-J. Fugére, A new class of generalized Apostol-Bernoulli polynomials and some analogues of the Srivastava-Pinter addition theorem, Applied Math. Letter, 24, 1888-1893, 2011. |
|  In article In article | CrossRef |
| |
| [17] | R. Trembly, S. Gaboury and B.-J. Fugére, Some new classes of generalized Apostol-Euler and Apostol-Genocchi polynomials, Inter. J. of Math. and Math. Sci., 2012. |
|  In article In article | |
| |