Abstract
Non-von-Neumann computing architectures and deep learning training models have sparked a new computational era where neurons are forming the main architectural backbone and vector, matrix and tensor multiplications comprise the basic mathematical toolbox. This paradigm shift has triggered a new race among hardware technology candidates; within this frame, the field of neuromorphic photonics promises to convolve the targeted algebraic portfolio along a computational circuitry with unique speed, parallelization, and energy efficiency advantages. Fueled by the inherent energy efficient analog matrix multiply operations of optics, the staggering advances of photonic integration and the enhanced multiplexing degrees offered by light, neuromorphic photonics has stamped the resurgence of optical computing brining a unique perspective in low-energy and ultra-fast linear algebra functions. However, the field of neuromorphic photonics has relied so far on two basic architectural schemes, i.e., coherent linear optical circuits and incoherent WDM approaches, where wavelengths have still not been exploited as a new mathematical dimension. In this paper, we present a radically new approach for promoting the synergy of WDM with universal linear optics and demonstrate a new, high-fidelity crossbar-based neuromorphic photonic platform, able to support matmul with multidimensional operands. Going a step further, we introduce the concept of programmable input and weight banks, supporting in situ reconfigurability, forming in this way the first WDM-equipped universal linear optical operator and demonstrating different operational modes like matrix-by-matrix and vector-by-tensor multiplication. The benefits of our platform are highlighted in a fully convolutional neural network layout that is responsible for parity identification in the MNIST handwritten digit dataset, with physical layer simulations revealing an accuracy of ∼94%, degraded by only 2% compared to respective results obtained when executed entirely by software. Finally, our in-depth analysis provides the guidelines for neuromorphic photonic processor performance improvement, revealing along the way that 4 bit quantization is sufficient for inputs, whereas the weights can be implemented with as low as 2 bits of precision, offering substantial benefits in terms of driving circuitry complexity and energy savings.
Export citation and abstract BibTeX RIS
Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Across diverse spectrum of applications, from object recognition and live tracking, natural language processing and generation (NLP and NLG), market dynamics prediction, to assistance in medical diagnostics, deep learning (DL) has offered a pathway to quickly create value from vast data repositories [1]. The feedback is positive—the more data is made available to the model, the better it will be at analyzing it, albeit, at the cost of increased complexity [2]. Looking at the NLPs as one of the most demanding use-cases, we are witnessing the number of model parameters skyrocketing from a shy of a 100 million (ELMo) only recently, in 2018, to more than half a trillion (Megatron-Turing NLG) in 2021 [3]. Specialized electronic hardware is continuously being developed to raise to the challenge of efficiently implementing present-day's DL models, extending from more generic GPUs to TPUs and FPGAs up to task-specific ASICs. The success of GPUs and TPUs in DL model implementations [4] can be attributed to their programmable hardware together with their ability to process the data in parallel, which is especially important in large-scale matrix multiplication (matmul) encountered in many artificial intelligence (AI) workloads. One of the examples is image recognition and classification, where multilayer convolutional neural networks (CNNs) demand applying the same kernel time after time during feature extraction, a task that greatly benefits from parallelization [5]. However, these advances alone do not seem to suffice, since, to efficiently tackle any NN implementation in practice, a paradigm shift is required from the ubiquitous von-Neumann architectures to in-memory computing.
When designing future-proof neuromorphic solutions, simultaneous improvement along three axes should be targeted: efficiency, flexibility, and performance. Analog crossbars (Xbars) have been found to outperform other competitors in this triple-axis optimization path, offering a single step matmul operation, and thus being suited for both inference and training at both the edge of a computing network and in data centers [1]. Having most real-world information analog in nature supports the trend of transitioning from digital domain to the analog one, especially in the light of recent advances in low precision [6] and noise-resilient training algorithms [7–11]. The superiority of the electronic crossbars has already been recognized by Syntiant [12], MemryX [13] and Mythic [14], with photonic platforms striving to produce an equivalent circuit for analog neuromorphic photonic setups, as shown by the works of Lightmatter [15, 16] and Lightelligence [17, 18] in commercial-grade large-scale coherent photonic integrated circuits (PICs).
Photonics, as a naturally analog platform, can offer multiple options for parallelization, such as wavelength-(WDM), mode-(MDM), or polarization division multiplexing (PDM) and challenges the supremacy of electronics in the field of neuromorphic computing. Recent years have brought a great variety of photonic neuromorphic prototypes, many of which have been experimentally demonstrated primarily for inference purposes [18–31], with their computational speed (compute rate) per axon shown in figure 1. These have relied on different approaches to achieve multiply-accumulate (MAC) operations, pushing the boundaries of energy and area efficiencies toward a few fJ/MAC and beyond TMAC/sec/mm2 [32, 33]. When speaking of integrated solutions, two main architectural directions can be observed: (i) coherent, which harnesses the interference for matmul using a single wavelength and is compatible with both optical and electro-optical (E/O) activations, and (ii) WDM or incoherent, which uses at least one different wavelength per axon for computation and typically relies on a photodiode (PD) for signal aggregation, making it compatible predominantly with E/O activations. Regardless of different underlying technologies in experimental demonstrations reported in figure 1, a clear trend can be observed: coherent architectures fall behind the WDM or incoherent schemes by orders of magnitude in compute rates until 2021, operating at 10s of kHz as opposed to 10 GHz achieved by WDM. On the other hand, the speed benefit of WDM architectures is shadowed by their poorer scaling performance owing to the number of required wavelength channels per neuron. The leap in performance of coherent architectures reported by our group in 2021 [30, 31] stems from redesigning the underlying coherent linear neuron, stepping away from the 2 × 2 Mach–Zehnder interferometer (MZI) meshes that were pioneered by Reck et al [34] and further advanced by Clements et al [35], toward 1-to-1 weight mapping via the optical linear algebraic unit (OLAU) [36, 37]. Although employing MZI meshes as core units in optical processors does not imply any fundamental physical limit on the achievable compute rates, it comes with many practical challenges that impose strict requirements on the underlying photonic platform, effectively resulting in 10s of kHz performance with the present-day technologies. Two challenges in particular restrict the practically achievable compute rates, as elaborated in [37]: (i) sharp overall insertion loss (IL) increase with the mesh size and IL per node, degrading the signal-to-noise ratio (SNR) at the output, and (ii) non-restorable loss- and phase-induced fidelity degradation. To remedy the two, high precision phase shifters and ultra-low-loss node technologies are mandatory, which limits the modulation bandwidth, especially if high bit-resolutions are targeted. Owing to the excellent IL tolerance and restorable fidelity, the OLAU allows bypassing the low-IL weighting node constraints typical for MZI-mesh design and supports a whole new library of devices that can operate in 10s of GHz regime without being affected by the associated IL penalty.
Figure 1. Compute rate per axon of WDM (orange circles) and coherent (blue triangles) neuromorphic architectures demonstrated experimentally within the last 6 years [18–31] and the pathway (green square) to the possible performance of the combination of the two.
Download figure:
Standard image High-resolution imageCoherent and incoherent neuromorphic photonic layouts have progressed rather independently so far, failing to incorporate WDM as a speed acceleration factor as has been typically the case in traditional optical systems. Expanding the single-neuron single-wavelength OLAU toward multi-neuron layouts that can also support WDM operation can open completely new parallelization perspectives and pave the road toward TMAC/sec/axon compute rates, indicated by the green bullet in figure 1. The WDM-enabling credentials of the OLAU have been already highlighted in our recent work on multichannel coherent photonic neurons [38], where the combined use of WDM with an OLAU and simple optical switching elements has been shown to create a unique programmable photonic neural network (PNN) setup, where the same hardware can be used for fully-connected, convolutional or multi-neuron NN layers. This work has demonstrated that wavelength dependence of the underlying photonic components plays marginal role as long as amplitude and phase matching is done in the bias branch, theoretically limiting the number of employed optical channels to the ratio of the bandwidth of the de/multiplexers (DE/MUXes) and channel spacing.
At the same time, extending the single-wavelength OLAU toward a photonic Xbar configuration has been verified to support more than one neuron [37], similar to the functionality sustained by analog electronic Xbars. Photonic Xbar layout has been mathematically validated to support 1-to-1 weight mapping over an entire weight matrix, retaining the WDM-compatible credentials of the elementary OLAU setup. In parallel, it exhibits a linear overall IL dependence on the losses of its individual weight node technology, enabling in this way both loss-optimized designs, as well as higher modulation speed weighting blocks. Finally, this Xbar layout allows for loss-induced fidelity restoration, providing a unique advantage among state-of-the-art universal linear optical circuitry in perfectly transferring the targeted matrix into the optical experimental domain.
In terms of analogue processor scaling, the two approaches—singular value decomposition (SVD) and Xbar—are comparable. Assuming sub-dB node modulation technology and a maximum allowed IL of 50 dB along the optical path, SVD could scale up to 16 × 16, given that a value dependent loss (VDL) penalty of 6 dB is expected and assuming that fidelity of 0.8 can be tolerated in training algorithms [37]. Going a step further and assuming an ultra-low-noise photodetector (<1 pA/√Hz) opens a possibility to target sizes up to 32 × 32. Transitioning to the digital domain might be more forgiving in terms of fidelity but imposes strict requirements on SNR as the bit resolution increases. Assuming 4 bit operation, an SNR of >26 dB for symbol-error-rate below 10−3 is required [39], which allows processor sizes of up to 16 × 16 for >10 dBm input optical signal. Xbar offers an advantage in terms of overall IL, which stays below 30 dB even for 64 × 64 matrix and 2 dB per node loss [37]. Its VDL penalty, however, can surpass 20 dB for sizes beyond 16 and random inputs and weights. This penalty is reduced during the training procedure, allowing the processor to reach up to 32 × 32 size with 4 bit resolution and full loss-induced fidelity restoration if the compute rates are of the order of 10G. Moving toward 50G operation or 5 bit resolution restricts the size to 16 × 16.
Merging the two extensions of the OLAU toward supporting (i) multiple channels and WDM operation, as evidenced in [38] to allow for programmability in PNNs, and (ii) multiple spatially separated neurons within a photonic Xbar [37], which effectively transform the OLAU into a universal linear optical operator, can introduce a new performance era for programmable neuromorphic photonics. Having high speed input modulation, matmul at the time of flight, a single step weight programming and at the same time a universal linear optical operator enriched by WDM parallel operation, positions the photonic Xbar as an architecture of choice for matrix-by-matrix and vector-by-tensor multiplication, as we show in section 2. In section 3, we highlight its benefits when employed in neuromorphic photonic circuit applications by using its single column as an NN layer and implementing a fully-convolutional NN (FCNN) in photonics domain, performing the MNIST parity classification with an accuracy degraded by only 2% comparing to the respective value accomplished when executed in software. In section 4, we break down the influence of individual components to the overall FCNN accuracy and conclude to source, modulator and detector operating conditions, which safeguard the accuracy. Finally, in section 5 we draw the conclusions of our study.
2. WDM enhanced photonic crossbar: ultra-high fidelity programmable matmul engine
Coherent linear optics has been brought to the spotlight in recent years in a race to develop a universal multiport interferometer, suited for any real and/or complex vector or matrix representation in photonic domain [16, 18–20, 23, 30, 31, 34–38, 40]. Such a linear engine should allow for vector dot-product or vector-by-matrix multiplication in photonic domain and could find applications anywhere from neuromorphic to quantum photonics. Majority of the research done so far relies on matrix representation via SVD and implements the constituent unitary matrices via 2 × 2 MZI meshes, following the proof that these can be used as unit cells for experimental realization of any discrete unitary operator [34]. Whether in triangular [34], rectangular [35] or diamond arrangement [40], they all suffer from two major drawbacks that have constrained coherent neuron operation to 10 kHz range, as shown in figure 1. Traversing multiple stages of cascaded MZIs leads to IL build-up, scaling linearly with the matrix size for the shortest path and following a square low for the longest one. More importantly, on its journey from the input to the output, the signal takes multiple paths, effectively 'seeing' different losses, interfering along the way with other signals that had also traveled along the various paths. Even if ideal phase control in and out of the MZI is assumed, fidelity is irreversibly degraded due to multi-path propagation as long as MZI IL is nonzero, which leads to strict requirements for ultra-low-loss node technologies and ultra-stable phase control.
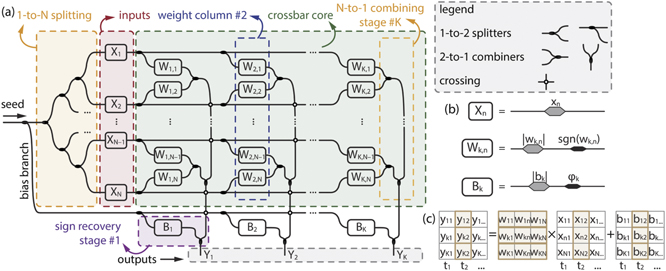
In order to ensure that each signal passes a unique path and encounters identical loss penalties, we step away from SVD matrix implementation and introduce 1-to-1 weight mapping via the dual-IQ based OLAU, arranged in a 2D spatial matrix as figures 2(a) and (b) reveal [37]. Its loss-balanced layout can safeguard the fidelity and opens the possibility to use modulators with the bandwidths of 10s of GHz. As figure 1 shows, such approach increases compute rate per axon of coherent prototypes by orders of magnitude, allowing them to compete with WDM-based solutions, while retaining the same functionality of vector-by-matrix multiplication at a single wavelength, figure 2(c). Moreover, Xbar does not require preprocessing of the weights that will be applied, as is the case with MZI-mesh based solutions, which call for SVD followed by unitary matrix factorization [35]. This makes impairments easier to detect and prevents their spread over multiple matrix elements. Finally, in an effort to avoid coherent detection schemes, we introduce a bias branch
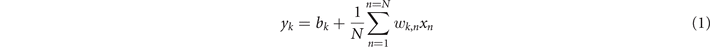
which aids in conversion of sign information from the phase of electrical field to its magnitude, making Xbars equally easy to combine with all-optical or E/O activation units (AUs). In (1), k ∈ [1, K] and n ∈ [1, N] denote the column and row indices, respectively, xn is the nth element of the input vector, wk,n is the (k, n) element of the weight matrix, bk is the kth element of the bias vector and yk is the kth element of the output vector. The vector/matrix dimensions are spatial in character (N input, row waveguides and K output, column waveguides), implying that in one temporal instance ti, one input vector can be processed by being multiplied by a single weight matrix to yield a single output vector.
Figure 2. (a) Schematic representation of N × K photonic crossbar, including the OLAU and the bias branch. The OLAU consists of 1-to-N splitting stage, a column of N inputs, matrix of N × K weights and the combining stage. The sign recovery stage gives the outputs Yk . (b) Equivalent circuits of the input, weight and bias module in case of single-channel Xbar and (c) the corresponding representation of vector-by-matrix multiplication.
Download figure:
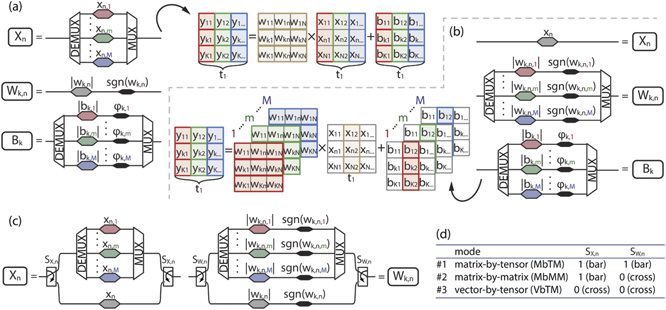
Standard image High-resolution imageStriving to use the full potential of photonic platform and further boost the throughput, we resort to WDM for extending the capabilities of the Xbar beyond one output vector at a time. In our recent work on WDM enhanced programmable photonic neurons [38], we introduce a concept of input or weight sharing by replacing some of the modulators by more elaborate modulator banks, enclosed between DEMUX/MUX pairs. In this manner, parallel operation of convolutional or fully-connected NN layers can be achieved with substantial power savings and marginal IL penalty by making use of spectral dimension. In other words, in a single temporal instant, a whole matrix of inputs can be processed by extending one of its dimensions along the space (different input waveguides), and the other dimension along the spectral domain (different optical channels), as indicated in figure 3(a), or, alternatively, weight tensor can be implemented by representing its two dimensions in space (row and column waveguides) and the third dimension in spectral domain (each channel 'sees' different weight matrix), as represented in figure 3(b). Moreover, we show that the impairments coming from the wavelength dependent component performance can be easily counteracted within the bias branch modulator banks.
Figure 3. WDM enhanced Xbar in (a) shared weight configuration and the resulting matrix-to-matrix multiplication and (b) shared input configuration and the resulting vector-by-tensor n-mode multiplication operation. Modulator banks support M optical channels, yielding a throughput proportional to M × N × K. (c) Upgraded, programmable input and weight banks enclosed between pairs of dedicated optical switches enabling a unique hardware which performs both MbMM shown in (a) and VbTM shown in (b), as well as matrix-by-tensor n-mode multiplication (MbTM) according to the switch states listed in table (d).
Download figure:
Standard image High-resolution imageTransferring the modulator and/or weight bank principle into the photonic Xbar leads to a WDM boosted universal linear operator that allows for a multifunctional multi-neuron layout. Replacing the input modulators by modulator banks and leaving the Xbar core as it was, as shown in figure 3(a), allows for parallel processing of multiple columns of the input matrix simultaneously (at temporal instant ti), effectively achieving matrix-by-matrix multiplication (MbMM):
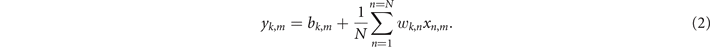
In (2), k ∈ [1, K], n ∈ [1, N] and m ∈ [1, M] denote the column, row and channel indices, respectively, xn,m is the nth element of the input vector at mth wavelength, wk,n is the (k, n) element of the weight matrix, which is colorless (all channels pass through the modulators in multiplexed form), bk,m is the kth element of the bias vector at mth wavelength and yk,m is the kth element of the output vector at mth wavelength. Imprinting of the input/bias in a wavelength selective manner is achieved by demultiplexing the signal prior to modulating each of the channels and later multiplexing them together within the modulator bank. The dimensions n and k are spatial in character (N input waveguides and K output waveguides), whereas dimension m represent the spectrum with M channels. This implies that input and bias matrices have mixed domains (space and spectrum), while weight matrix relies solely on 2D space. This mode of operation resembles convolution since each input column-vector (all inputs of the same 'color') gets filtered by the same weight matrix kernel.
On the contrary, leaving the input stage as is and replacing each weight node by a weight modulator bank, figure 3(b), results in vector-by-tensor multiplication (VbTM) [41]:
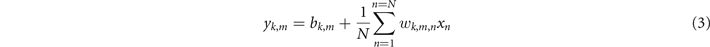
where k ∈ [1, K], n ∈ [1, N] and m ∈ [1, M] denote the column, row and channel indices, respectively, xn is the nth element of the input vector, which is colorless (all channels pass through the modulators in multiplexed form), wk,m,n is the (k, n) element of the weight matrix at mth wavelength, or, equivalently (k, m, n) element of the weight tensor, bk,m is the kth element of the bias vector at mth wavelength and yk,m is the kth element of the output vector at mth wavelength. As in previous case, imprinting the values in a wavelength selective manner relies on DE/MUX enclosed bank of single-channel modulators. The dimensions n and k are spatial in character (N row waveguides and K column waveguides), whereas dimension m represent the spectrum with M channels. Input vectors remain defined only in spatial domain, whereas weights and biases use a mixture, producing a weight tensor (2D space with spectrum) and a bias matrix (space and spectrum). Described operation resembles a fully-connected layer, where, in a single temporal instant ti, the input column vector 'sees' different matrix slices of the weight tensor, each of a different 'color', indexed by m, mapping them to the unique column of the output matrix {yk }m .
Both operations, MbMM and VbTM, are essential for high load AI models [42]. The two different MbMM and VbTM operational modes can be also offered by a single hardware setup by simply incorporating reconfigurability through optical switching elements, as shown in figure 3(c). In this layout, the input stage comprises a modulator bank branch (as in figure 3(a)) and an additional single optical modulator branch (as in figure 3(b)), with the choice of the desired path controlled via the optical switches encircling the modulators. The weighting stage follows the same principle, and it consists of a weight bank branch (as in figure 3(b)) and a single weight module branch (as in figure 3(a)), again forming the two discrete connectivity arms between the two switches. Depending on the configuration of the switches, tabulated in figure 3(d), multiple modes of operation are supported. Setting the two optical switches at the input stage to the bar state forces the WDM optical continuous wave (CW) beams to enter the modulator bank, while operation of the two optical switches at the weighting stage at their cross state directs the modulated WDM stream to the common weighting module. This configuration effectively implements MbMM, the same functionality supported by figure 3(a). The functionality revealed by figure 3(b), VbTM, can be facilitated by forcing the input stage switches to operate in their cross state and the weighting stage switches in their bar state, so that the WDM CW streams get modulated by the same input signal but later enter the weight bank to have every channel multiplied by a different weight value.
Translating the aforementioned concept to the PIC requires a choice of appropriate node technology, which will depend on targeted application. The constrains for input and weight modulators are significantly more relaxed comparing to the ultra-low-loss MZIs needed in unitary and SVD architectures, as analyzed in detail in [37]. Inputs are typically expected to operate at high data rates, making the high bandwidth E/O modulation preferable, whereas the weights typically remain fixed in the feed-forward (FF) inference application, allowing for low-IL thermo-optic (T/O) [30, 43] or phase change material non-volatile optical memory technology to be exploited [28, 44, 45]. Compared to the single-wavelength photonic Xbar layout analyzed in [37], the additional losses experienced by a WDM empowered Xbar design account only the IL of an individual MUX/DEMUX pair, which can be assumed to have a typical value of 1.5 dB per device that is currently supported by silicon-on-insulator photonic fabrication technology [46–48].
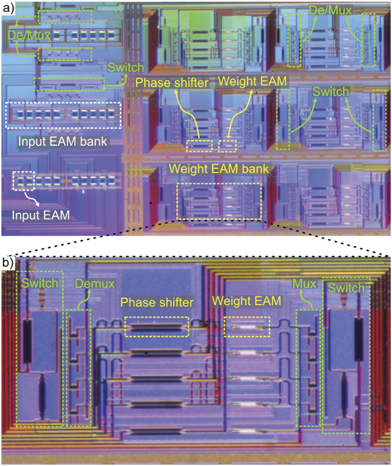
Figure 4(a) depicts a microscope image of the first programmable 4 × 4 PNN chip, which has been recently fabricated in silicon using Si–Ge electro-absorption modulator (EAM) technology both for its input and weighting stage. This chip forms an extension of the silicon coherent linear neuron prototype employed recently in MNIST classification experiments with a record-high compute rate of 32 GMAC/sec/axon [31], enriched with WDM-enabling modules at both its input and weighting stage, according to the principles from figure 3(c), and at the same time expanded into a 4 × 4 Xbar setup. Figure 4(b) shows a zoom-in of the programmable four-channel weighting stage, where EAMs are used for the absolute weight value and T/O silicon phase shifters (PSs) for weight sign imprinting, with 0/π signifying a positive/negative weight sign. Moreover, the switches embracing the weight bank allow the choice between a common weight and a channel-wise weighting, seamlessly supporting switching between MbMM and VbTM operation. Finally, the use of EAMs in weighting stage of the Xbar supports in situ training by guaranteeing the same, >10 GHz update rate for both inputs and weights.
Figure 4. (a) Microscope image of the programmable photonic Xbar exploiting Si–Ge EAMs at both input and weight banks, supplemented by T/O phase-shifters for sign imprinting, embraced by DE/MUXes and configured by the switches. (b) Zoom into one node of the Xbar, detailing the weight bank and programmability features.
Download figure:
Standard image High-resolution image3. Photonic fully-convolutional neural network
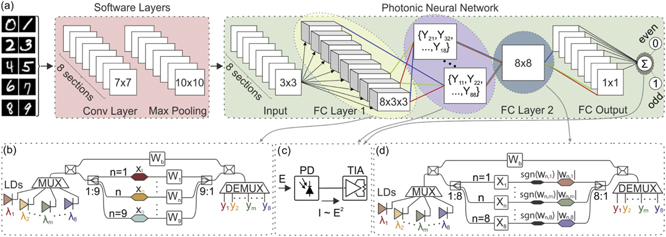
Stepping away from matrix-by-matrix and vector-by-tensor multiplication functionality offered by WDM enhanced Xbar, figure 3, from this point on, we restrict our analysis to its single column, still operating with multiple channels, showcasing that even under these circumstances, a challenging, multi-layer photonic NN can be implemented with an excellent accuracy, approaching the limit set by software training. For our case-study, we choose an image recognition task from a widely used MNIST benchmark dataset [49, 50] and classify the 28 × 28-pixel hand-written digits {0, ..., 9} according to their parity using a hybrid software-photonic FCNN. The FCNN, schematically shown in figure 5(a), consists of two stages, where the first stage comprises two initial software layers that are used for extracting a two-dimensional 3 × 3 feature map with eight channels, serving as an input to the second stage. Feature extraction in the first stage is done by an 8-filter 7 × 7 kernel size convolutional layer with an associated bias, followed by a max pooling layer with kernel size 10 × 10 and a stride of 6. The resulting input tensor, defined on the domain 8×3×3, is reformatted to an 8 × 9 matrix and passed to the second stage of the FCNN that is implemented via a PNN and performs digit parity identification, outputting 0 if the digit is even and 1 if it is odd.
Figure 5. (a) Schematic representation of the hybrid software-photonic FCNN with the pink shaded area denoting software layers and the green one PNN layers. (b)–(d) Building blocks of a single section of the (b) 1st and (d) 2nd photonic layer, with (c) O/E/O activation function located at the output of each layer. (b) and (d) Colored hexagons represent amplitude modulators (E/O MZMs for input, T/O MZMs for weights), black hexagons represent phase modulators (T/O for weights) and white boxes labeled by X and W stand for input and weight modulator banks, a look into which is given in figures 3(a) and (b), respectively.
Download figure:
Standard image High-resolution image3.1. Photonic NN topology
Traditionally, convolutional layer is implemented by performing either convolution or cross-correlation operation of the input with a kernel aiming to extract the feature map, which is passed through the nonlinearity, denoted as the activation function [51]. Typically, a classification layer follows, giving a label prediction. On the contrary, when employing photonics, accompanying limitations and constrains arising from the hardware platform itself demand restructuring of the FCNN layers to achieve the same functionality to that of a software.
In the green shaded area of figure 5(a), we schematically show the PNN, composed of two linear layers, each of them followed by an O/E/O nonlinear activation, implemented by a PD and a transimpedance amplifier (TIA), figure 5(c). The nonlinearity perceived by the first photonic layer corresponds to the sine of a squared output, since the TIA output is used for driving the input Mach–Zehnder modulator (MZM) of the subsequent layer incorporating in this way also the MZM transfer function nonlinearity. At the output of the second layer, the nonlinearity is a simple square function, representing the transformation of the electrical field magnitude to the optical power recorded by the PD as figure 5(c) reveals. Both linear layers rely on building blocks which correspond to a single column of a WDM enhanced Xbar, shown in detail in figures 5(b) and (d), with a distinction that the weight banks are used in the first layer (VbTM mode, figure 3(b)) and input banks in the second one (MbMM mode, figure 3(a)). In both cases, the layers are supplied by the multi-channel (M = 8) multiplexed CW optical signal originating either from an array of independent laser diodes (LDs) or, alternatively, from an optical frequency comb.
The first photonic layer is organized in K = 8 sections, each with N = 9 inputs, amounting to the dimension of the reformatted 8 × 9 input feature matrix. A single, kth section, detailed in figure 5(b), accepts an N-element input vector Xk = [xk,1, ..., xk,N ]T, with a single element xk,n , 1 ⩽ n ⩽ N, which is pondered by a wavelength-selective M × N matrix of weights via the weight banks, Wk = [wk,1,1, ..., wk,1,N ; ...; wk,M,1, ..., wk,M,N ], with M = 8 corresponding to the number of employed wavelengths and consequently, the number of outputs from each section. Each output also includes a bias term, imposed via the M-element bias branch vector, Bk = [bk,1, ..., bk,M ]T. Finally, the mth output of the kth section can be determined as
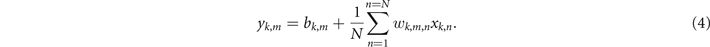
Accounting for the layer depth of eight sections, (4) reveals matrix (X ∈ 8×9) by tensor (W ∈
8×8×9) n-mode product operation [41], yielding a new matrix (Y ∈
8×8) as an output.
The output of the first photonic linear layer is sent to the array of photodetectors, each comprising a PD and a TIA, as figure 5(c) shows. The role of O/E/O conversion is multiple: it serves as an interface between the two photonic layers by generating an electrical signal that drives the following layer's input modulators, but it also implements a nonlinear activation function together with the transfer function of the second layer's input modulator, by converting the electrical field of the optical signal to the photocurrent proportional to the optical power, i.e., applying a square nonlinearity, which is then mapped to the optical signal via the sine transfer function of the MZM modulator. Figure 5(a) reveals that each AU block takes as an input a single, distinct channel from each section of the first layer in a cyclical manner and forwards them as an input to the next layer's branch. Mathematically, the transformation can be described as a double circulant-shift, first shifting the kth row of the output by k − 1 to the left, and then down-shifting the mth column of the output by m − 1, yielding the input matrix into the second layer:
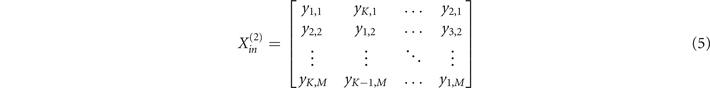
where yk,m stands for the output of the kth section at mth wavelength.
Shuffling the wavelengths between the two layers enables us to apply fast matrix multiplication and backpropagation on GPU during software training since this operation is already supported by most DL frameworks, but also opens the possibility for employing all-optical activations, such as the SOA-based sigmoid [52] or the injection-locking based ones [53]. It should be noted that, in this case, a minor modification of the second layer is needed, which involves removing the 1-to-8 splitting stage and making use of the existing weight PSs not only to imprint the sign of the weight, but also to regulate per-branch phase accumulation which would guarantee the appropriate phase difference between the optical signals such that they interfere constructively at the combining stage. Input modulators can be either omitted or set to operate in transparency regime. On the other hand, if training is done knowing in advance that no optical AUs will be used, the restrictions related to the output shuffling can be eased.
Returning to the O/E/O activation case, which is shown in figure 5, we recall that the output of the first photonic layer was an 8 × 8 matrix, now used as an input to the second photonic layer distributed over eight branches and eight wavelength channels using input modulator banks, as shown in figure 5(d). To achieve classification function, this matrix is filtered by a single 8 × 1 kernel of weights, yielding an 8 × 1 output vector, with each vector element carried by a distinct wavelength. The final step assumes joint accumulation of the output channels via a single PD, yielding a prediction label on whether a digit is even (outputs '0') or odd (outputs '1') in a similar manner as typical binary on–off keying optical communication channels resolve the bits 0 and 1. This method allows us to determine the accuracy of the FCNN both by error counting, but also relying on well-known bit-error-ratio (BER) measurement, calculated from the probability density distributions using the target labels.
3.2. Training and implementation
The network was trained in a software manner on the MNIST dataset, which includes 60.000 training samples and 10.000 testing samples. More specifically, the network is optimized for 100 epochs using RMSprop optimization algorithm [54] with learning rate set to 0.0001 and mini-batch size equal to 32.
Although physical properties of the underlying photonics hardware, such as limited resolution, noise, extinction ratio or bandwidth limitation, were not accounted during the software training, constrains were imposed to the ranges of values of inputs and parameters (weights and biases). More precisely, the inputs were bounded to [0, 1], the weights to [−1, 1], whereas the biases were restricted to [−1, 1], such that sign integrity of the output field is guaranteed. To compensate the effects of such constraints we apply regularization terms to the employed binary cross entropy loss to exploit the intrinsic ability of NNs to accumulate such limitations through backpropagation. To this end, the network is optimized to eliminate values that cannot be applied during the hardware inference using the following loss function:
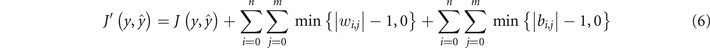
where  denotes the binary cross-entropy loss, y and
denotes the binary cross-entropy loss, y and  are the targets and predicted values respectively, while m is the number of neurons in ith photonic layer.
are the targets and predicted values respectively, while m is the number of neurons in ith photonic layer.
The PyTorch [55] DL learning framework is used to offline train the networks and the photonic network itself is later deployed in VPIphotonics Design Suite (VPI) environment [56], achieving, respectively, 95.9% and 95.8% evaluation accuracy, highlighting the benefits of such co-simulation design.
4. Results and discussion
Performance evaluation of the FCNN through physical layer simulation in VPI environment is organized in five stages: (i) loading of the parameters obtained by software training, namely, input matrices fed into the first photonic layer, target labels for accuracy estimation after the second layer, as well as weights and biases for both photonic layers; (ii) physical implementation of the first photonic layer; (iii) inter-layer activation and channel shuffling stage; (iv) physical implementation of the second photonic layer followed by an AU; (v) performance evaluation and error detection stage. Input CW seed signal for each of the layers is generated via a designated laser bank, consisting of M = 8 LDs centered at the 100 GHz C-band DWDM grid, covering the range [194.0, 194.7] THz. We note here that the WDM-enhanced Xbar as a whole, as well as its exemplary FCNN implementation, is compatible with arbitrary wavelength range, including O-band. The performance will ultimately depend on the performance of individual photonic components, both passive (waveguides, splitters/combiners, DE/MUXes) and active (laser source(s), amplitude and phase modulators, photodetectors). Having photonic technology mature in both bands guarantees good performance per channel. Lasers are nominally emitting 19 dBm of optical power in the first and 10 dBm in the second laser bank. Having the first bank supplying eight sections, as opposed to the second bank which supplies only one, figure 5(a), raises a penalty of 9 dB in the first case, which brings the CW seed signals at the same power level of 10 dBm at the input of each section, be it in the first or the second layer.
Input, weight, and bias values coming from software training are mapped from the domains outlined in section 3.2 to the appropriate voltages using analog-to-digital converter with finite bit resolution. As shown in figures 5(b) and (d), photonic layers are operating in different regimes, first one having common inputs and wavelength selective weights, and the second one vice versa. Inputs are imprinted using E/O MZMs with finite extinction ratio (ER) and IL. We assume that the MZM driver's transfer function can be approximated by the low-pass Bessel filter of the 1st order, consequently imposing restriction on the input signal bandwidth, resulting in finite raise and fall times. Demonstrating inference application allows for T/O MZMs and PSs to be used as weights, both of which have finite IL, and the former also finite ER. We assume all modulators are realized in Si technology and exhibit wavelength dependent behavior when shared among multiple channels. This effect is compensated by PSs in the bias branch, as detailed in [38]. Moreover, we introduce an additional variable optical attenuator in the bias branch which matches the excess attenuation seen by the signal in the OLAU and guarantees the appropriate bias signal level for conversion of the sign from the phase to the field magnitude. For signal multiplexing and demultiplexing arrayed waveguide gratings are used with finite IL and crosstalk (CT). To account for additional noise sources not captured by the existing components, we include a variable optical signal to noise ratio (OSNR) module, allowing us to increase the content of the noise in the system in a controllable manner.
The same AU is used after both photonic layers, as shown in figure 5(c), including a PD of the responsivity 1 A/W followed by a TIA, both of which have finite bandwidth, modeled by a low-pass Bessel filter of the 1st order. The nominal impedance of the TIA is 400 Ω in the absence of IL of the employed photonic components throughout the setup. When finite IL exists, impedance increases proportionally to compensate accumulated losses and guarantee the required voltage range at the input of the second photonic layer.
Finally, after the detection stage, symbol error probability is measured to determine the FCNN accuracy. Two approaches are adopted, namely, error counting and BER estimation based on the probability density distributions of the two output labels—0 and 1. The second approach allows to estimate the expected error when a longer test sequence is used then the one provided by the MNIST dataset.
In all simulation runs the data rate is set to 10 GBd with 256 samples/symbol, guaranteeing that all impairments will be captured in the resulting waveform. We note that such high sampling rate is selected only to mimic the analog nature of the signal that exists in practice, while the sampling at the detector side would require no more than two samples per symbol to resolve the amplitude. The parameters used in the simulations are included in table 1.
Table 1. Simulation parameters for ideal, optimistic and realistic case
| Parameter | Unit | Ideal | Optimistic | Realistic |
|---|---|---|---|---|
| X bit res. | 64 | 8 | 4 | |
| X MZM ER | dB | 30 | 20 | 8 |
| X MZM IL | dB | 0 | 4 | 4 |
| X MZM BW | GHz | 20 | 8 | 8 |
| W bit res. | 64 | 8 | 3 | |
| W MZM ER | dB | 30 | 20 | 12 |
| W MZM IL | dB | 0 | 1 | 1 |
| W PS IL | dB | 0 | 1 | 1 |
| DE/MUX IL | dB | 0 | 1.5 | 1.5 |
| DE/MUX CT | dB | 70 | 30 | 20 |
| PD dark current | nA | 0 | 40 | 40 |
| PD BW | GHz | 20 | 8 | 8 |
| TIA noise | pA/Hz1/2 | 0 | 20 | 20 |
| TIA BW | GHz | 20 | 8 | 8 |
| OSNR | dB | 300 | 30 | 25 |
aAbbreviations: X: input, W: weight, MZM: Mach–Zehnder modulator, PS: phase shifter, bit res.: bit resolution, ER: extinction ratio, IL: insertion loss, BW: bandwidth, DE/MUX: de/multiplexer, CT: crosstalk, PD: photodiode, TIA: transimpedance amplifier, OSNR: optical signal-to-noise ratio. bLimited by the floating-point number representation.
The network testing was carried out for three different physical layer specification sets, with the two first sets having the role of defining the baseline framework and the third set evaluating the network performance under realistic conditions. Initially the system was tested under almost ideal physical layer conditions in order to evaluate the system's performance in comparison to the results obtained when executed entirely in the software domain. The corresponding physical layer parameter value-set is summarized under the ideal column of table 1. As a next step, two different cases were studied where multiple limitations were gradually introduced in the network, representing more realistic systems. The respective physical layer parameter values are presented in the last two columns of table 1, named as optimistic and realistic. The main difference between the optimistic and realistic cases concerns the assumption of improved operational settings with respect to input and weight bit resolution, ER, DE/MUX CT and OSNR penalty in the optimistic case, which may be eventually feasible only through additional advances in PIC fabrication platforms. On the contrary, the realistic case takes into account respective parameter values that have been already accomplished by state-of-the-art silicon photonic fabrication platforms, offering in this way an indication of its practical perspectives even within the current technological framework.
4.1. Results on parity identification in MNIST dataset
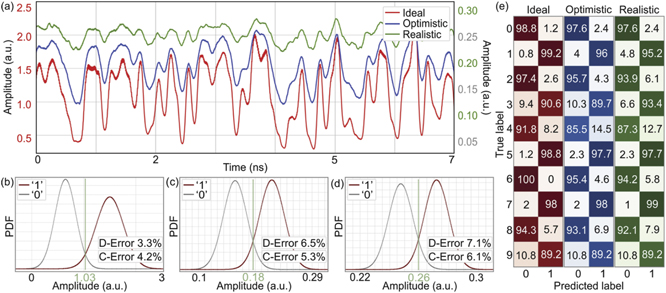
Figure 6 shows the results for the three analyzed cases with the parameters reported in table 1. Looking at the waveforms at the output of the second layer reported in figure 6(a), a very good agreement between the three cases can be observed, even though the degradation occurs when moving from the ideal to the realistic case, as expected. Introducing the cumulative IL penalty of 12 dB in optimistic and realistic case brings the signal amplitude down by approximately an order of magnitude in comparison to the ideal one, whereas the finite ER of the input and weight modulators reduces the signal's modulation depth. The combined influence of finite ER, bandwidth, and low bit resolution, makes some of the amplitude levels indistinguishable, as can be observed in the range of [2.8, 3.1] ns and [3.6, 3.9] ns. However, the overall shape of the waveform is well preserved even under realistic circumstances.
Figure 6. (a) Waveforms of the signals leaving the second photonic layer for the ideal (left-hand axis) and optimistic and realistic set of parameters (right-hand axis). (b)–(d) Probability density distributions for the labels '0' and '1', together with the decision threshold and the respective errors (D—distribution, C—counting) for (b) ideal, (c) optimistic and (d) realistic case. (e) Confusion matrixes for three analyzed cases demonstrating the probability of correct vs erroneous digit classification according to parity.
Download figure:
Standard image High-resolution imageProbability density distributions reported in figures 6(b)–(d) agree with the waveforms from figure 6(a), revealing that the Gaussians describing the two levels, 0 for even and 1 for odd, remain well defined for all three cases, although the overlap increases going from ideal, figure 6(b), to realistic case, figure 6(d), as anticipated. The reduction in amplitude, as well as the modulation depth, is also observed in figures 6(b)–(d), but probability density distributions still leave enough room for a threshold to be established yielding the error probabilities of [3.3, 6.5, 7.1]% for the three cases. Comparing to the errors determined by counting, [4.2, 5.3, 6.1]%, the trend is well captured and can be reliably used for estimating the FCNN performance for a longer test sequence. Standard deviation of the label 1 is somewhat larger than the one corresponding to label 0 in ideal case, even though they are comparable. This asymmetry vanishes moving toward optimistic and realistic cases, implying that the noise and nonlinearities distribute evenly between the two labels.
To get a better, per-digit parity prediction overview, we report the confusion matrix in figure 6(e) for all three analyzed cases, revealing the percentage of true/false label prediction. We note that digits did not have the same frequency of appearing, so the errors reported in figure 6(e) do not enter with the same weight in the overall error reported in figures 6(b)–(d). Nevertheless, figure 6(e) still gives an indication where the improvement can be done for future FCNN implementations. It can be observed that some digits are universally easy for classification (e.g., 0 and 7), whereas some remain challenging even in the ideal case (e.g., 3, 4 and 9). The error typically increases when moving from ideal to any of the other two cases, with a very few exceptions (3, 7) that can be attributed to the test sequence not being long enough.
4.2. Network performance analysis
To better understand the origin of performance degradation in realistic case as opposed to the optimistic one, we study individual contributions of some common imperfections and/or penalties seen by the optical signal in the PNN, choosing BER as a figure of merit. In what follows, unless otherwise stated, all parameters in the physical implementation of the FCNN are set to optimistic values from table 1.
Figure 7(a) shows BER dependence on IL penalty introduced in the system immediately following the laser banks. We study three different cases, where the loss is imposed to the input signal for each of the layers individually (first—L1; second—L2) and both combined (L1 + L2). Results reveal L1 is more resilient than L2, offering a margin of 4 dB for the same error of 7% and approximately 3 dB for the error of 8%. This can be attributed to the modulation loss which is accumulated as we traverse from one layer to another and to the change in the input value probability distribution between the two layers. Assuming initial inputs to the first photonic layer and parameters of both layers (weights and biases) are uniformly distributed on their respective ranges introduces a 3 dB-penalty per amplitude modulator, accumulating to approximately 6 dB at the output of the L1. More importantly, the sum of the products of uniformly distributed quantities on the ranges specified in section 3.2 approaches to Gaussian probability distribution at the first layer's output, which acts as a penalty to the modulation depth of the second layer's input, since majority of the values will be clustered around the distribution's mean. Unlike the modulation loss penalty which may be counteracted by TIAs to a certain degree, the change in distribution will remain. Such penalty reflects adversely on the final BER, requiring higher PD sensitivities in the second layer, or, alternatively, sufficient optical power to resolve the levels of 0 and 1. When IL is introduced in both layers, a cumulative effect can be observed, implying that the errors in two layers are uncorrelated, which is expected since the weight and bias values are imposed independently.
Figure 7. FCNN error rate versus (a) IL penalty introduced in layer 1 (L1), layer 2 (L2) and both layers (L1 + L2), (b) ER for input (E/O) and weight (T/O) modulators, (c) TIA's thermal noise for two CW input optical powers, 10 and 2 dBm, and (d) bit resolution of inputs and weights.
Download figure:
Standard image High-resolution imageReducing the ER below 10 dB raises the BER by 0.5%, from 6.5 to 7% as figure 7(b) reveals, regardless of the modulator in question—input or weight. Both act similarly in terms of error penalty. Nevertheless, from a practical standpoint, input modulator is somewhat more critical since high-speed modulators, such as EAM, may not currently be able to support ERs beyond 8 dB, limiting the performance of the PNN.
Introducing the TIA noise at the detection stage, figure 7(c), plays marginal role as long as the optical power reaching the PNN is high enough, which is also confirmed by the smooth waveforms shown in figure 6(a). Reducing the laser power reveals the increase in error penalty coming from TIA noise.
Finally, we explore the impact that limited bit-resolution of the driving signal has on BER. Figure 7(d) shows that both weights and inputs can be driven with no more than 4 bits without the loss in accuracy, complying with the commonly quoted guideline for PNN implementation, which additionally relaxes energy and area requirements [33]. Reducing the weight amplitude resolution even to 2 bits still yields excellent results, which is in agreement with the trend of low-precision training algorithms [6]. However, the inputs prove to be more sensitive, which can be attributed to the effective reduction in the modulation depth due to probability distribution transformation from the first to the second layer, imposing stricter requirements for resolving two close analog levels.
It is worth noting that many of the limitations encountered in the PNN can be eventually alleviated by enforcing a hardware-aware DL training framework where the training algorithm incorporates the physical layer limitations of the underlying photonic hardware a priori in the training process [8, 9]. Accounting for quantization (limited bit resolution) [10, 11], limited ER or bandwidth has already been demonstrated as a viable solution for performance upgrade [8, 9].
5. Conclusions
Aiming to blend the two architectural approaches favored by neuromorphic photonics—WDM (or incoherent) and coherent, we show how wavelength domain can be exploited for achieving parallel operation of the coherent photonic crossbar, relying on 1-to-1 weight matrix mapping pioneered by our group, opening a path toward TMAC/sec/axon performance. Enclosing the input and weight banks between optical switching elements, we introduce programmability feature to our system, offering a single photonic platform that can tackle various matmul operations between the operands of different dimensions, always striving for energy conservation and maximum efficiency for a given task. We demonstrate how such platform can be used in inference task by realizing multilayer PNN and benchmarking its performance against MNIST dataset in digit parity recognition task. Our results show that the accuracy degradation compared to software one is only 2%, without making the training algorithm aware of the underlying photonic hardware. Following a detailed performance study of the FCNN, we identify that 4 bit resolution is sufficient for inputs, whereas the weights can be quantized with as low as 2 bit accuracy without significant degradation in network's performance. Finally, we present the guidelines for modulator specifications in terms of ER, as well as the system as a whole in terms of overall IL that safeguard the high-accuracy performance.
Acknowledgments
The research work was partially supported by the Hellenic Foundation for Research and Innovation (H.F.R.I.) under the 'First Call for H.F.R.I. Research Projects to support Faculty members and Researchers and the procurement of high-cost research equipment grant' (DeepLight, Project Number: 4233).
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.