Abstract
Swarm robots are frequently preferred for the exploration of harsh environments and search and rescue operations. This study explores the factors that influence the movement strategies of autonomous robot swarms and their impact on swarm distribution in the field, employing simulation-based analysis. The research consists of two parts: initially, robots undergo free-fall as passive entities, followed by a phase where they employ predefined movement strategies from their fall positions. The study aims to investigate how the initial position and related parameters affect movement characteristics and the ultimate swarm distribution. To achieve this objective, four parameters-radius, height, mass, and the Coefficient of Restitution-were identified, each assigned three different values. The study observes the effects of these parameters on robot motion, considering motion strategies such as Random Walk, Levy Walk, Markov Process, and Brownian Motion. Results indicate that increasing parameter values induce changes in the position values of the free-falling swarm in the first part, which is the initial position for the second part, influencing movement strategies in diverse ways. The outcomes are analyzed concerning the radial and angular spread of the robots. Radial spread measures how far swarm elements spread from their initial positions, while angular spread indicates how homogeneously the robots are distributed according to the polar angle. The study comprehensively investigates how the movement strategies of autonomous robot swarms are impacted by parameters and how these effects manifest in the results. The findings are anticipated to enhance the effective utilization of autonomous robot swarms in exploration missions.
Export citation and abstract BibTeX RIS
Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Swarm robots are designed to be used for tasks such as field scanning, observation, and substance search, which are complex and often take place in areas where the structures of the terrain are not known in advance or detailed maps are not drawn. To perform these actions properly, the initial positions of the robots are important for swarms that are spreading around. If the swarms scatter well around the released area, the goals can be fulfilled more efficiently. The problem of dispersion in multi-robot systems could be loosely defined as maximizing the sensor coverage area while preserving the connectivity within the swarm.
There are many studies about swarm dispersion and scattering presented in the literature. Naval proposes a common methodology based on electrostatic attraction or repulsion [1]. Simulations were performed for the vision-based dispersal, queueing, and navigation methods proposed above using the ARGoS simulation environment developed to show the effectiveness of the dispersal procedure of swarm bot. In the work presented by Amir and Bruckstein a swarm of asynchronous, autonomous mobile robots completely covering an unknown environment based on the 'totally asymmetric simple exclusion process' in statistical mechanics is considered [2]. The robots behave identically and in case of a crash, they disappear. Their results show that with a simple and local rule of behavior, the unknown environment can be quickly covered while the performance of the swarm degrades as crash density increases. Shah and Vachhani focus on decentralized swarm aggregation, introducing a controller facilitating swarm cohesion without global communication, a pivotal step towards autonomous swarm behavior [3]. Zhu et al address communication limitations by proposing a method for collaborative action using distributed consensus, effectively demonstrated with quadrotors [4]. Zhao et al's self-adaptive algorithms for 3D swarm movement tackle critical challenges such as obstacle avoidance and network connectivity, showcasing significant potential for real-world application [5]. Meanwhile, Petráček et al, and others delve into various aspects of decentralized swarm structures and bio-inspired algorithms, each contributing unique insights into swarm behavior and functionality. Petráček et al used a method that each member of the swarm uses the vision-based UV mutual relative localization of neighboring swarm robots [6]. Cardona et al's method used an algorithm based on ant behaviors which is for robots without direct communication and share information similar to pheromone trails in ants receiving environmental information only from robots entering their vicinity, thus attempting to explore [7]. Tang et al's comprehensive analysis of multi-UAV (unmanned aerial vehicle) collaboration algorithms underscores the complexity and importance of coordination in swarm systems, offering valuable guidance for future research and development [8]. Arnold et al's simulation-based study highlights practical applications of behavior-based swarming algorithms in disaster response scenarios, emphasizing the potential for swarm robotics to make a significant impact in critical situations [9]. Additionally, research in agent-based models by CoppeliaSim elucidates the underlying dynamics of animal swarms, providing valuable insights for designing effective control algorithms for autonomous systems [10]. Furthermore, consensus strategies and user-friendly systems for swarm formations, explored by other researchers, offer practical solutions for optimizing swarm performance and functionality in diverse environments [11]. These collective efforts represent significant strides in swarm robotics, paving the way for enhanced autonomy and efficiency across a wide range of applications. Recent studies have made significant advancements in swarm robotics, drawing inspiration from nature to develop innovative algorithms for various applications. Connor et al introduce FIRA, a fish-inspired robotic algorithm designed to mimic the behavior and communication of schooling fish [12]. Through predictive elements and indirect communication inspired by stigmergy, FIRA demonstrates superior performance in collision avoidance and exploration tasks, establishing its effectiveness in replicating fish behavior in robotics. Xiong et al propose a distributed self-organized Reynolds swarm model for UAVs, leveraging biological swarm behavior to achieve compact and ordered collective motion in cluttered environments [13]. In their paper, researchers introduce a user-friendly system for efficiently arranging UAVs in a swarm formation, crucial for establishing a temporary communication network useful in search and rescue missions. The proposed system utilizes an iterative genetic algorithm to generate optimal layouts, providing easy-to-comprehend visualizations and outperforming the k-means clustering algorithm [14]. Additionally, Mir et al present MAE-PAO, a hybrid approach combining deterministic Multi-Agent Exploration with a parameterized Aquila Optimizer for Multi-Agent Space Exploration [15]. Through stochastic elements and comparative simulations, MAE-PAO demonstrates enhanced map exploration with lower execution times, offering promising prospects for efficient multi-agent robotics operations. In another paper, researchers used an algorithm to make a consensus between sub-swarm groups of a large swarm to detect the victim in an environment [16]. This study claims that the sub-swarm formation strategy is effective for detection, navigation, and obstacle avoidance. Bayert and Khorbotly present a method for the dispersion of swarm robots that uses the received signal strength of the radio signals and the gradient descent algorithm for efficient dispersion of the robots [17]. The presented results show that the proposed method can increase the swarm's coverage area for up to 10 robots. In the work presented by Beal, the development of a new process variant, reactive Levy Walks (LWs), and the application of this method to the problems of swarm dispersion and mixing is presented [18]. It is claimed that the Reactive LWs is an effective method for the dispersion and mixing of the swarms. Reactive LWs are asymptotically faster than prior approaches and provide both speed and continuous central coverage while requiring minimal sensing and no communication between swarm individuals. While Khaluf et al present Lévy properties disappearance in larger robot swarm sizes because of spatial interferences is presented [19]. Instead, they propose a novel algorithm to preserve Lévy properties at the collective level. Siebold and Hereford propose three algorithms for dispersing a swarm of robots that neither have a central coordinating agent nor have inter-bot communication throughout a search space [20]. Simulation results on five different search spaces with swarm sizes from three to fifty bots are presented in the paper including two other random-Walk-based dispersion algorithms. In the work presented by Vijay et al, an algorithm for dispersing a swarm of robots based on received signal strength using wireless communication between the robots is presented [21]. Webots™ based simulation results are presented for two different simulation scenarios, namely; concurrent and sequential scenarios. Results for both scenarios are similar. A comparison of two marsupial strategies for the initial deployment of swarm robots in unknown scenarios namely; Random and Extended Spiral of Theodorus is presented by Couceiro et al [22]. In the presented work, the first robots named scouts, are deployed with the cooperation of supporting agents, denoted as rangers. Results are presented using a performance metric based on dispersion. Pang et al present results for quantitative analysis of the searching efficiency of random walk (RW) Methods [23]. A RW method with step lengths are within a specified range to follow a given distribution and the correlations between the step length threshold, the area of the region, and the number of robots are provided based on the mean square displacement. The presented results imply that the area and the number of robots affect the optimal step length, that enables the robots to achieve the optimal search. Uğur and Turgut present a dispersion algorithm based on wireless signal strengths [24]. The algorithm is tested on a test-bed, called Kobot, for swarm-robotic studies which can generate signal strengths realistically, taking both the distance and relative orientations of the wireless sensors into account. Results for 5, 15, 25, and 50 robots placed in a 50m2 room are presented in the paper and dispersion becomes better with the increasing number of robots as expected [24].
In the literature, macroscopic-level modeling and control of swarm robots have emerged as popular research avenues, reflecting the growing interest in understanding and optimizing collective behaviors on a larger scale. Lerman et al reviewed methods for macroscopic modeling and analyzing swarm robotic systems. They focus on macroscopic modeling, collective behavior, and system optimization insights. Discusses distributed stochastic processes and simple probabilistic descriptions of swarm behavior. Compares the predictions to results of simulations and experiments [25]. Milutinović and Lima, focus on modeling and control of large robotic populations. Their paper models and controls large robotic populations using a stochastic approach. The study solved the optimal control problem using the Minimum Principle for Partial Differential Equations. In addition, they propose a centralized control strategy designed for large robotic populations [26]. Duncan et al concentrate on bioinspired strategies, such as Levy movements, showcasing their effectiveness in swarm robotics. Their study discusses mathematical models concerning collective behavior in biological systems and employs macroscopically partial differential equations to represent intricate robot movements. In particular, the paper emphasizes the importance of realistic metrics for optimizing swarm robotic systems. Quantitatively evaluates robot swarms using Lévy strategies for optimization [27]. Vigelius et al present a comprehensive approach to studying collective decision making in swarm robotics, linking individual-based descriptions to aggregate properties [28]. Lan and Li introduce a macroscopic state model to analyze swarm robot systems through time-delay differential equations. Their article focuses on studying the collective clustering task of swarm robot systems using the proposed model [29] .
1.1. The motivation of the study
Performing random exploring or searching activities such as scanning an area may lead to the repeated scanning of the same regions, increasing the computational load of the swarm. Distributing robots as evenly as possible across the working field will reduce the computational load while achieving maximum efficiency in a short timeframe. Moreover, this strategy is effective for searching in unknown environments. It offers a simple but effective and adaptable solution. This tactic can yield success across various swarm configurations, under any circumstances, and in any unknown environment. In this study, our goal is to analyze the dispersion of the swarm robots in an unknown environment by adjusting motion strategy parameters prior to the first movement of the robots. The simulations performed in this work are designed to understand what kind of scattering a robot swarm, which is left in an indoor environment to free fall from a certain height, will show ten seconds after being thrown into this environment. Since these swarm robots will not move until scattering occurs after a certain period of time from the start, they were designed as spherical objects. It is aimed to do the scanning of the unknown area with small rounded-shape robots.
The success of a swarm of autonomous robots is directly attributed to the effectiveness of their motion strategies. We also focus on whether the initial conditions of the motion strategies of the robots within the swarm can be optimized to achieve the best results. With this objective, rather than intervening during the processes, the results of the changes made at the initial stage are solely examined. The impact of the parameters used on the performance of the motion strategies is evaluated. In this context, the parameters under investigation exert an indirect influence by affecting the positions which are initial coordinates for motion strategies has started. In this study, the abbreviation 'PMP' is used to refer to these positions as previous motion positions (PMP).
Efforts are being made to understand how alterations in PMPs influence the preferred distribution of strategies within the swarm and how to rectify the disparities in outcomes among various strategies. If a more efficient action strategy can be selected by determining the PMP for a swarm and if this endeavor proves advantageous, the identification and application of such a strategy to our systems are aimed. As a preliminary step in these determinations and applications, validation and detection simulations are conducted through this study.
If a design can be made in a way that will affect the mission success of a robot swarm, this swarm will spread as homogeneously as possible in all directions at the beginning and complete the scanning/searching tasks quickly and efficiently. For this reason, the parameters were determined in this simulation study and the effect of these parameters on the scattering success was investigated.
Although all of these parameters can be interpreted individually, their combined effects create a complex structure. If the potential energy of a robot is high and the diameter of this robot is small, this robot will not collide with other robots while falling in volume and will be able to move in another direction quickly. However, if the coefficient of restitution (COR) of the robot is low, this will reduce the spread, as it will move by consuming more energy when it hits everywhere. However, this effect may cause the robot, which cannot move away from other robots, to collide with others and cause a robot to be thrown to a farther point with energy exchange. Apart from this, in another scenario, if the robot volume is large, the spreading may be positively affected due to excessive collisions, while if this robot falls from a lower height, the energy it will spend will be less, so it may fall to a closer point. For a more interesting result, besides all these, if this robot has high potential energy and if the COR value is high, we can see a scattering as the swarm falls to the ground. However, in this scenario, we can see that increasing the volume will bring us a lot of collisions in a short time, so the energy released by hitting the ground is more likely to be damped in a short time and the dispersion remains in a narrower area. The multiplicity of all these scenarios and the unknowns show us that we should make use of these simulations. If we look at these results, we can choose how the change of each parameter affects all the results. With the evaluations made accordingly, a swarm can be designed or the motions of the existing swarm can be tried to be predicted.
The study aims to improve the self-searching activities of swarm robots in challenging environments by evenly distributing them. The challenging and unknown environments make the problem difficult and complex to solve. The requirement for swarm robots to be simple, inexpensive, and small prevents robots from being reinforced in terms of hardware. However, it is important to note that a specific solution may not be applicable in all environments due to their unique challenges.
The objective of this study is to distribute the workload evenly in the environment while keeping the system simple and without disrupting the real-time activities of a swarm of robots. In the field of work, whether it involves search or any other task, the objective is to distribute the robots in a designated area. This ensures that they scan only the assigned area and move without disrupting the swarm structure. The simulation plan involves a two-stage intervention.
A more detailed explanation of the methodology is presented in the following sections. Then, in the results section, the outputs of simulations are examined under 2 headings: angular spreading and radial spreading. After the Results section, these outputs are discussed in the conclusion section.
2. Method
In this study, the Webots™ Simulator was preferred as the three-dimensional simulation environment to perform repetitive simulation experiments. In Webots™ , a complete mobile robotics set-up can be designed and adjusted, involving multiple robots sharing the same environment. Different properties like shape, color, texture, mass, and friction can be assigned to each object. Each robot can be equipped with various sensors and actuators. A sensor library in Webots™ lets you connect sensors to your robot model, adjusting properties like range and noise individually. Sensors include distance sensors, light sensors, cameras, and more. An actuator library offers various components such as motors, servos, LEDs, and grippers.
Using advanced OpenGL, Webots™ helps create complex simulated environments for mobile robots, including importing 3D models. Simulations run faster than in real time, with adjustable time steps. Accurate physics simulation, based on the Open Dynamics Engine, covers articulated parts.
Components' properties such as mass, friction, and collision objects can be specified. Servos are programmable for torque, position, and velocity. The Webots™ user interface supports interactive testing during simulations.
The main objective of this study is to investigate motion strategies. To ensure the precision of the results, its aimed at simplifying the experimental environment to avoid the potential influence of complex terrains. The rectangular arena proto has been selected as the testing ground, devoid of any significant obstacles or features. The rectangular arena proto, simulated in Webots™ , has the default features as follows. Gravity (g) of 9.81 m s−2, which mirrors the gravitational force on Earth, has been set. Coulomb friction and bounce velocity are set at 1 and 0.01 m s−1, respectively, influencing the material's behavior post-collision. Additionally, the drag force scale and the drag torque scale, set at 30 and 5 respectively, simulate air resistance or fluid drag, affecting the motion and behavior of objects within the simulated environment [30]. The absence of obstacles in the rectangular arena proto allows for an unobstructed observation of motion strategies, free from external interference. The specific parameters mentioned above are relevant because they closely mimic real-world physical conditions, thus ensuring the applicability of our findings.
In the literature, land robots have a larger usage and working area for a swarm workspace. There are many types of biomimetic robot mechanisms, but not all of them can be used effectively as members of a swarm.
The main selection factors require designing robots that are small, simple, and capable of interacting with the swarm as a member so that the swarm is least affected by environmental constraints. Within the scope of these restrictions, compact spherical robots could be a good choice. There were many different sizes and designs of spherical robots, but in this study, the basic ball-sized robot design was considered for the simulations [31].
In the simulations, as previously stated, rounded-shaped spherical robots were utilized. The selection of these robots, which move by rolling, was motivated by the main focus of the study: investigating motion strategies. After descending from a predetermined height via free fall, these robots pause until their bouncing behavior dissipates. Subsequently, they begin motion guided by motion strategies.
The robots designate calculated step points as targets and initially adjust their direction before rolling towards the destination. Each step in the study represents every calculated arrival target assisted by motion strategies. Importantly, these steps are not uniform, resulting in variations in the duration of movement of the robot.
The review article by Chase and Pandya emphasizes the fundamental driving mechanisms behind these robots. Spherical robots exhibit holonomic motion, enabling them to move freely in all directions without constraints. This property arises from their spherical shape and continuous rolling motion. Researchers have harnessed holonomy to design agile robots capable of navigating complex environments. Additionally, control moment gyroscopes (CMGs) play a pivotal role in propelling spherical robots, generating torque for precise control over orientation. Central to the study of spherical robots is understanding their dynamics and control [32]. In the article by Wang et al a decoupled dynamics approach is proposed for modeling and controlling spherical rolling robots. By breaking down the robot's dynamics into manageable subsystems, this method simplifies analysis and enhances control efficiency [33]. This modular approach enables smoother navigation and precise maneuvering, crucial for applications in complex environments. While not explicitly mentioning spherical robots, the study of Tomik et al provides practical insights into their creation. Spherobots typically consist of an outer spherical shell enclosing internal components, protecting sensitive electronics and mechanisms while allowing smooth rolling. Sensors, including accelerometers, gyroscopes, and proximity sensors, enable the robot to navigate its environment. Sophisticated control algorithms ensure stable and efficient movement, minimizing energy consumption and preventing collisions [34]. Another article written by Ren et al introduces a groundbreaking design. Their spherical robot features a heavy pendulum within its spherical shell, granting it amphibious capabilities. It can roll on land, float on water, and withstand extreme temperatures. The fully enclosed shell protects the robot's internal components from dust, water, and corrosive substances, ensuring longevity and reliability during extended missions [35].
Assuming flawless arrival at each designated point in every step, the robot reorients towards the newly calculated target upon reaching it and resumes rolling motion. The appeal of rolling spherical robots lies in their compact design, making them highly favored within the research community.
The behavior of robot swarms is influenced by a multitude of parameters, each of which plays a crucial role in shaping their collective dynamics and overall performance [36]. Key factors include swarm size, density, exploration-exploitation balance, connectivity between agents, noise levels, malfunctioning agents, memory capacity, iteration count, position visitation limits, neighboring information sharing, majority threshold, and minimum consensus achievement iterations. Furthermore, parameters such as the environment of the attraction of interest region, environmental conditions, the size of the swarm population, and external stimuli significantly impact the performance of the swarm in tasks such as resource collection [37].
Moreover, the steering of a robot swarm is heavily influenced by parameters related to repulsion, attraction, orientation, and influence, which directly affect tasks such as location determination, navigation, aggregation, and flocking [38]. These parameters collectively contribute to shaping emergent collective responses and overall swarm performance across various tasks and ambient contexts.
Understanding robot swarm behavior requires meticulous consideration of these diverse parameters, as they establish the foundational framework upon which swarm dynamics unfold. Recent research has focused on dissecting the influence of specific motion strategies, such as RW, LW, Markov Process (MP), and Brownian Motion (BM), on swarm behavior. This investigation aims to uncover the efficacy of these motion strategies in steering swarm dynamics towards desired outcomes while acknowledging their interplay with the aforementioned foundational parameters.
For instance, the choice and execution of motion strategies are intricately tied to factors like swarm release height, individual member radius, and mass, which directly influence initial conditions and post-collision mobility. Furthermore, parameters like COR and environmental conditions interact with motion strategies, affecting their effectiveness in facilitating navigation, aggregation, and flocking within the swarm.
Therefore, exploring motion strategies within the context of robot swarms acknowledges the significance of key parameters identified in prior research. By bridging these realms, this study aims to understand the complex interaction between motion strategies and swarm behavior.
As mentioned before, the main aim is to investigate the influence of various motion strategies on the behavior of a robot swarm consisting of 125 members. These strategies include RW, LW, MP, and BM. To conduct the analysis, the robots are initially treated as stationary spheres upon release into an empty area. This approach aids in simulation design and accounts for the robots' initial motionless state. The chosen parameters for configuration are the swarm's release height (H), radius (R) of individual swarm members, COR of the surface material, and mass (M). All these parameters affect the post-collision mobility of objects.
Simulations were conducted to comprehend the behavior of a swarm of robots in a challenging environment. The mentioned four parameters were selected to observe the impact of the release situation in the initial stage and the physical properties of the robots on the initial position before movement. The parameter choice was made because the potential energy of the robots in free fall will be converted into kinetic energy. According to the law of conservation of energy, this energy will be dissipated by effects such as friction and bouncing.
Equations (1) and (2) demonstrate the direct effect of height (h) and mass  ) on the energy generated. The parameters related to friction and damping are radius, which determines the surface area of the object, and COR, which affects the rebound potential
) on the energy generated. The parameters related to friction and damping are radius, which determines the surface area of the object, and COR, which affects the rebound potential
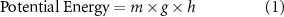
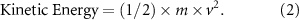
The selected values for the radius of objects, the height of the initial positions of objects, the COR of the covering material of the object and the mass of the parameters of the object are given in table 1.
Table 1. Parameters Used in The Webots™ Simulations.
| Parameters | Values of Parameters | ||
|---|---|---|---|
| Height of Swarm Before Free-Falling | 1 m | 2 m | 3 m |
| Radius of the Objects | 0.05 m | 0.075 m | 0.1 m |
| Coefficient of the Restitution | 0.4 | 0.65 | 0.96 |
| Mass of the Objects | 0.1 kg | 0.15 kg | 0.2 kg |
The values of all these parameters are chosen for the purpose. First, the coefficient of restitution value of the material from which the outer wall of the objects is made on the scattering was investigated. The objects were assumed to be designed with rubber, steel, and plastic walls, respectively, and the restitution coefficients of these materials were used. The coefficient of restitution values of the rubber, steel and plastic walls selected as materials are given as 0.4, 0.65, and 0.96, respectively [39, 40].
Second, as members of the swarm, these robots should have small size. So, the size is determined by using the rules of the world's oldest mini-robot contest Robocup. From this contest, we know that mini robot sizes are restricted to 18 cm diameters and a maximum 15 cm height. So, the radius parameter is determined as a max of 10 cm to get these restrictions.
Finally, the size of the world's most popular mini swarm robot E-puck was considered to determine the mass of the robots. The E-puck has 150 grams of weight [41]. And simulation mass values were selected around these values.
After getting the first position values of the objects, motion strategies were applied in MATLAB®. Each motion strategy was simulated 100 times and the results were stored in an Excel file as Cartesian coordination data and polar coordination data.
Totally with these simulation results, 324 different combinations were obtained in 2 different axis systems. With this data set, evaluations were started to monitor which parameters were affected more in each motion model and which motion models were sensitive to the initial environment.
2.1. Motion strategies
As mentioned previously, four motion strategies are emphasized. Using these strategies, the distribution of moving objects was observed in certain PMPs. In this study, robots initiate their movement with a free-fall motion within Webots™' three-dimensional (3D) simulation environment. However, upon landing on a flat and obstacle-free terrain, and given that the robots used are rolling spherical robots incapable of detaching from the ground, altitude data become unnecessary for step calculations. Subsequently, since robots remain connected to the ground throughout their active motion, step calculations are constrained to two dimensions (2D). Despite the initial adoption of a three-dimensional calculation methodology, a transition to a two-dimensional calculation strategy occurs during the second phase of the simulation due to the excessive computational burden associated with the former approach. The strategies were implemented in MATLAB® and run to see the effect of each one. The strategies used are as follows; RW Model, LW Model, BM Model, and MP Model. These strategies have been chosen from among the studies that take place frequently in the literature. General information about the models is mentioned below.
A RW is a mathematical model that describes a path that consists of a succession of random steps, each step taken in a random direction. The RW can be used to model a variety of processes, including the behavior of stock prices, the environment of diseases, and the diffusion of heat. The key feature of a RW is that the direction and magnitude of each step are determined randomly [42]. In this study, equations (3) and (4) are used to calculate the RW model. In a two-dimensional RW for robots, a direction is randomly selected from all possible directions in the plane at each step. The magnitude of each step is determined randomly, allowing for variations in step size. This process can be visualized as the robot navigating through space, taking steps in different directions
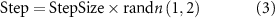
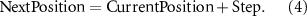
The LW Model is a variant of the RW distinguished by its long-tailed steps, indicating that the distribution of step sizes extends further than the Gaussian distribution. The step calculation equation for the LW Model is given by:
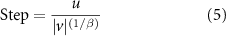
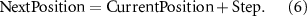
In a LW, the step sizes in the RW follow a Levy distribution, which has a longer tail than the Gaussian distribution. This means that the walk is characterized by occasional large steps and many small steps. The LW has been used to model a variety of natural phenomena, including the foraging patterns of animals and the diffusion of particles in complex systems [43, 44].
Equations (5) and (6) are employed for the 2D calculation of the LW Model. In this study, a MATLAB® function developed by Yang and Deb is utilized for implementing equation (5), as [45, 46]. This function generates random numbers u and v from normal distributions to produce Levy steps in the specified dimensions. u and v are variables drawn from normal distributions and are used in the calculation of random step sizes. Beta, on the other hand, is an index of the Levy distribution that influences the distribution of calculated step sizes. It has both a random and a scale effect. The beta value affects the tail of the Levy distribution, which determines the probability of selecting long steps.
A MP is a mathematical model for a sequence of events in which the probability of each event depends only on the state attained in the previous event. In other words, the future state of the system depends only on its current state and not on its history. MPs can include RWs as a special case, but they can also describe more complicated systems where the dependence between events is more complex [47]. Equation (7) provides a straightforward representation of this algorithm. It provides a clear outline of the algorithm to calculate the next step in the two-dimensional movement of the robot. In this equation, 'NextPos' denotes the next position calculated for the subsequent step, while 'CurrentPos' refers to the current position of the robot.
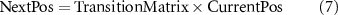
BM can be mathematically modeled in various ways. The most fundamental model is known as BM (Wiener process), where particles move randomly in a stochastic process. Mathematically, the expression for BM represents the change in position of a particle over a specific period of time. In one-dimensional BM, it can be expressed as a stochastic differential equation:
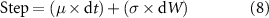
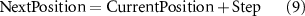
Here, Step represents the change in the particle's position, µ represents the drift (trend) term, and ( ) represents the random term. dW is a stochastic process known as the Wiener process and consists of independent, time-varying random variables with a Gaussian distribution. This mathematical expression shows that the particle moves randomly over a given period of time and may exhibit a trend term µ for changes. σ is a parameter that controls the randomness of the motion. In this investigation, the BM model was specifically applied to simulate 2D robot behavior using these equations.
) represents the random term. dW is a stochastic process known as the Wiener process and consists of independent, time-varying random variables with a Gaussian distribution. This mathematical expression shows that the particle moves randomly over a given period of time and may exhibit a trend term µ for changes. σ is a parameter that controls the randomness of the motion. In this investigation, the BM model was specifically applied to simulate 2D robot behavior using these equations.
In robotics, BM can be used to model or simulate robot motion or behavior. For example, when an autonomous robot requires random behavior during navigation, BM can be employed. By introducing stochastic variations to the robot's position or orientation using the BM model, randomness and chaos can be added to the robot's motion. In this way, the BM model allows robots to exhibit more realistic and dynamic behavior. Particularly in scenarios such as navigation, obstacle avoidance, or exploration, where the robot needs to move randomly or turn in a chaotic manner, the BM model can be utilized.
These four models provide different ways to model the position and motion of robots. The RW offers completely random motion, the LW allows for longer distances with larger steps, the BM adds randomness and chaos, and the MP models state-dependent motions. The choice of which model to use depends on the specific requirements and nature of the robot's behavior for a given task or application.
2.2. Simulation procedure
For each combination of parameters and strategies, 100 trials are performed, each trial consisting of 100 steps. Position data is recorded every 10 steps, leading to a total of 10 position data points for each trial. The final results are obtained by calculating the average of the results of the 100 trials for each combination of parameters and strategies.
Two factors were considered to evaluate the results: the absence of aggregation and the achievement of scattering. In line with the purpose of the study, the swarm should scatter without clustering and without moving too far apart. When analyzing the experimental results for these two criteria, two categories were defined: spreading in polar coordinates and spreading in Cartesian Coordinates. Consequently, data related to radial spreading were collected for scattering, and data related to angular spreading were collected for aggregation. For angular spread, the polar axis was virtually divided into 8 equal segments, and the number of robots in each segment and their standard deviations were examined. In radial spreading, the distance of each robot from its starting point in Cartesian Coordinates was determined. To obtain more reliable data for radial spreading, data for marginal movements in the swarm were excluded. Therefore, the inter quartile range (IQR) was used. The IQR values helped us assess the movements of the swarm population, excluding the least distant 25% and the most distant 25%.
3. Result
When it comes to a swarm's search and observation process, we claim that the optimal approach is to distribute the swarm as uniformly as possible. As a consequence, each robot will scan its own divided area, leading to comprehensive coverage due to the nearly uniform distribution.
As mentioned before, to examine whether a swarm is distributed as uniformly as possible over an area, we studied two criteria. One of them was scattering and the other was aggregation. Scattering provides us with information about whether the swarm spreads out from all directions within that area, while aggregation data indicates how much tends to cluster these robots in the field. In scattering, we aim to position robots in the area from all directions. Additionally, in aggregation, we expect each robot to be optimally far from each other, but not so far from each other as to go far away from the swarm. When these expectations are met, we can admit that the swarm is distributed as effectively as possible within an area.
In this section, the results of the simulations will be evaluated. The results of the study were analyzed in two categories: scattering and aggregation. For these two categories, this section contains two sections: Angular spreading and radial spreading results.
3.1. Angular spreading
While evaluating the obtained results, the initial focus was on detecting and scaling the scattering. At this point, a systematic method was developed to comparatively assess the scattering states of these robots. The aim was to measure the angular spreading of these robots in a 2-dimensional plane. For this purpose, the two-dimensional plane was divided into a total of 8 equal parts that span 45 degrees, and an evaluation was performed by examining how many robots fit into each part and considering the standard deviation between these robot distributions.
In these results, the outcomes for each model were categorized based on variables and applied motion strategies. Through these categorizations, the impact of changes in each parameter was observed on the results of motion strategies. Furthermore, it was observed how the strategies yielded different outputs according to the standard deviation. In summary, this process yielded a comprehensive understanding of the effects of changing variables and motion strategies on the outcomes, as well as how strategies make varied results based on the standard deviation.
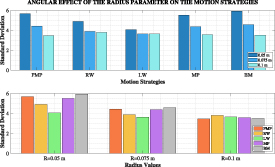
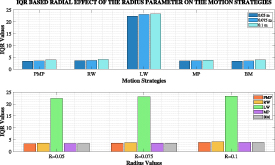
It can be observed how the radius of a robot affects the PMP and motion strategies' outputs in figure 1. According to these results, the scattering in free-falling swarm robots achieves a better distribution as the radius increases in the initial stage. Consequently, it is seen that the motion strategies follow this changing trend. Although the results of all motion patterns were correlated with the baseline values, some differences can be observed. Accordingly, the effects of parameter changes for the MP Model and the BM Model are observed proportionally close to each other. On the other hand, although correlations are observed in RW and LW models, the responses to parameter changes remain proportionally smaller. In particular, it can be said that the parameter change affects the LW Model less than the others. However, it is also seen that RW and LW Models can achieve better angular spreading.
Figure 1. Angular effect of the radius parameter on the motion strategies.
Download figure:
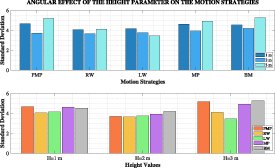
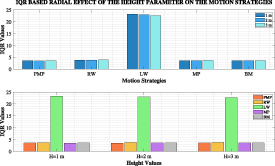
Standard image High-resolution imageThe effect of the height at which the swarm is initially left for free-falling is presented in figure 2. It is clear that the initial height affects the PMP, which in turn affects the final results of the motion strategies. In this graph, the increase in height first improves the standard deviation and then causes an increase. It should be noted that motion models have a correlation with the PMP, but the LW model differs from the other strategies. The model seems to tend to perform better dispersion despite the initial conditions.
Figure 2. Angular effect of the height parameter on the motion strategies.
Download figure:
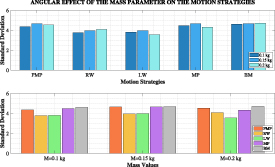
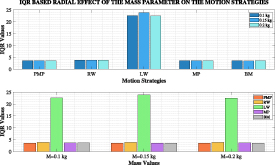
Standard image High-resolution imageAs presented in figure 3, among all parameters that has the least effect on scattering is observed as the change in the mass parameter. The small effect on the PMP seems to have caused the results of the motion patterns to be not very different from each other. It seems that the LW Model caught the best distribution, and the BM Model gave worse results than the PMP. One of the obvious results is that the RW Model and the LW Model tend to show better scattering on the basis of this variable as well.
Figure 3. Angular effect of the height parameter on the motion strategies.
Download figure:
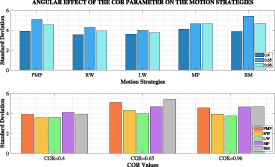
Standard image High-resolution imageThe effect of the COR parameter change on the results is presented in figure 4. In this graph, unlike the others, it is observed that the only parameter that affects all motion patterns in the same trend is COR. However, while the increase in the COR parameter gives bad results in the standard deviation, it is seen that this result starts to improve later on. According to the initial conditions, it is seen that the BM Model has the least performance, and the LW Model has the best scattering.
Figure 4. Angular effect of the COR parameter on the motion strategies.
Download figure:
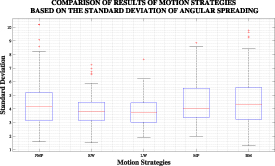
Standard image High-resolution imageFigure 5 constructed based on standard deviation values displays the results of all combinations of parameters according to their standard deviation. When considering the distribution of standard deviation values, the BM Model is closest to the PMP, followed by the MP Model. However, RW and LW models show differentiation. It can be observed that these two models have narrowed the range of standard deviations in PMP. Furthermore, a noticeable concentration around the mean values is observed.
Figure 5. Comparison of results of motion strategies based on the standard deviation of angular spreading.
Download figure:
Standard image High-resolution image3.2. Radial distribution
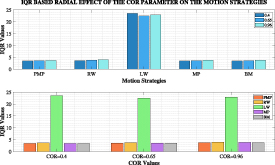
In this section, the radial distribution of the robots is analyzed. Figures 6–9 present the IQR-based radial effects of each parameter—radius, height, coefficient of restitution (COR), and mass, respectively—on the motion strategies. The radial distribution means how far robots have spread around the searching field from the initial position of the swarm. It was examined how the swarm structure was distributed as a result of different values of the parameters and PMP and movement strategies. In order to make an evaluation, the IQR values of the distributions of the robots left in the environment in their final form were examined. This gives information about how the swarm is dispersed. Instead, the variance could also be examined and it could be said that for increasing distribution, it spreads over a much wider area and the probability of gathering in this distribution decreases. However, this comment would be an understatement. Because marginal results affecting the variance may lead to wrong conclusions. Instead, it is necessary to take advantage of another determining feature that eliminates marginal results. For this reason, IQR was preferred. According to this measurement, median values of 50% were evaluated, excluding the 25% closest to the starting point and the 25% furthest from the distribution. The distance of the average of these values to the origin was calculated. Based on this value, it was checked how widespread the distribution was. This value allowed for a better inference away from marginal robots that could affect the variance.
Figure 6. Radial effect of the radius parameter on the motion strategies.
Download figure:
Standard image High-resolution imageFigure 7. Radial effect of the height parameter on the motion strategies.
Download figure:
Standard image High-resolution imageFigure 8. Radial effect of the mass parameter on the motion strategies.
Download figure:
Standard image High-resolution imageFigure 9. Radial effect of the COR parameter on the motion strategies.
Download figure:
Standard image High-resolution imageWhen examining these IQR plots, the first noticeable aspect is the differentiation of LW model outputs from the outputs of the other models. RW, MP, and BM models show similarity with each other and with PMP outputs. Increases in the Radius, Height, Mass, and COR parameter values have led to similar increases in PMP results. However, except for the LW Model, other models exhibit similar patterns in all parameters except Radius, where they show different variations. Another noteworthy observation in the graphs is that the models that do not cover extreme distances are in harmony with PMP. The large IQR value of the LW Model indicates that it is significantly distant from the starting points of the 75% population. However, this also suggests that the 75% population of the other models has navigated around the starting positions.
4. Discussion
In this study, during the initial phase until the getting PMP, robots experienced free fall and started their motion from the PMP location 10 s later. The effects of the first stage of this study can be observed by examining how the initial parameters lead to changes in PMP. In this regard, it has been observed that an increase in the radius parameter causes a linear increase in PMP. Increasing the radius increases the calculated surface area, thereby expanding the potential collision area [48]. This situation may lead to a faster damping of kinetic energy in the system. The increased radius can result in the spreading of collision interactions and the distribution of energy over a wider area.
However, the Mass parameter, yielded similar results at the four levels for standard deviation in PMP in the case of angular spreading, while it resulted in a linear trend in PMP for radial distribution. Increasing mass elevates potential energy, which, in turn, raises the levels of kinetic energy converted from potential energy [49]. This can lead to more collisions occurring and energy being damped in a shorter time. The impact of increased mass can enhance the density of environmental interactions, potentially enabling the system to reach equilibrium more rapidly.
The falling height of the robots is observed to be correlated in radial distribution for both the initial and PMP results, while the situation differs for angular spreading. Increasing height raises the potential energy amount and augments kinetic energy, potentially amplifying collision interactions and leading the system to undergo a faster energy exchange process.
Examining the effects of material values of swarm robots on the COR, it is observed that an increase in this value linearly affects the radial distribution. Although the angular deviation values may not exhibit linearity, they show a tendency to increase. Variation in the COR value could significantly enhance the bounce effect [50], potentially leading to increased entropy and reduced predictability of the results.
Considering all these results, it can be concluded that the radial effects of the parameters utilized in the study have a linear structure on PMP. According to the simulation results, the spreading effect can be scaled according to these parameters. Based on the angular spreading data used in the study, it is concluded that an increase in all parameters affects PMP in an increasing direction, but this effect cannot be scaled due to the observed variations.
When the results are examined, it is evident that PMP influences the outcomes, especially in the context of angular spreading. Moreover, the larger the standard deviation value of PMP, the more pronounced the impact of strategies on PMP becomes. When the standard deviation value in PMP is 4 or less, not only is there no overlap with the outputs of one-to-one strategies, but also no significant differences are identified in these cases. Taking into account all these findings, it is possible to assert that changes in PMP values affect the outcomes of motion strategies, particularly in the context of angular spreading.
For the LW Model, it is observed that it strongly suppresses values with standard deviations of 4 and above, bringing them down to average levels. However, at lower standard deviation levels, it exhibits effects similar to those of other models. For the RW Model, can be said that it has the second-largest impact on angular spreading after the LW Model. The results of the RW model are clearly influenced by PMP. When examining the results of the BM Model, it is evident that it is strongly linked to PMP but does not have a significant effect on changing it.
In addition, looking at the standard deviation comparison graph under angular spreading results, the fact that the average values of all strategies are close to each other indicates that these strategies are mostly similar to each other. Observing figure 5, it is possible to say that the BM Model and MP Model are the strategies most dependent on PMP. However, the RW and LW models, while being influenced by PMP, are also seen as the two strategies that most significantly alter it.
In conclusion, it can be stated that the LW model provides the best performance for angular spreading across all values.
When looking at the radial distribution results, the IQR data, it is observed that LW makes a significant difference. At this point, all strategies except LW have followed the trend of variation of PMP. Apparently, these strategies have not ventured far from their starting points and have conducted searches in close proximity. However, in LW, there is an aggressive expansion, and robots are dispersed over a wide area. This is because the algorithm formulated for LW makes larger choices for step intervals compared to other strategies. It can be interpreted that this version of LW is suitable for scanning large areas but is also aggressive enough to disrupt communication between robots.
By adjusting the beta and alpha terms affecting the Gauss Distribution tail for LW, this distribution can be spread over a smaller area. Notably, in IQR graphs, models that do not cover extreme distances tend to be compatible with PMP. Aggressive movements reduce predictability and render models less scalable.
It can be stated that there is an expansion for LW, but simultaneously, the aggregation rate is reduced. In LW, random steps and sizes are observed to be random as well.
5. Conclusion
This study examines the effects of initial conditions on the distributions of a swarm. The aim is to establish a general framework for swarms. In this context, a simulation experiment is designed using physical parameters such as radius, height of swarm, mass, and COR, along with robot motion strategies such as RW, LW, BM, and MP. Initially, in the passive mode, the effects of physical parameters on the distribution of free-falling robots are observed, followed by an investigation into how initial positions affect motion strategies after transitioning to the active mode. Finally, the angular and radial distributions are evaluated to analyze the overall dispersion. To make a meaningful comparison, it is necessary to simulate strategies with different calculation steps and theories under the same method and conditions. Only then can a true comparison be made. The results of these methods have been compared and analyzed. In addition, IQR data have been used to eliminate extreme values resulting from differences in methods, allowing for more accurate interpretations. This comparison is essential to maintain the consistency of the sample.
The main concern is the interaction between parameters and strategies, in order to find solutions to these challenges. In the designed simulation study, the isolated effects of parameters are examined first, followed by an exploration of how motion strategies affect distributions. The simulation, developed in two stages, enables one to obtain isolated results. Thus, the effects of parameters on distributions are traceable, and how initial conditions influence motion strategies is observed.
Studies in this field generally focus on the effect of changes in the swarm population on results [17, 51]. In addition, studies that include the movement strategies used are generally studies in comparison to each other and parameters such as the velocity of swarm robots or the pathways determined during the process [52, 53]. The innovative aspect of this study is that the effect of changes in initial conditions is examined both in terms of swarm distribution and motion strategies.
This study provides valuable information on the impact of motion strategies on robot swarm behavior. The results highlight the potential of different strategies to shape collective motion patterns. The results found are data that can be used when designing many robot structures. New studies can extend this analysis by considering more complex environments, diverse types of robots, and real-world applications. Furthermore, the results of this study, including a homogeneous swarm structure, can be used to design a robot swarm with a heterogeneous structure for a better radial and angular distribution.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Author contributions
The authors contributed equally to the preparation of the paper.
Conflict of interest
The authors declare that there are no conflicts of interest.
Supplementary data (<0.1 MB XLSX)
Supplementary data (0.4 MB XLSX)
Supplementary data (0.4 MB XLSX)
Supplementary data (0.4 MB XLSX)
Supplementary data (0.4 MB XLSX)
Supplementary data (<0.1 MB XLSX)