Abstract
Solar reflective 'cool roofs' absorb less sunlight than traditional dark roofs, reducing solar heat gain, and decreasing the amount of heat transferred to the atmosphere. Widespread adoption of cool roofs could therefore reduce temperatures in urban areas, partially mitigating the urban heat island effect, and contributing to reversing the local impacts of global climate change. The impacts of cool roofs on global climate remain debated by past research and are uncertain. Using a sophisticated Earth system model, the impacts of cool roofs on climate are investigated at urban, continental, and global scales. We find that global adoption of cool roofs in urban areas reduces urban heat islands everywhere, with an annual- and global-mean decrease from 1.6 to 1.2 K. Decreases are statistically significant, except for some areas in Africa and Mexico where urban fraction is low, and some high-latitude areas during wintertime. Analysis of the surface and TOA energy budget in urban regions at continental-scale shows cool roofs causing increases in solar radiation leaving the Earth–atmosphere system in most regions around the globe, though the presence of aerosols and clouds are found to partially offset increases in upward radiation. Aerosols dampen cool roof-induced increases in upward solar radiation, ranging from 4% in the United States to 18% in more polluted China. Adoption of cool roofs also causes statistically significant reductions in surface air temperatures in urbanized regions of China (−0.11 ± 0.10 K) and the United States (−0.14 ± 0.12 K); India and Europe show statistically insignificant changes. Though past research has disagreed on whether widespread adoption of cool roofs would cool or warm global climate, these studies have lacked analysis on the statistical significance of global temperature changes. The research presented here indicates that adoption of cool roofs around the globe would lead to statistically insignificant reductions in global mean air temperature (−0.0021 ± 0.026 K). Thus, we suggest that while cool roofs are an effective tool for reducing building energy use in hot climates, urban heat islands, and regional air temperatures, their influence on global climate is likely negligible.
1. Introduction
Solar reflective 'cool' roofs (e.g. white roofs) absorb less sunlight than traditional dark roofs, and consequently stay cooler in the Sun. Cool roofs therefore transmit less heat to the building below and the atmosphere above, and can thus cool the atmosphere. Widespread adoption of cool roofs is thought to be an effective strategy for mitigating 'urban heat islands' (Synnefa et al 2008, Taha 2008a, Lynn et al 2009, Oleson et al 2010, Li et al 2014), a phenomenon in which urban areas are warmer than their surroundings due to the ubiquitous use of absorptive surfaces, less vegetation cover, and abundant anthropogenic heating in cities (Oke 1973, Li and Bou-Zeid 2014, Tao et al 2015). Cool roofs have also been proposed as a geoengineering strategy to partially and temporarily counter warming associated with anthropogenic climate change (Akbari and Matthews 2012) by increasing solar radiation reflected by Earth. The albedo of other surfaces on Earth could analogously be intentionally increased including that of agricultural land (Campra et al 2008, Wilhelm et al 2015), forest (Luyssaert et al 2014) and urban pavements (Santamouris 2014).
Past research has suggested that cool roofs could effectively mitigate urban heat islands. For example, Oleson et al (2010) estimate that adopting cool roofs in cities around the globe could decrease the difference between urban and rural air temperature by 0.4 K on average. Synnefa et al (2008) show that in Athens, increasing roof albedo by 0.45 and 0.67 could lead to a decrease in urban air temperature at noon as high as 1.5 K and 2.2 K, respectively. Georgescu et al (2014) estimate that under a scenario assuming maximum urban expansion by 2100, the adoption of cool roofs could reduce summertime urban surface air temperatures by 1.2 K in Florida to 3.2 K in the Mid-Atlantic United States of America. Taha et al (1998) and Taha (2008a, 2008b) show that large-scale increase in urban albedo can reduce summertime 2 pm air temperatures in various cities in the United States, and moreover decrease building energy use and mitigate photochemical air pollution.
The influence of cool roofs on regions larger than urban scale is more complex due to possible atmospheric feedbacks that may behave differently on mesoscale versus larger scale meteorology. In addition, as the spatial extent of the region of analysis increases beyond the urban scale, the magnitude of climate response from the urban albedo modification decreases and can approach the magnitude of natural climate variability, making it difficult to tease out the influence of the initial forcing. Millstein and Menon (2011) perform simulations suggesting that employing cool roofs in cities can lead to statistically significant decreases in summertime surface air temperature over Northern California of 0.011 K, and statistically insignificant decreases over the United States of 0.004 K. They also find insignificant increases in summertime surface air temperatures in Texas and Florida, which they attribute to an atmospheric feedback causing fewer clouds, less precipitation, and lower soil moisture.
Investigating the climate impacts of cool roofs at the global scale is challenging due to difficulties in characterizing urban physical properties and physics processes in global models with coarse spatial resolution. Instead, some research has simplified the study of the global impacts of cool roofs by estimating its associated radiative forcing and then inferring climate impacts by computing the CO2 reduction that would cause equivalent forcing. Akbari et al (2009) estimate the global radiative forcing of installing high-albedo roofs worldwide (i.e. increasing urban albedo by 0.06) to be −2.6 × 10−2 W m−2, which is equivalent to a one-time CO2 emission reduction of 25 billion tonnes (Gt). Menon et al (2010) employ a detailed land surface model to estimate radiative forcing from cool roofs, and estimate the equivalent CO2 emission reduction as 31 Gt.
A few past studies use climate models to directly estimate the influence of cool roofs on global scale temperature. Using an Earth system model without treatment for urban physics, Akbari et al (2012) simulate global average surface air temperature changes after increasing the albedo of land in 20 °S–20 °N and 45 °S–45 °N, respectively, and scale the results by the fraction of urban area to land area. They report a global temperature decrease of 0.01–0.07 K from increasing urban albedo by 0.1, offsetting 25–150 Gt CO2 emissions. Using the same model and similar methodology, Akbari and Matthews (2012) estimate that increasing urban albedo by 0.1 can offset CO2 emissions by 160 Gt. However, the atmospheric component in the Earth system model used in these studies is a simplified two-dimensional energy and moisture balance model, lacking cloud and aerosol schemes, as well as feedback processes in the atmosphere. In contrast, Jacobson and Ten Hoeve (2012) adopt a sophisticated Earth system model that includes cloud feedback processes and subgrid urban parameterizations. They estimate that installing white roofs would actually increase global average air temperature by 0.07 K. They attribute this increase in air temperature to (1) decreased surface air temperature causing lower sensible and latent heat fluxes, contributing to a decrease in cloudiness, (2) increased sunlight reflected by newly adopted cool roofs being absorbed by aerosols in the atmosphere, and (3) feedbacks of local changes to global scale causing cloud reductions and snow and sea ice melting in Antarctica. Given that they counter-intuitively conclude that cool roofs can increase global temperatures, these results should be verified by additional research. While Oleson et al (2010) implement urban parameterizations in a global land model, and couple it with an advanced global atmospheric model to investigate the influence of cool roofs on urban climate, they do not report global average temperature change caused by cool roofs. Note that one additional distinction between the two studies is that the global model used in Jacobson and Ten Hoeve includes a fully dynamic ocean model, while that of Oleson et al uses fixed sea surface temperatures, which would tend to inhibit climate feedbacks.
The radiative benefits and climate impacts of cool roofs can be influenced by aerosol loadings and clouds. Millstein and Fischer (2014) show that in five Indian cities, where aerosol optical depth (AOD) is high, aerosols reduce the radiative benefits of cool roofs (i.e. the additional outgoing solar radiation at the top of the atmosphere due to installation of cool roofs) by 70%. Past studies also highlight cloud feedback as an important factor when evaluating the influences of cool roofs on climate (Millstein and Menon 2011, Jacobson and Ten Hoeve 2012). Nevertheless, Jacobson and Ten Hoeve is the only past study that investigates the global impacts of cool roofs using a model that accounts for atmospheric feedbacks including cloud changes. There is also a lack of research that quantifies and compares these influences in different regions.
To help overcome the aforementioned gaps in research on the influence of cool roofs on climate, we investigate in this research the potential climate impacts of cool roofs on different spatial scales—urban-scale (i.e. urban heat islands), continental-scale, and global-scale. We use an Earth System Model that includes a latest generation three-dimensional atmosphere model, a land model that resolves urban physics, and a slab ocean model. Changes in energy fluxes, temperature, cloud fraction, snow, and precipitation, after increasing roof albedo in cities around the globe, are predicted. We also investigate to what extent the radiative benefits of cool roofs are influenced by aerosols and clouds in several countries (i.e. United States, China, India, and Europe).
2. Method
2.1. Model description
We use the Community Earth System Model (CESM) version 1.2.0 developed by National Center for Atmospheric Research, which couples the Community Atmosphere Model version 5.0 (CAM5), the Community Land Model version 4.0 (CLM4) (Lawrence et al 2011), and the slab ocean model. CAM5 uses a two-moment stratiform cloud microphysics parameterization (Morrison and Gettelman 2008). Deep convection is parameterized by Zhang and McFarlane (1995). Moist turbulence and shallow convection are parameterized by Park and Bretherton (2009). The radiative transfer calculations are performed by RRTMG (Rapid Radiative Transfer Model for General circulation model applications). The aerosol life cycle in the model is represented by the modal aerosol module MAM3 (Liu et al 2012). Aerosols can affect cloud formation by acting as cloud condensation nuclei and ice nucleating species (solution droplets or ice nuclei). CAM5 physics with MAM3 chemistry, coupled with CLM, has been scientifically validated against observations (Tilmes et al 2015). Compared to other versions of CAM (e.g. CAM3 and CAM4), CAM5 has updated cloud parameterizations that are increasingly physics based and show better agreement with observations of cloud radiative forcing, cloud fractions, precipitation rate, frequency of deep and shallow cumulus, as well as other cloud-related variables (Park et al 2014). More detailed information about CAM5 can be found in Neale et al (2010). Emissions of anthropogenic aerosols and their precursors are from CMIP5 and representative of the year 2000 (Lamarque et al 2010). Dust and sea salt emissions are calculated online as a function of wind speed, vegetative cover, soil properties, and sea surface temperatures. Though noticeable biases exist, CAM5 with MAM3 can reproduce the temporal and spatial patterns of observed aerosol concentrations and optical properties (Liu et al 2012), and AOD in many regions around the world (Ban-Weiss et al 2014). The model is run at a horizontal resolution of 1.9° × 2.5° (latitude × longitude), with 30 layers in the vertical from the surface to 2 hPa.
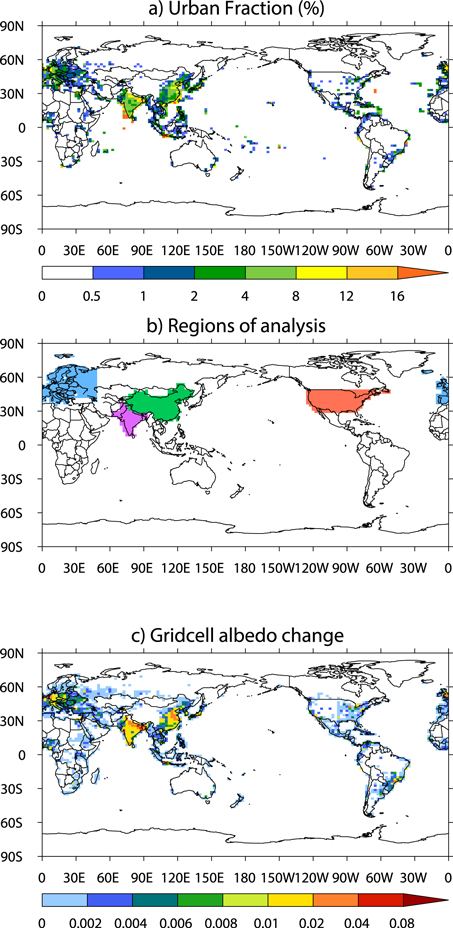
Figure 1(a) shows the global distribution of 'urban fraction' (i.e. the fraction of land area within each model grid cell that is urban) in CLM4. The urban portion of a grid cell is treated as a canyon system consisting of five facets: roof, sunlit wall, shaded wall, pervious floor, and impervious floor. Temperatures, sensible and latent heat fluxes, incident and reflected radiation, and heat storage are calculated for each individual surface in the urban parameterization. The geometry of an urban canyon is characterized by building height, and the ratio of building height to canyon floor, which allows for computing multiple reflections and trapping of radiation by canyon surfaces. Waste heat fluxes due to space heating and air conditioning are also considered by comparing the interior building temperature to prescribed maximum and minimum comfort temperatures. Model evaluation in Mexico City and Vancouver shows that the urban parameterization in the land model in general captures the diurnal cycles of surface temperatures and energy fluxes (Oleson et al 2008a, 2008b, 2008c, 2010).
Figure 1. Global maps showing (a) distributions of urban fraction (i.e. the fraction of land area within each grid cell that is urban), (b) the four continental-scale regions of analysis: the United States (US), Europe (EU), China (CN), India (IN), and (c) albedo change 
in each grid cell due to increasing roof albedo from 0.15 to 0.9, calculated using equation (1). Note that 
represents only albedo change from cool roofs, and not from feedbacks that lead to changes in snow and ice.
Download figure:
Standard image High-resolution image2.2. Summary of simulations
We investigate the differences in equilibrium climate states of two cases. In the DARK case, roof albedo is set to 0.15 (traditional dark roof albedo), and in the COOL case, roof albedo is set to 0.9 (cool roof albedo). Currently available cool roof products attain albedos of near 0.9 even after considering albedo decreases associated with aging and soiling (see the Rated Products Directory at Cool Roofs Rating Council http://coolroofs.org/). Oleson et al (2010) choose a similar roof albedo of 0.91 in their cool roof simulation. The difference in dark and cool roof albedo of 0.75 in our study is chosen as an upper bound in order to maximize the climate forcing and subsequent response in the climate model. Note that we intentionally choose an idealized spatially uniform roof albedo for DARK since we aim to investigate how atmospheric responses vary spatially, and having spatially varying albedo differences would complicate this analysis.
The model is run assuming dark roof albedo from 1985 to 1999 as a spin-up, and then branches into six ensemble simulations: three for the COOL case with high roof albedo (0.9) and three for the DARK case with low roof albedo (0.15). Each ensemble simulation is run for 40 years, and the first 10 years are discarded as spin-up; only the results from 2010 to 2039 after the model has attained near steady state are used for analysis. For each case, the first ensemble member is a continuation of the initial spin-up simulation (i.e. from 1985 to 1999). The second and third ensemble members are started from 1 November 1999, and 1 December 1999 respectively and are initialized using model output from the initial spin-up run. Averaging among the three ensemble members reduces the influence of natural climate variability (i.e. climate variability due to natural processes in atmosphere, ocean, and land) (Kay et al 2015), helping single out the climate response due to the introduced forcing (i.e. albedo increase from cool roofs). The Student T-test with 3 × 30 = 90 annual values for each case is used to assess whether the climate response from implementing cool roofs is statistically distinguishable from the natural climate variability.
2.3. Regions of analysis
Besides investigating changes in climate in cities around the globe, we also focus on four continental-scale regions: United States, China, India, and Europe (see figure 1(b)). We increase roof albedo in all grid cells with nonzero urban fraction. Figure 1(c) shows the grid cell-averaged albedo change induced by cool roofs 
estimated using equation (1)
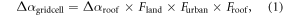
where 
is the change in roof albedo (0.9 − 0.15 = 0.75), 
is the fraction of a grid cell that is land, 
is the fraction of land area that is urban, and 
is the fraction of urban area that is roof. Note that while variations in snow and ice can influence simulated surface albedo, we intentionally compute 
using model input data so that it includes only contributions from roof albedo, and thus represents the forcing without the climate response.
In this study, all analyses in the four regions defined above use only grid cells that are conditionally sampled for 
This value is chosen to maximize the contribution of the forcing (i.e. roof albedo increase) to the computed total climate response while decreasing the influence of natural variability (i.e. in areas without roof albedo increases). Thus, continental-scale results are representative of regions with urban areas, and are not averages over the entire country.
3. Results and discussion
3.1. The effects of cool roofs on urban heat islands
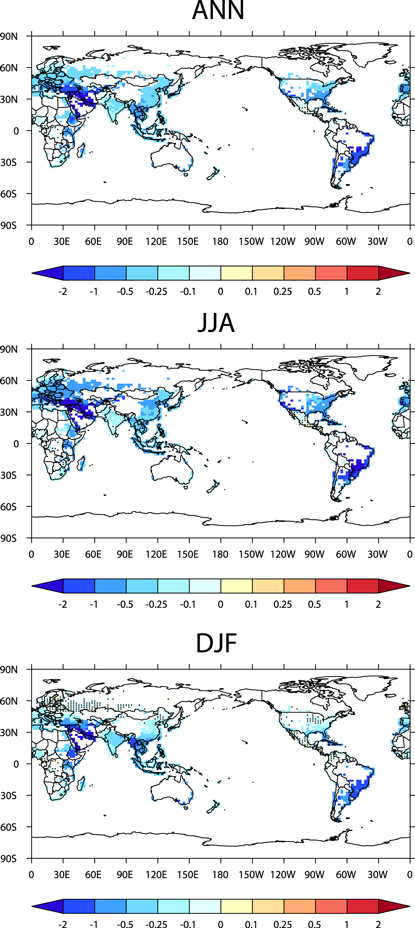
Figure 2 shows the impacts of adopting cool roofs on urban heat islands around the globe. It is important to note that our model is run at a coarse resolution, and each grid cell is comprised of both urban and rural portions. Following Oleson et al (2010), the urban heat island is defined as the surface air temperature (i.e. air temperature at 2 m) difference between urban and rural areas in each grid cell. The rural temperatures represent the air temperatures over vegetated and bare soil surfaces. Urban heat islands are shown to decrease around the globe in summer, winter, and annually. Decreases are statistically significant in most regions, except in some high-latitude areas in winter, and in some parts of Africa and Mexico that have low urban fraction. The annual- and global-mean urban heat island is reduced from 1.6 to 1.2 K. Our results slightly differ from Oleson et al (2010), which suggests that wintertime urban heat islands can increase in high latitudes due to an increase in anthropogenic heating, and estimates that the annual- and global-mean urban heat island is reduced from 1.2 to 0.8 K. Differences between our study and Oleson et al (2010) could be partially attributed to different assumed dark roof albedo; they assume a spatially varying albedo distribution with an average of 0.4. In addition, although we run Earth system models with similar atmosphere and land components, our model is also coupled to ocean and ice modules whereas Oleson et al (2010) use only prescribed sea surface temperatures. Moreover, we use the updated version of the community atmospheric model (version 5), while Oleson et al use the previous version (CAM4). Nonetheless, both Oleson et al (2010) and our study suggest a global mean reduction in the urban heat island of 0.4 K and show a very similar spatial pattern of the reduction. Comparing figure 3 to figure S1, the magnitude of urban heat island reduction follows the spatial pattern of urban absorbed solar radiation, consistent with the findings of Oleson et al (2010). In the United States, China, India, and Europe, averaged reductions in urban heat islands (for grid cells with 
are 0.55 K, 0.43 K, 0.24 K, and 0.36 K, respectively.
Figure 2. Changes in urban heat islands (urban minus rural surface air temperature) from increasing roof albedo, averaged annually (ANN), in summer (JJA), and winter (DJF). Dotted areas are where differences are not statistically significant at 95% confidence interval. Each panel shows differences between COOL and DARK cases.
Download figure:
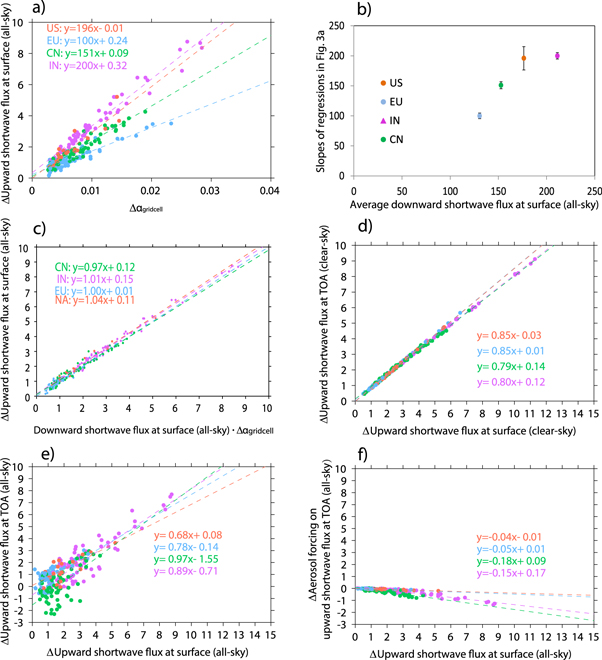
Standard image High-resolution image
Figure 3. Scatter plots showing changes (COOL minus DARK) in (a) all-sky (i.e. including clouds) upward shortwave flux (W m−2) at the surface versus Δαgridcell, (b) see below, (c) all-sky upward shortwave flux at the surface versus the product of insolation at the surface and Δαgridcell in DARK case, (d) clear-sky (i.e. no cloud) upward shortwave flux at the top of the atmosphere versus changes in clear-sky upward shortwave flux at the surface, (e) all-sky upward shortwave flux at the top of the atmosphere versus changes in all-sky upward shortwave flux at the surface, and (f) shortwave aerosol forcing at the top of the atmosphere versus changes in all-sky upward shortwave flux at the surface. Each dot represents a different model grid cell. Colors denote different continental-scale regions: the United States, China, India, and Europe, which are represented by 20, 66, 65, and 81 grid cells, respectively. Dashed lines denote best fit linear regressions derived using least squares for each region. Aerosol forcing refers to the difference in outgoing solar radiation at the top of the atmosphere in the presence and absence of aerosols. A scatter plot for the slopes of regressions in figure 3(a) versus average downward shortwave flux at the surface in the four continental-scale regions in DARK case is shown in (b). Each point represents a different region in this panel, and 1-sigma uncertainties in the slopes are included.
Download figure:
Standard image High-resolution image3.2. The influence of cool roofs on continental-scale energy fluxes and climate
Figure 3 depicts the impacts of cool roofs on energy fluxes averaged over our four continental-scale regions of analysis (see figure 1(b)). Recall that only grid cells with 
greater than 0.004 are included in the analyses presented here (see section 2.3). Also note that the grid cells are comprised of both urban and rural areas.
For each region, increasing 
proportionally enhances the solar radiation reflected by the surface (figure 3(a)). As shown by the slopes of the best fit lines in figure 3(a), reflected solar radiation appears more sensitive to 
for regions at low-latitudes and with lower baseline cloudiness, both of which tend to increase incoming solar radiation. Figures 3(b) and (c) show that the change in reflected solar radiation approximates to the product of 
and incoming solar radiation at the surface, causing the slopes in figure 3(a) to be correlated to incoming solar radiation. Under clear-sky (i.e. no cloud) conditions, the increase in solar radiation reflected by the surface from cool roofs leads to proportional increases in outgoing solar radiation at the top of the atmosphere (figure 3(d)) in each of the four regions. The sensitivity of outgoing solar radiation at the top of atmosphere versus upward radiation at the surface, as diagnosed using the slope of the best fit lines in figure 3(d), is similar among the regions. Considering all-sky (i.e. with clouds) conditions (figure 3(e)) rather than clear-sky conditions (figure 3(d)) leads to more variation among regions in the aforementioned sensitivity. This is likely caused by differences among regions in baseline cloud cover, which affects the fraction of upward solar radiation at the surface that escapes to space. Similarly, there is more variability within each region in the all-sky case, a consequence of natural variability in simulated cloud cover between each ensemble member for the COOL and DARK cases. Variations in clouds strongly influence energy transfer from the surface to the top of the atmosphere, and in some cases can outweigh the influence of increasing roof albedo.
Aerosols are expected to decrease the radiative benefits of cool roofs by absorbing upwelling solar radiation, and reflecting upwelling radiation back to the surface (Jacobson and Ten Hoeve 2012, Millstein and Fischer 2014). However, this effect has never been quantified using a three-dimensional atmosphere model, and has not been computed either at larger than urban scales or in different countries. Aerosol forcing (i.e. the difference in outgoing solar radiation at the top of the atmosphere in the presence versus absence of aerosols) can quantify the influence of aerosols on energy transmitted through the atmosphere. As shown in figure 3(f), aerosol forcing becomes more negative as reflected solar radiation at the surface from cool roofs increases. This suggests that in the presence of aerosols, less energy reflected by the surface escapes to space. The slope of the best fit line for △aerosol forcing versus △reflected solar radiation varies from −0.04 in the United States to −0.18 in more polluted China (figure 3(f)), suggesting that aerosols offset 4%–18% of the radiative benefits of cool roofs. As shown in table S1, AOD in China and the United States represent the maximum (0.21) and the minimum (0.10) among the four regions, and correspond to the maximum and the minimum changes in aerosol forcing. It should be noted that the impact of aerosols on the radiative benefits of cool roofs are studied on continental scale, but not on the subgrid urban scale. Urban aerosol levels are expected to be higher than grid cell average levels, and therefore aerosols are likely to intercept a larger absolute amount of radiation reflected by the surface over cities. However, since absolute amounts of reflected radiation are also higher within urban areas relative to grid cell averages, the overall sensitivity (i.e. slope in figure 3(f)) should remain the same whether computed using gridcell or subpixel urban values.
Table 1 summarizes temperature changes from cool roof adoption in the four continental-scale regions. Note that the values reported are grid cell averages including both urban and nonurban portions of the cell. There are statistically significant decreases in annual mean surface air temperatures in the United States (0.11 ± 0.10 K) and China (0.14 ± 0.12 K). Temperature changes in India and Europe are statistically indistinguishable from zero (−0.08 ± 0.12 K and 0.07 ± 0.15 K, respectively). Thus, adoption of cool roofs is likely to reduce surface air temperatures in China and the United States, while its impacts in Europe and India appear smaller than natural climate variability when changes are computed at continental-scale.
Table 1.
30 year mean surface air temperatures averaged over four continental-scale regions (see figure 1(b)) for the DARK case, and differences between the COOL and DARK cases. Uncertainties are quantified using the Student's t-test at 95% confidence level. Only grid cells with 
are included in these continental-scale averages. Values represent grid cell averages including both the urban and non-urban portions of the cell.
| Region | DARK | COOL–DARK | |
|---|---|---|---|
| 2 m air temperature (K) | US | 287.7 | −0.11 ± 0.10 |
| China | 287.8 | −0.14 ± 0.12 | |
| India | 299.4 | −0.08 ± 0.12 | |
| Europe | 284.8 | 0.07 ± 0.15 |
3.3. The influence of cool roofs on global energy fluxes and climate
Table 2 summarizes the impacts of cool roofs (COOL minus DARK) on global mean temperatures, energy fluxes, and hydrological variables. Note that global averages include all grid cells, not just those with 
as in the previous section. The difference in global- and annual-mean surface air temperature between COOL versus DARK is −0.0021 K, with a 95% confidence interval of −0.028 to +0.024 K. Previous studies disagree on the global climate impacts of cool roofs. Akbari et al (2012) suggest that increasing urban albedo by 0.1 globally would reduce global average temperatures by 0.01 or 0.07 K, based on two different datasets of urban area respectively. On the other hand, Jacobson and Ten Hoeve (2012) suggest that cool roofs would warm the globe by 0.07 K. Uncertainty estimates for global average temperature changes are not provided by these studies. Based on a suite of ensemble simulations to estimate uncertainty, our results suggest that although cool roofs might exert a cooling effect (0.002 K) on global climate, the cooling is smaller than the uncertainty from natural variability.
Table 2. 30 year globally averaged temperatures, albedo, energy fluxes, and hydrologic variables for the DARK case, and differences between the DARK and COOL cases. Uncertainties are quantified using the Student's t-test at 95% confidence level. Unlike the continental-scale means (table 1), all grid cells are included in these averages.
| Variables | DARK | COOL–DARK |
|---|---|---|
| Ground temperature (K) | 289.6 | −0.0013 ± 0.026 |
| Surface air temperature (K) | 288.8 | −0.0021 ± 0.026 |
| Albedo (shortwave, direct)a | 0.57 | 0.00029 ± 0.00009 |
| Albedo (shortwave, diffuse)a | 0.55 | 0.00028 ± 0.00009 |
| Net solar flux at surface (W m−2)b | 160.8 | −0.042 ± 0.084 |
| Net solar flux at top of model (W m−2)b | 237.3 | −0.053 ± 0.079 |
| Net longwave flux at surface (W m−2)c | 52.3 | 0.053 ± 0.049 |
| Net longwave flux at top of model (W m−2)c | 237.4 | −0.041 ± 0.073 |
| Surface latent heat flux (W m−2)c | 90.9 | −0.075 ± 0.085 |
| Surface sensible heat flux (W m−2)c | 17.1 | −0.005 ± 0.031 |
| Precipitation rate (m s−1) | 1.0 × 10−8 | −3.0 × 10−11 ± 4.7 × 10−11 |
| Water equivalent snow depth (m) | 3.8 × 10−2 | 9.9 × 10−5 ± 6.9 × 10−5 |
| 2 m humidity (kg kg−1) | 0.011 | −1.4 × 10−5 ± 1.7 × 10−5 |
| Column precipitable water (kg m−2) | 28.13 | −0.046 ± 0.050 |
| Low cloud fraction | 0.42 | −7.2 × 10−4 ± 5.4 × 10−4 |
| Mid-level cloud fraction | 0.26 | 2.0 × 10−4 ± 3.1 × 10−4 |
| High cloud fraction | 0.38 | 7.0 × 10−4 ± 5.0 × 10−4 |
aAlbedo is output by the simulations including feedbacks, as opposed to 
which is the change we imposed in the input file.
bFluxes are positive downward.
cFluxes are positive upward.
Our simulations suggest that global adoption of cool roofs cause statistically insignificant decreases in surface ground and air temperatures, and precipitation (table 2). As discussed in previous research (Georgescu et al 2012, 2014, Jacobson and Ten Hoeve 2012), decreasing surface air temperature can in some cases suppress convection to the point that precipitation is reduced. Increases in global average surface albedo, including both adoption of cool roofs and feedbacks in snow and ice, are statistically significant (0.0003 ± 0.000 09), while decreases in the downward positive net solar flux at the surface (−0.042 ± 0.084) and at the top of the model (−0.053 ± 0.079) are statistically insignificant. Adoption of cool roofs leads to global mean low cloud fraction (>700 hPa) decreases of 0.02% ± 0.13%, mid-level (400–700 hPa) cloud fraction increases of 0.08% ± 0.12%, and high (<400 hPa) cloud fraction increases of 0.02% ± 0.13%. Increasing snow depth (0.26% ± 0.18%) may be a feedback from lower surface air temperatures. It should be noted that all the global changes listed in table 2 except changes in surface albedo and snow depth are statistically insignificant, meaning most changes induced by cool roofs are smaller than the natural variability on global scale.
4. Discussion
Previous studies have quantified the equivalent CO2 offset from cool roof adoption by comparing changes in the TOA radiation balance from cool roofs to changes in radiative forcing from CO2 increases (Akbari et al 2009, Menon et al 2010, Millstein and Menon 2011, Millstein and Fischer 2014). Radiative forcing is the change in downward positive radiative flux at the top of the atmosphere after introducing a forcing agent, and was originally developed as an effective framework to evaluate and compare the climate impacts of various greenhouse gases (IPCC 2013). Note that there are many different methods for calculating radiative forcings of climate change agents (Hansen et al 1997, 2005).
Greenhouse gases are mostly well-mixed in the atmosphere and warm the Earth by reducing the amount of longwave radiation that escapes the Earth system to space. Thus, radiative forcing from different greenhouse gases (e.g. carbon dioxide, methane, nitrous oxide) lead to climate responses via similar physical mechanisms, and likewise have similar climate sensitivity parameters (i.e. the ratio of global mean surface air temperature response to radiative forcing). Though radiative forcing can be an effective framework for comparing the effects of greenhouse gases on global temperatures, other radiative forcing agents that are not globally well mixed, or alter the shortwave rather than longwave energy budget, may not fit into the same framework as well due to differences in climate sensitivity parameter (Hansen et al 2005, Ban-Weiss et al 2012). Black carbon particles, which are globally heterogeneous (Zhang et al 2015), and absorb shortwave rather than longwave radiation, are a prime example. The climate sensitivity of black carbon particles at different altitudes can range from 61% lower to 25% higher than the climate sensitivity of CO2 (Ban-Weiss et al 2012). This suggests that equivalent radiative forcings from CO2 and black carbon are expected to cause vastly different global temperature impacts. The same logic applies to cool roofs as the climate sensitivity parameters of CO2 and cool roofs are likely to be different given that the latter changes the planetary shortwave radiation budget while the former changes the longwave radiation budget. Additionally, cool roofs are concentrated in urban regions and are therefore highly globally heterogeneous. Therefore, we suggest that making the equivalence between CO2 and cool roofs in terms of radiative forcing may be less meaningful than desired, especially if comparing their impacts on global temperature is sought after. Rather than reporting this equivalence in the present research, we investigate the potential global climate impacts of cool roofs using simulations from an Earth system model.
Although the impacts of cool roofs on radiative forcing can be suggestive of their climate impacts, the climate response (i.e. including feedbacks) to the radiative forcing determines their climate consequences. Only two previous studies have calculated equivalent CO2 reductions corresponding to cool roof adoption based on their global temperature impacts (as opposed to radiative forcing impacts); Akbari et al (2012) and Akbari and Matthews (2012) report that increasing urban albedo by 0.1 is equivalent to one-time CO2 emission reductions of 25–150 Gt and 160 Gt CO2, respectively. Note, however, that the atmospheric model they use is a two-dimensional energy and moisture balance model that does not consider atmospheric aerosol and cloud feedbacks. Employing a coupled Earth system model can simulate atmospheric feedback processes and therefore is important for furthering understanding of the climate impacts of cool roofs on large scales. Using such a model, we find that cool roofs significantly reduce temperatures in most cities around the globe. The impacts of cool roofs at the continental-scale are more uncertain given that urban regions make up a smaller fraction of the total area. Surface air temperature decreases are statistically significant in the United States and China, but insignificant in India; there is a statistically insignificant surface air temperature increase in Europe. Cool roofs are found to reduce global average surface air temperatures, but the temperature change is not statistically significant since its effect is smaller than natural variability.
It should be noted that we have only assessed the impacts of cool roofs as an approach to reduce absorbed solar radiation by the Earth system. Cool roofs can also indirectly influence the climate by reducing heat transferred into buildings, decreasing air conditioning energy use, and reducing greenhouse gas emissions associated with energy production (Levinson and Akbari 2010, Gao et al 2014). In addition, as with any research using models, the results presented here may be model dependent and should be further corroborated using other Earth system models. Lastly, our model is run at a coarse resolution (1.9° × 2.5°). The magnitude of modeled atmospheric feedbacks may be dependent on spatial resolution. For example, aerosol-cloud interactions can be better simulated in climate models at higher model resolution (Ma et al 2014). When computationally feasible, future work should repeat this study using a global climate model at a higher resolution (e.g. ¼°).
5. Conclusion
In this study, we use the CESM to investigate the impacts of deploying cool roofs in urban regions around the globe on urban, continental-scale, and global climate. We find that increasing roof albedo from 0.15 to 0.90 reduces urban heat islands (i.e. urban minus rural air temperature) everywhere. The decreases are statistically significant, except in some areas in Africa and Mexico where urban fraction is low, and some high-latitude areas during wintertime. The annual- and global-mean urban heat island decreases from 1.6 to 1.2 K.
We analyze the impacts of cool roofs at the continental-scale in four areas: United States, China, India, and Europe. For each region, the solar radiation reflected by the Earth surface increases proportionally to the estimated surface albedo increase, as expected. For clear-sky (i.e. cloud free) conditions, the increase in reflected solar radiation at the surface proportionally enhances outgoing shortwave radiation at the top of atmosphere, suggesting a radiative cooling effect of cool roofs. However, for all-sky (i.e. with clouds) conditions, the influence of natural climate variability especially from changes in cloud cover on the energy balance at the top of the atmosphere in some cases outweighs the influence of cool roofs. Aerosols have been hypothesized to partially offset the effects of cool roofs by directly absorbing upwelling solar radiation, and reflecting upwelling radiation back to the surface. However, the magnitude of this effect has never been quantified using an Earth system model. We find that the additional aerosol forcing induced by cool roofs is 4%–18% of the increase in reflected solar radiation at the surface; regions with higher AOD are shown to absorb more reflected upward radiation than those with lower AOD. With cool roofs, annual mean surface air temperatures in the United States and China show statistically significant decreases of 0.11 ± 0.10 K and 0.14 ± 0.12 K, respectively, while in Europe and India the mean surface air temperature changes are statistically insignificant.
Past studies disagree on the influence of cool roofs on global climate. Some studies suggest that implementing cool roofs in cities around the globe would lead to global cooling (Akbari et al 2009, 2012, Akbari and Matthews 2012), while another study (Jacobson and Ten Hoeve 2012) suggests that cool roofs could cause the globe to warm. The research presented here indicates that adoption of cool roofs around the globe would lead to statistically insignificant reductions in global mean air temperature (−0.0021 ± 0.026 K). Thus, we suggest that while cool roofs are an effective tool for reducing building energy use in hot climates, urban heat islands, and regional air temperatures, their influence on global climate is likely negligible.
Acknowledgments
This research was supported by the National Science Foundation under grant CBET-1512429. A portion of the computation for the work described in this paper was supported by the University of Southern California's Center for High-Performance Computing (hpc.usc.edu). We thank Pouya Vahmani, Arash Mohegh, Trevor Krasowsky, Mohammad Taleghani, Jing Meng, Yan Xia, and Wei Tao for their helpful suggestions. Computational resources at the Pacific Northwest National Laboratory were provided by the PNNL Institutional Computing (PIC). Kai Zhang was supported by the Office of Science of US Department of Energy as part of the Earth System Modeling Program. The Pacific Northwest National Laboratory is operated for DOE by Battelle Memorial Institute under contract DE-AC06-76RLO 1830.