эО╕эММ(эММ)
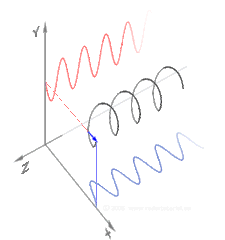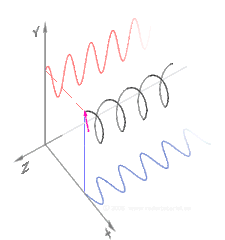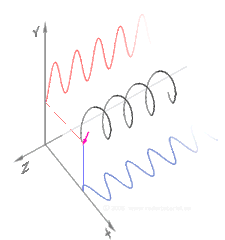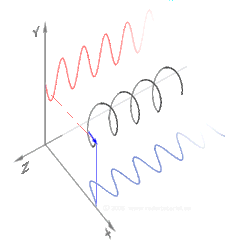
Polarization (waves)эО╕эММ(эО╕эММыПД)ыКФ [1][2][3][4][5]ьзДыПЩьЭШ ъ╕░эХШэХЩьаБ ы░йэЦеьЭД ьзАьаХэХШыКФ эЪбэММьЧР ьаБьЪйыРШыКФ эК╣ьД▒ьЮЕыЛИыЛд.эЪбэММьЧРьДЬ ьзДыПЩ ы░йэЦеьЭА [4]эММыПЩьЭШ ьЪ┤ыПЩ ы░йэЦеъ│╝ ьИШьзБьЭ┤ыЛд.эО╕ъ┤С эЪбэММьЭШ ъ░ДыЛиэХЬ ьШИыбЬыКФ эМ╜эМ╜эХЬ ьдДьЭД ыФ░ыЭ╝ ьЭ┤ыПЩэХШыКФ ьзДыПЩ(ьЭ┤ып╕ьзА ь░╕ьб░)ьЭ┤ ьЮИьК╡ыЛИыЛд. ьШИые╝ ыУдьЦ┤ ъ╕░эГА эШДъ│╝ ъ░ЩьЭА ьХЕъ╕░ьЮЕыЛИыЛд.эШДьЭ┤ ьЦ┤ыЦ╗ъ▓М ы╜СэЮИыКРыГРьЧР ыФ░ыЭ╝ ьзДыПЩьЭ┤ ьИШьзБ ы░йэЦе, ьИШэПЙ ы░йэЦе ыШРыКФ эШДьЧР ьИШьзБьЭ╕ ьЮДьЭШьЭШ ъ░БыПДыбЬ ы░ЬьГЭэХа ьИШ ьЮИьК╡ыЛИыЛд.ы░Шый┤ ьХбь▓┤ыВШ ъ╕░ь▓┤ ьдС ьЭМэММ ыУ▒ ьвЕэММьЧРьДЬыКФ ьзДыПЩ ыВ┤ ьЮЕьЮРьЭШ ы│АьЬДыКФ эХньГБ ьаДэММы░йэЦеьЭ┤ъ╕░ ыХМым╕ьЧР эО╕эММ эШДьГБьЭ┤ ыВШэГАыВШьзА ьХКыКФыЛд.эО╕эММ эШДьГБьЭД ы│┤ьЭ┤ыКФ ъ░АыбЬэММьЧРыКФ ы╣Ыъ│╝ ьаДэММ ыУ▒ ьаДьЮРэММ, ьдСыаеэММ,[6] ъ│аь▓┤ ьдСьЭШ ъ░АыбЬьЭМэММ(ьаДыЛиэММ) ыУ▒ьЭ┤ ьЮИыЛд.
ы╣Ыъ│╝ ъ░ЩьЭА ьаДьЮРэММыКФ эХньГБ ьДЬыбЬ ьИШьзБьЭ╕ ъ▓░эХйыРЬ ьзДыПЩ ьаДъ│ДьЩА ьЮРъ╕░ьЮеьЬ╝ыбЬ ъ╡мьД▒ыРШьЦ┤ ьЮИьЬ╝ый░, ъ┤АыбАьГБ ьаДьЮРэММьЭШ "эО╕эММ"ыКФ ьаДъ│ДьЭШ ы░йэЦеьЭД ызРэХЬыЛд.ьДаэШХ эО╕эММьЧРьДЬыКФ эХДыУЬъ░А ыЛиы░йэЦеьЬ╝ыбЬ ьзДыПЩэХйыЛИыЛд.ьЫРэШХ ыШРыКФ эГАьЫР эО╕ъ┤СьЧРьДЬыКФ эММэШХьЭ┤ ьЭ┤ыПЩэХа ыХМ эПЙый┤ьЧРьДЬ эХДыУЬъ░А ьЭ╝ьаХэХЬ ьЖНыПДыбЬ эЪМьаДэХйыЛИыЛд.эЪМьаДьЧРыКФ ыСР ъ░АьзА ы░йэЦеьЭ┤ ьЮИьЭД ьИШ ьЮИьК╡ыЛИыЛд. эММыПЩ ьЭ┤ыПЩ ы░йэЦеьЧР ыМАэХ┤ эХДыУЬъ░А ьЪ░ь╕бьЬ╝ыбЬ эЪМьаДэХШыКФ ъ▓╜ьЪ░ ьЪ░ь╕б ьЫРэШХ эО╕эММыЭ╝ъ│а эХШый░, эХДыУЬъ░А ьвМь╕бьЬ╝ыбЬ эЪМьаДэХШыКФ ъ▓╜ьЪ░ ьвМь╕б ьЫРэШХ эО╕эММыЭ╝ъ│а эХйыЛИыЛд.
эГЬьЦС, ы╢Иъ╜Г, ы░▒ьЧ┤ыУ▒ъ│╝ ъ░ЩьЭА ызОьЭА ъ┤СьЫРьЬ╝ыбЬы╢АэД░ьЭШ ы╣ЫьЭ┤ыВШ ыЛдые╕ ьаДьЮРъ╕░ ы░йьВмьДаьЭА эО╕ъ┤СьЭШ ыПЩьЭ╝эХЬ эШ╝эХйьЭД ъ░АьзД ыЛиэММьЧ┤ыбЬ ъ╡мьД▒ыРШьЦ┤ ьЮИыЛд. ьЭ┤ъ▓ГьЭА эО╕ъ┤СыРШьзА ьХКьЭА ы╣ЫьЭ┤ыЭ╝ъ│а ы╢Иыж░ыЛд.эО╕ъ┤СьЭА эО╕ъ┤СьЮРые╝ эЖ╡эХ┤ ы╣ДэО╕ъ┤СьЭШ эЖ╡ъ│╝ые╝ эЖ╡эХ┤ ьГЭьД▒ыРа ьИШ ьЮИьЬ╝ый░, эО╕ъ┤СьЮРыКФ эО╕ъ┤СьЮРъ░А эХШыВШызМ эЖ╡ъ│╝эХа ьИШ ьЮИьК╡ыЛИыЛд.ъ░АьЮе ьЭ╝ы░ШьаБьЭ╕ ъ┤СэХЩ ьЮмыгМыКФ ы╣ЫьЭШ эО╕ъ┤СьЧР ьШБэЦеьЭД ып╕ь╣ШьзА ьХКьзАызМ ы│╡ъ╡┤ьаИ, ьЭ┤ьГЙьД▒ ыШРыКФ ъ┤СэХЩ эЩЬыПЩьЭД ы│┤ьЭ┤ыКФ ьЮмыгМыКФ эО╕ъ┤СьЧР ыФ░ыЭ╝ ыЛдые┤ъ▓М ы╣ЫьЧР ьШБэЦеьЭД ып╕ь╣йыЛИыЛд.ьЭ┤ ьдС ьЭ╝ы╢АыКФ эО╕ъ┤С эХДэД░ые╝ ызМыУЬыКФ ыН░ ьВмьЪйыРйыЛИыЛд.ы╣ЫьЭА ыШРэХЬ эСЬый┤ьЧРьДЬ ы╣ДьКдыУмэЮИ ы░ШьВмыРа ыХМ ы╢Аы╢ДьаБьЬ╝ыбЬ эО╕ъ┤СыРйыЛИыЛд.
ьЦСьЮРьЧнэХЩьЧР ыФ░ые┤ый┤ ьаДьЮРэММыКФ ъ┤СьЮРыЭ╝ъ│а ы╢ИыжмыКФ ьЮЕьЮРьЭШ эЭРыжДьЬ╝ыбЬыПД ы│╝ ьИШ ьЮИыЛд.ьЭ┤ыаЗъ▓М ы│╝ ыХМ, ьаДьЮРэММьЭШ эО╕ъ┤СьЭА [7][8]ьКдэХАьЭ┤ыЭ╝ъ│а ы╢ИыжмыКФ ъ┤СьЮРьЭШ ьЦСьЮР ьЧнэХЩьаБ эК╣ьД▒ьЧР ьЭШэХ┤ ъ▓░ьаХыРйыЛИыЛд.ъ┤СьЮРыКФ ыСР ъ░АьзА ъ░АыКеэХЬ ьКдэХА ьдС эХШыВШые╝ ъ░АьзАъ│а ьЮИыЛд: ъ┤СьЮРыКФ ьЭ┤ыПЩ ы░йэЦеьЧР ыМАэХ┤ ьШдые╕ьЖР ъ░Ръ░Б ыШРыКФ ьЩ╝ьЖР ъ░Ръ░БьЬ╝ыбЬ эЪМьаДэХа ьИШ ьЮИыЛд.ьЫРэО╕ъ┤С ьаДьЮРэММыКФ ьШдые╕ьк╜ ыШРыКФ ьЩ╝ьк╜ьЭШ эХЬ ъ░АьзА ьЬаэШХьЭШ ьКдэХАызМьЭД ъ░АьзД ъ┤СьЮРыбЬ ъ╡мьД▒ыРйыЛИыЛд.ьзБьДа эО╕эММыКФ ьвМьЪ░ ьЫРэО╕ъ┤С ьГБэГЬьЭШ ьдСь▓й ьЬДь╣ШьЧР ьЮИыКФ ъ┤СьЮРыбЬ ъ╡мьД▒ыРШый░,[8] эПЙый┤ьЧРьДЬ ьзДыПЩьЭД ьг╝ъ╕░ ьЬДэХ┤ ыПЩьЭ╝эХЬ ьзДэПнъ│╝ ьЬДьГБьЭ┤ ыПЩъ╕░эЩФыРйыЛИыЛд.
эО╕ъ┤СьЭА ъ┤СэХЩ, ьзАьзДэХЩ, ьаДэММ, ызИьЭ┤эБмыбЬэММ ыУ▒ эЪбэММые╝ ыЛдыгиыКФ ъ│╝эХЩ ы╢ДьХ╝ьЧРьДЬ ьдСьЪФэХЬ ы│АьИШьЭ┤ыЛд.эК╣эЮИ ьШБэЦеьЭД ы░ЫыКФ ъ▓ГьЭА ыаИьЭ┤ьаА, ым┤ьДа ы░П ъ┤СьДмьЬа эЖ╡ьЛа, ыаИьЭ┤ыНФ ыУ▒ьЭШ эЕМэБмыЖАыбЬьзАьЮЕыЛИыЛд.
ьДЬыба
эММыПЩ ьаДэММ ы░П эО╕эММ
ыМАы╢Аы╢ДьЭШ ъ┤СьЫРьЭА ъ│╡ъ░Д эК╣ьД▒, ьг╝эММьИШ(эММьЮе), ьЬДьГБ ы░П эО╕ъ┤С ьГБэГЬъ░А ыЛдые╕ ьЮДьЭШ эШ╝эХй эММьЮеьЬ╝ыбЬ ъ╡мьД▒ыРШъ╕░ ыХМым╕ьЧР ьЭ╝ъ┤АьД▒ьЭ┤ ьЧЖъ│а эО╕ъ┤СыРШьзА ьХКьЭА(ыШРыКФ "ы╢Аы╢Д эО╕ъ┤С"ызМ) ъ▓ГьЬ╝ыбЬ ы╢ДыеШыРйыЛИыЛд.ыЛи, ьаДьЮРэММьЩА эО╕эММые╝ ьЭ┤эХ┤эХШъ╕░ ьЬДэХ┤ьДЬыКФ ъ░ДьДньД▒ эПЙый┤эММые╝ ъ│аыадэХШыКФ ъ▓ГьЭ┤ ыНФ ьЙ╜ьК╡ыЛИыЛд.ьЭ┤ъ▓ГьЭА эК╣ьаХ ы░йэЦе(ыШРыКФ эММы▓бэД░), ьг╝эММьИШ, ьЬДьГБ ы░П эО╕эММ ьГБэГЬьЭШ ьВмьЭ╕эММьЮЕыЛИыЛд.эК╣ьаХ ъ│╡ъ░Дъ╡мьб░ые╝ ъ░АьзД эММэШХьЭА эПЙый┤эММ(ьЭ┤ые╕ы░Ф ъ░БыПД ьКдэОЩэК╕ыЯ╝)ьЭШ ьб░эХйьЬ╝ыбЬ ы╢ДэХ┤ыРа ьИШ ьЮИъ╕░ ыХМым╕ьЧР эПЙый┤эММьЧР ъ┤АэХЬ ъ┤СэХЩъ│ДьЭШ эК╣ьД▒эЩФые╝ ьВмьЪйэХШьЧм ы│┤ыЛд ьЭ╝ы░ШьаБьЭ╕ ъ▓╜ьЪ░ьЧР ыМАэХЬ ьЭСыЛ╡ьЭД ьШИь╕бэХа ьИШ ьЮИыЛд.ы╣ДьЭ╝ъ┤АьД▒ ьГБэГЬыКФ ьг╝эММьИШ(ьКдэОЩэК╕ыЯ╝), ьЬДьГБ ы░П эО╕ъ┤СьЭШ ы╢ДэПмьЩА ьГБъ┤АьЧЖыКФ эММэШХьЭШ ъ░АьдС ьб░эХйьЬ╝ыбЬ эЩХыеаьаБьЬ╝ыбЬ ыкиыН╕ызБэХа ьИШ ьЮИыЛд.
ъ░АыбЬ ьаДьЮРэММ
ьЮРьЬа ъ│╡ъ░Д ыШРыКФ ыЛдые╕ ъ╖аьзИ ыУ▒ы░йьД▒ ы╣Дъ░РьЗа ыздь▓┤ые╝ ьЭ┤ыПЩэХШыКФ ьаДьЮРэММ(ьШИые╝ ыУдьЦ┤ ы╣Ы)ыКФ эЪбэММыбЬ ьаБьаИэХШъ▓М ьДдыкЕыРШый░, ьЭ┤ыКФ эПЙый┤эММьЭШ ьаДъ│Д ы▓бэД░ EьЩА ьЮРъ╕░ьЮе Hъ░А ъ░Бъ░Б эММыПЩ ьаДэММ ы░йэЦеьЧР ьИШьзБ(ыШРыКФ "эЪб")ьЭ╕(ыШРыКФ "эЪб") ы░йэЦеьЮДьЭД ьЭШып╕эХЬыЛд. EьЩА HыКФ эММыПЩ ьаДэММ ы░йэЦеьЭ┤ыЛд.lsoыКФ ьДЬыбЬ ьИШьзБьЭ┤ыЛд.ъ┤АыбАьГБ ьаДьЮРэММьЭШ 'эО╕эММ' ы░йэЦеьЭА ъ╖╕ ьаДъ│Д ы▓бэД░ьЧР ьЭШэХ┤ ьг╝ьЦ┤ьзДыЛд.ъ┤Сьг╝эММьИШ fьЭШ ыЛиьГЙ эПЙый┤эММ(ьзДъ│╡эММьЮе ╬╕ьЭШ ы╣ЫьЭА f = c/colm, ьЧмъ╕░ьДЬ cыКФ ы╣ЫьЭШ ьЖНыПД)ые╝ ъ│аыадэХШьЧм ьаДэММ ы░йэЦеьЭД zь╢ХьЬ╝ыбЬ эХЬыЛд.Ez = Hz = 0. ы│╡ьЮбэХЬ(ыШРыКФ ыЛиъ│ДьаБ) эСЬъ╕░ы▓ХьЭД ьВмьЪйэХШьЧм ьИЬъ░Д ым╝ыжм ьаДъ╕░ьЮеъ│╝ ьЮРъ╕░ьЮеьЭА ыЛдьЭМ ы░йьаХьЛЭьЧРьДЬ ы░ЬьГЭэХШыКФ ы│╡ьЮбэХЬ ьЦСьЭШ ьЛдьаЬ ы╢Аы╢ДьЧР ьЭШэХ┤ ьг╝ьЦ┤ьзДыЛд.ьЛЬъ░Д t ы░П ъ│╡ъ░Д ьЬДь╣Ш zьЭШ эХиьИШыбЬьДЬ(+z ы░йэЦеьЭШ эПЙый┤эММьЭШ ъ▓╜ьЪ░ эХДыУЬъ░А x ыШРыКФ yьЧР ьЭШьб┤эХШьзА ьХКьЬ╝ыпАыбЬ) ьЭ┤ыЯмэХЬ ы│╡ьЮбэХЬ эХДыУЬыКФ ыЛдьЭМъ│╝ ъ░ЩьЭ┤ ьУ╕ ьИШ ьЮИьК╡ыЛИыЛд.
ъ╖╕ыжмъ│а.
ьЧмъ╕░ьДЬ ╬┤ = ╬┤0/nьЭА ыздьзИ ыВ┤ьЭШ эММьЮе(ъ╡┤ьаИыеаьЭА n), T = 1/fыКФ эММыПЩьЭШ ьг╝ъ╕░ьЭ┤ыЛд.ьЧмъ╕░ьДЬx e, ey, hx, hыКФy ы│╡ьЖМьИШьЮЕыЛИыЛд.ы│┤ыЛд ь╜дэМйэК╕эХЬ ыСР ы▓Иьз╕ эШХэГЬьЧРьДЬыКФ ьЭ┤ыУд ы░йьаХьЛЭьЭ┤ ъ┤АьК╡ьаБьЬ╝ыбЬ эСЬэШДыРа ыХМ, ьЭ┤ыЯмэХЬ ьЭ╕ьЮРыКФ эММьИШ / 0 {{ k n _ ы░П ъ░Б ьг╝эММьИШ(ыШРыКФ "ыЭ╝ыФФьХИ ьг╝эММьИШ") f { fые╝ ьВмьЪйэХШьЧм ы│┤ыЛд ьЭ╝ы░ШьаБьЭ╕ ьаДэММые╝ ьВмьЪйэХШьЧм ьДдыкЕыРЬыЛд.+z ы░йэЦеьЬ╝ыбЬ ьЭ┤ыПЩэХШый┤ ъ│╡ъ░Д ьЭШьб┤ьД▒ kzъ░А k {ot {r}ыбЬ ыРйыЛИыЛд. ьДЬ k {\{k}}ьЭА эММыПЩ ы▓бэД░(\displaystyle {ыЭ╝ъ│а эХШый░, ъ╖╕ эБмъ╕░ыКФ эММыПЩ ы▓бэД░ьЮЕыЛИыЛд.
ыФ░ыЭ╝ьДЬ ьДаэЦЙ ы▓бэД░ eьЩА hыКФ ъ░Бъ░Б эММэШХьЭШ x ы░П y эО╕эММ ьД▒ы╢ДьЭШ ьзДэПнъ│╝ ьЬДьГБьЭД ьДдыкЕэХШыКФ ь╡ЬыМА 2ъ░ЬьЭШ 0ьЭ┤ ьХДыЛМ(ы│╡ьЮбэХЬ) ьД▒ы╢ДьЭД эПмэХиэХйыЛИыЛд(ыШРэХЬ +z ы░йэЦеьЭШ эЪбэММьЧР ыМАэХЬ z эО╕эММ ьД▒ы╢ДьЭА ьб┤ьЮмэХа ьИШ ьЧЖьК╡ыЛИыЛд).эК╣ьД▒ ьЮДэФ╝ыНШьКд {\ые╝ ъ░ЦыКФ эК╣ьаХ ыздь▓┤ьЧР ыМАэХ┤ hыКФ ыЛдьЭМъ│╝ ъ░ЩьЭ┤ eьЩА ъ┤АыаиыРйыЛИыЛд.
ъ╖╕ыжмъ│а.
- x - y {\{}=-{\
ьЬаьаДь▓┤ьЧРьДЬ ╬╕ыКФ ьЛдьЮмэХШъ│а ъ░Т ╬╕0/nьЭД ъ░АьзДыЛд.ьЧмъ╕░ьДЬ nьЭА ъ╡┤ьаИыеа, ╬╕ыКФ0 ьЮРьЬаъ│╡ъ░ДьЭШ ьЮДэФ╝ыНШьКдьЭ┤ыЛд.ьаДыПД ыздь▓┤ьЧРьДЬыКФ ьЮДэФ╝ыНШьКдъ░А ы│╡ьЮбэХ┤ьзСыЛИыЛд.[clarification needed]ьЭ┤ ъ┤Аъ│Дые╝ ъ│аыадэХа ыХМ EьЩА HьЭШ ыПДэК╕ъ│▒ьЭА [dubious ]0ьЭ┤ьЦ┤ьХ╝ эХйыЛИыЛд.
ьЭ┤ыЯмэХЬ ы▓бэД░ъ░А ьШИьГБыМАыбЬ ьзБъ╡Р(ьДЬыбЬ ьзБъ░Б)ьЮДьЭД ыВШэГАыГЕыЛИыЛд.
ыФ░ыЭ╝ьДЬ ьаДэММ ы░йэЦе(+z)ъ│╝ ╬╕ые╝ ьХМый┤ ьаДъ│Дые╝ ыВШэГАыВ┤ыКФ eьЩАx eыбЬy эММэШХьЭД ьзАьаХэХа ьИШ ьЮИьК╡ыЛИыЛд.eьЩАy eые╝ эПмэХиэХШыКФx ы▓бэД░(ыЛи, ъ░АыбЬэММьЭШ ъ▓╜ьЪ░ ы░ШыУЬьЛЬ 0ьЭ╕ z ьД▒ы╢ДьЭ┤ ьЧЖьЭМ)ые╝ ьб┤ьКд ы▓бэД░ыЭ╝ъ│а эХйыЛИыЛд.эММэШХьЭШ эО╕ъ┤С ьГБэГЬые╝ ьзАьаХэХШыКФ ъ▓Г ьЩ╕ьЧР ьЭ╝ы░Ш Jones ы▓бэД░ыКФ эММэШХьЭШ ьаДь▓┤ ъ╖ЬыкиьЩА ьЬДьГБьЭД ъ╖ЬьаХэХйыЛИыЛд.эК╣эЮИ ъ┤СэММьЭШ ьД╕ъ╕░ыКФ ыСР ъ░АьзА ьаДъ│Д ъ╡мьД▒ьЪФьЖМьЭШ эБмъ╕░ ьаЬъ│▒эХйьЧР ы╣ДыбАэХйыЛИыЛд.
ъ╖╕ыЯмыВШ эММэШХьЭШ эО╕ъ┤С ьГБэГЬыКФ e ыМА eьЭШyx (ы│╡ьЮбэХЬ) ы╣ДьЬиьЧРызМ ьЭШьб┤эХйыЛИыЛд.ыФ░ыЭ╝ьДЬy e + e = 1ьЭ╕ эММэШХьЭДx ьГЭъ░БэХ┤ ы│┤ъ▓аьК╡ыЛИыЛд. ьЭ┤ыКФ ы╣И ( ( \ } \ _ьЧРьДЬ эПЙы░йып╕эД░ыЛ╣ ьХ╜ .00133ьЩАэК╕ьЭШ ъ░ХыПДьЧР эХ┤ыЛ╣эХйыЛИыЛд.ъ╖╕ыжмъ│а эО╕ъ┤С ьГБэГЬые╝ ыЕ╝эХа ыХМ эММэШХьЭШ ьаИыМА ьЬДьГБьЭА ьдСьЪФэХШьзА ьХКьЬ╝ыпАыбЬ eьЭШx ьЬДьГБьЭА 0, ьжЙx eыКФ ьЛдьИШьЭ┤ъ│аy eыКФ ы│╡ьЮбэХа ьИШ ьЮИыЛдъ│а эХШьЮР.ьЭ┤ыЯмэХЬ ьаЬэХЬ эХШьЧРьДЬ eьЩАy eыКФ ыЛдьЭМъ│╝x ъ░ЩьЭ┤ ыВШэГАыВ╝ ьИШ ьЮИьК╡ыЛИыЛд.
ьЧмъ╕░ьДЬ эО╕ъ┤С ьГБэГЬыКФ Q ъ░Т(-1 < Q < 1) ы░П ьГБыМА ьЬДьГБ{\(\ьЧР ьЭШэХ┤ ьЩДьаДэЮИ эММыЭ╝ып╕эД░эЩФ ыРйыЛИыЛд.
ы╣ДэЪбэММ
ьзДыПЩьЭА ьаДэММы░йэЦеьЧР ьИШьзБьЭ╕ ы░йэЦеьЬ╝ыбЬ эХЬьаХыРШьзА ьХКыКФ эММыПЩыПД ызОыЛд.ьЭ┤ыЯмэХЬ ьВмыбАыКФ ъ░АыбЬэММ(ы▓МэБм ып╕ыФФьЦ┤ьЭШ ыМАы╢Аы╢ДьЭШ ьаДьЮРэММ ыУ▒)ьЧР ь┤ИьаРьЭД ызЮь╢Ш эШДьЮм ъ╕░ьВмьЭШ ы▓ФьЬДые╝ эЫиьФм ы▓ЧьЦ┤ыВШьзАызМ, ы░йъ╕И эХЬ ъ▓Гь▓ШыЯ╝ Jones ы▓бэД░ые╝ ьВмьЪйэХШьЧм ъ░ДьДнэММьЭШ эО╕эММые╝ ъ░ДыЛиэЮИ ьДдыкЕэХа ьИШ ьЧЖыКФ ъ▓╜ьЪ░ьЧР ьЬаьЭШэХ┤ьХ╝ эХЬыЛд.
ьаДьЮРэММые╝ ъ│аыадэХШый┤ ьХЮьЧРьДЬ ьДдыкЕэХЬ ыВ┤ьЪйьЭА ъ╖аьЭ╝эХЬ ыУ▒ы░йьД▒ ы╣Дъ░РьЗа ыздь▓┤ьЭШ эПЙый┤эММьЧР ьЧДъ▓йэХШъ▓М ьаБьЪйыРШыКФ ы░Шый┤, ы╣ДыУ▒ы░йьД▒ ыздь▓┤ьЭШ ъ▓╜ьЪ░(ьХДыЮШьЧРьДЬ ьДдыкЕэХЬ ы│╡ъ╡┤ьаИ ъ▓░ьаХ ыУ▒) ьаДъ╕░ьЮе ыШРыКФ ьЮРъ╕░ьЮеьЭА ьвЕы░йэЦе ы░П эЪбы░йэЦе ъ╡мьД▒ьЪФьЖМые╝ ъ░АьзИ ьИШ ьЮИыЛд.ьЭ┤ ъ▓╜ьЪ░ ьаДъ╕░ы│АьЬД D ы░П ьЮРьЖНы░АыПД[clarification needed] BыКФ ьЧмьаДэЮИ ьГБъ╕░ эШХьГБьЭД ыФ░ые┤ьзАызМ эШДьЮм эЕРьДЬьЧР ьЭШэХ┤ ьг╝ьЦ┤ьзД ьаДъ╕░ьЮРэЩФьЬи(ыШРыКФ ьЮРъ╕░эИмъ│╝ьЬи)ьЭШ ьЭ┤ы░йьД▒ ыХМым╕ьЧР E(ыШРыКФ H)ьЭШ ы░йэЦеьЭ┤ D(ыШРыКФ B)ьЭШ ы░йэЦеъ│╝ ыЛдые╝ ьИШ ьЮИыЛд.ыУ▒ы░йьД▒ ыздь▓┤ьЧРьДЬыПД ъ╡┤ьаИыеаьЭ┤ [clarification needed]ъ╕ИьЖНъ│╝ ъ░ЩьЭА ьЬаьЭШэХЬ ъ░АьГБ ы╢Аы╢Д(ыШРыКФ "ьЖМый╕ ъ│ДьИШ")ьЭД ъ░АьзД ыздь▓┤ьЧР ьЖМьЬД ы╣Дъ╖аьзИэММъ░А ы░ЬьВмыРа ьИШ ьЮИыЛд. ьЭ┤ыЯмэХЬ ьЮеьЭА ьЧДы░АэХШъ▓М [9]: 179тАУ184 [10]: 51тАУ52 эЪбыЛиыРШьзАыПД ьХКыКФыЛд.ыПДэММъ┤А(ъ┤СьДмьЬа ыУ▒)ьЧРьДЬ ьаДэММыРШыКФ эСЬый┤эММ ыШРыКФ эММэШХьЭА ьЭ╝ы░ШьаБьЬ╝ыбЬ эЪбэММъ░А ьХДыЛИыЭ╝ ьаДъ╕░ ыШРыКФ ьЮРъ╕░ эЪбэММ ыкиыУЬ ыШРыКФ эХШьЭ┤ы╕МыжмыУЬ ыкиыУЬыЭ╝ъ│а эХа ьИШ ьЮИьК╡ыЛИыЛд.
ы╣И ъ│╡ъ░ДьЧРьДЬыПД эПЙый┤эММ ъ╖╝ьВмъ░А эММъ┤┤ыРШыКФ ь┤ИьаР ьШБьЧньЧРьДЬ ьвЕъ│Д ьД▒ы╢ДьЭД ы░ЬьГЭьЛЬэВм ьИШ ьЮИыЛд.ъ╖╣ыЛиьаБьЭ╕ ьШИыКФ ъ░Бъ░Б ьаДъ╕░ьЮе ыШРыКФ ьЮРъ╕░ьЮеьЭ┤ (ьаДэММ [11]ы░йэЦеьЭД ыФ░ыЭ╝) ьЩДьаДэЮИ ьД╕ыбЬьЭ╕ ы░йьВм ыШРыКФ ьаСьДа эО╕ъ┤СьЭ┤ыЛд.
ьЬаь▓┤ьдСьЭШ ьЭМэММыУ▒ьЭШ ьвЕэММьЭШ ъ▓╜ьЪ░, ьзДыПЩьЭШ ы░йэЦеьЭА ыЛ╣ьЧ░эЮИ ьзДэЦЙ ы░йэЦеьЭД ыФ░ые┤ыКФ ъ▓ГьЭ┤ъ╕░ ыХМым╕ьЧР, эО╕ъ┤СьЭШ ым╕ьаЬыКФ эЖ╡ьГБьЭА ьЦ╕ъ╕Йьб░ь░и ыРШьзА ьХКыКФыЛд.эХЬэО╕, ы▓МэБм ъ│аь▓┤ ыВ┤ьЭШ ьЭМэММыКФ ь┤Э 3ъ░ЬьЭШ эО╕эММ ьД▒ы╢ДьЬ╝ыбЬ ьвЕы░йэЦеы┐РызМ ьХДыЛИыЭ╝ эЪбы░йэЦеыПД ъ░АыКеэХШыЛд.ьЭ┤ ыХМ эЪбэО╕эММыКФ ьаДыЛиьЭСыае ы░П ьаДэММы░йэЦеъ│╝ ьИШьзБы░йэЦеьЬ╝ыбЬьЭШ ы│АьЬДы░йэЦеъ│╝ ъ┤АыаиьзАьЦ┤ьзАый░, ьвЕэО╕эММыКФ ъ│аь▓┤ьЭШ ьХХь╢Хъ│╝ ьаДэММы░йэЦеьЧР ыФ░ые╕ ьзДыПЩьЭД ыВШэГАыВ╕ыЛд.ьзАьзДэХЩьЧРьДЬыКФ ъ░АыбЬэО╕ъ┤Съ│╝ ьД╕ыбЬэО╕ъ┤СьЭШ ь░иы╢ДэПмъ░А ьдСьЪФэХШыЛд.
эО╕ъ┤С ьГБэГЬ
эО╕ъ┤СьЭА ь▓ШьЭМьЧРыКФ ьИЬьИШэХЬ эО╕ъ┤С ьГБэГЬьЩА ьЭ╝ы╢А ъ┤СэХЩ ьг╝эММьИШьЧРьДЬ ьЭ╝ъ┤АыРЬ ьВмьЭ╕эММызМ ъ│аыадэХиьЬ╝ыбЬьНи ъ░АьЮе ьЮШ ьЭ┤эХ┤эХа ьИШ ьЮИьК╡ыЛИыЛд.ьЭ╕ьаС ыЛдьЭ┤ьЦ┤ъ╖╕ыЮиьЭШ ы▓бэД░ыКФ ыЛиьЭ╝ ыкиыУЬ ыаИьЭ┤ьаАьЧРьДЬ ы░йь╢ЬыРШыКФ ьаДъ│ДьЭШ ы░ЬьзДьЭД ьДдыкЕэХа ьИШ ьЮИьК╡ыЛИыЛд(ы░ЬьзД ьг╝эММьИШыКФ ьЭ╝ы░ШьаБьЬ╝ыбЬ15 10ы░░ ы╣аыжЕыЛИыЛд).эХДыУЬыКФ эОШьЭ┤ьзАые╝ ыФ░ыЭ╝ x-y эПЙый┤ьЧРьДЬ ьзДыПЩэХШый░ эММэШХьЭА эОШьЭ┤ьзАьЧР ьИШьзБьЭ╕ z ы░йэЦеьЬ╝ыбЬ ьаДэММыРйыЛИыЛд.ьХДыЮШьЭШ ь▓ШьЭМ ыСР ъ╖╕ыж╝ьЭА ыСР ъ░АьзА ыЛдые╕ ы░йэЦеьЧРьДЬ ьДаэШХ эО╕ъ┤СьЭД ьЬДэХ┤ ьаДь▓┤ ьВмьЭ┤эБ┤ьЧР ъ▒╕ь│Р ьаДъ│Д ы▓бэД░ые╝ ь╢ФьаБэХйыЛИыЛд. ьЭ┤ыУдьЭА ъ░Бъ░Б ыЛдые╕ эО╕ъ┤С ьГБэГЬ(SOP)ыбЬ ъ░Дьг╝ыРйыЛИыЛд.45┬░ьЧРьДЬьЭШ ьДаэШХ эО╕эММыКФ ьИШэПЙ ьзБьДа эО╕эММ(ызи ьЩ╝ьк╜ ъ╖╕ыж╝ь▓ШыЯ╝)ьЩА ъ░ЩьЭА ьЬДьГБьЧРьДЬьЭШ ьИШьзБ эО╕эММьЭШ ь╢Фъ░АыбЬыПД ы│╝ ьИШ ьЮИьК╡ыЛИыЛд.
ьЭ┤ыЯмэХЬ ьИШэПЙ эО╕ъ┤С ьД▒ы╢Дъ│╝ ьИШьзБ эО╕ъ┤С ьД▒ы╢Д ьВмьЭ┤ьЧР ьЬДьГБ ы│АэЩФые╝ ыПДьЮЕэХШый┤ ьД╕ ы▓Иьз╕ ъ╖╕ыж╝ъ│╝ ъ░ЩьЭ┤ ьЭ╝ы░ШьаБьЬ╝ыбЬ эГАьЫР эО╕ъ┤СьЭД[12] ьЦ╗ьЭД ьИШ ьЮИьК╡ыЛИыЛд.ьЬДьГБ эО╕ь░иъ░А ьаХэЩХэЮИ ┬▒90┬░ьЭ┤ый┤ ьЫРэШХ эО╕эММъ░А ы░ЬьГЭэХйыЛИыЛд(4ы▓Иьз╕ ы░П 5ы▓Иьз╕ ъ╖╕ыж╝).ыФ░ыЭ╝ьДЬ ьЛдьаЬыбЬыКФ ьДаэШХ эО╕ъ┤СьЧРьДЬ ьЛЬьЮСэХШьЧм 1/4эММ эФМыаИьЭ┤эК╕ые╝ ьВмьЪйэХШьЧм ьЬДьГБ эО╕ъ┤СьЭД ыПДьЮЕэХШыКФ ьЫРэШХ эО╕ъ┤СьЮЕыЛИыЛд.ыСР ъ░ЬьЭШ ьЬДьГБ эО╕ьЭ┤ ьД▒ы╢ДьЭ┤ эЪМьаД ьаДъ│Д ы▓бэД░ые╝ ы░ЬьГЭьЛЬэВи ъ▓░ъ│╝ыКФ ьШдые╕ьк╜ ьХаыЛИыйФьЭ┤ьЕШьЧР ыВШьЩА ьЮИьК╡ыЛИыЛд.ьЫРэШХ ыШРыКФ эГАьЫР эО╕ъ┤СьЭА эХДыУЬьЭШ ьЛЬъ│Д ы░йэЦе ыШРыКФ ьЛЬъ│Д ы░ШыМА ы░йэЦе эЪМьаДьЭД ьИШы░ШэХа ьИШ ьЮИьК╡ыЛИыЛд.ьЭ┤ыКФ ьЬДьЭШ ыСР ьЫРэШХ эО╕ъ┤Съ│╝ ъ░ЩьЭА ыЪЬыа╖эХЬ эО╕ъ┤С ьГБэГЬьЧР эХ┤ыЛ╣эХйыЛИыЛд.
ым╝ыба ьЭ┤ ьДдыкЕьЧРьДЬ ьВмьЪйыРШыКФ xь╢Хъ│╝ yь╢ХьЭШ ы░йэЦеьЭА ьЮДьЭШьЮЕыЛИыЛд.ьЭ┤ыЯмэХЬ ьвМэСЬъ│Дые╝ ьДаэГЭэХШъ│а эО╕ъ┤С эГАьЫРьЭД x ы░П y эО╕ъ┤С ьД▒ы╢ДьЬ╝ыбЬ ы│┤ыКФ ъ▓ГьЭА ьЭ┤ыЯмэХЬ ъ╕░ьаА эО╕ъ┤СьЭШ ъ┤АьаРьЧРьДЬ Jones ы▓бэД░ьЭШ ьаХьЭШьЧР эХ┤ыЛ╣эХйыЛИыЛд.ьЭ╝ы░ШьаБьЬ╝ыбЬ xъ░А ьЮЕьВм эПЙый┤ьЧР ьЮИыКФ ъ▓Гъ│╝ ъ░ЩьЭА эК╣ьаХ ым╕ьаЬьЧР ьаБэХйэХШыПДыбЭ ь╢ХьЭД ьДаэГЭэХйыЛИыЛд.ьЮЕьВм эПЙый┤(p ы░П s эО╕эММ, ьХДыЮШ ь░╕ьб░)ъ│╝ ьзБъ╡РэХШыКФ ьДаэШХ эО╕эММьЧРыКФ ы│ДыПДьЭШ ы░ШьВм ъ│ДьИШъ░А ьЮИъ╕░ ыХМым╕ьЧР ьЭ┤ ьДаэГЭьЭА эСЬый┤ьЬ╝ыбЬы╢АэД░ьЭШ эММыПЩ ы░ШьВмьЭШ ъ│ДьВ░ьЭД эБмъ▓М ыЛиьИЬэЩФэХйыЛИыЛд.
ыШРэХЬ, ъ╕░ы│╕ эХиьИШыбЬ ьДаэШХ эО╕ъ┤Сы┐РызМ ьХДыЛИыЭ╝ ьзБъ╡Р эО╕ъ┤С ьГБэГЬьЭШ ыкиыУа ьМНьЭД ьВмьЪйэХа ьИШ ьЮИьК╡ыЛИыЛд.ьШИые╝ ыУдьЦ┤, ьШдые╕ьк╜ъ│╝ ьЩ╝ьк╜ьЭШ ьЫРэШХ эО╕ъ┤СьЭД ъ╕░ьаА эХиьИШыбЬ ьДаэГЭэХШый┤ ьЫРэШХ ы│╡ъ╡┤ьаИ(ъ┤СэХЩьаБ эЩЬыПЩ) ыШРыКФ ьЫРэШХ ьЭ┤ьГЙьД▒ъ│╝ ъ┤АыаиыРЬ ым╕ьаЬьЭШ эХ┤ы▓ХьЭД ыЛиьИЬэЩФэХа ьИШ ьЮИыЛд.
эО╕ъ┤С эГАьЫР
ьИЬьИШэХШъ▓М эО╕ъ┤СыРЬ ыЛиьГЙэММые╝ ьГЭъ░БэХ┤ ы┤ЕьЛЬыЛд.ызМьХ╜ эХЬ ьзДыПЩ ьВмьЭ┤эБ┤ьЧР ъ▒╕ь│Р ьаДъ│Д ы▓бэД░ые╝ эФМыбпэХЬыЛдый┤, ьЭ╝ы░ШьаБьЬ╝ыбЬ эГАьЫР эО╕ъ┤СьЭШ эК╣ьаХ ьГБэГЬьЧР эХ┤ыЛ╣эХШыКФ эГАьЫРьЭД ьЦ╗ьЭД ьИШ ьЮИьЭД ъ▓ГьЭ┤ыЛд.ьДаэШХ эО╕ъ┤Съ│╝ ьЫРэШХ эО╕ъ┤СьЭА эГАьЫР эО╕ъ┤СьЭШ эК╣ьИШэХЬ ъ▓╜ьЪ░ыбЬ ы│╝ ьИШ ьЮИьК╡ыЛИыЛд.
эО╕ъ┤С ьГБэГЬыКФ эГАьЫРьЭШ ъ╕░эХШэХЩьаБ эММыЭ╝ып╕эД░ьЩА ъ╖╕ "эХ╕ыУЬыЛИьКд" ьжЙ, эГАьЫРьЭД ьдСьЛмьЬ╝ыбЬ эХЬ эЪМьаДьЭ┤ ьЛЬъ│Ды░йэЦеьЭ╕ьзА ы░ШьЛЬъ│Ды░йэЦеьЭ╕ьзАьЧР ыМАэХ┤ ъ╕░ьИаэХа ьИШ ьЮИыЛд.эГАьЫРыПДэШХьЭШ эММыЭ╝ып╕эД░эЩФ ьдС эХШыВШыКФ эГАьЫРыеа ╬╕ = a/bьЩА эХиъ╗Ш эГАьЫРьЮеь╢Хъ│╝ Xь╢Х[13] ьВмьЭ┤ьЭШ ъ░БыПДыбЬ ьаХьЭШыРШыКФ ы░йэЦеъ░Б ╬╕ые╝ эГАьЫРьЮеь╢Хъ│╝ [14][15][16]ыЛиь╢ХьЭШ ы╣ДьЬиыбЬ ъ╖ЬьаХэХЬыЛд.(ь╢Х ы╣ДыЭ╝ъ│аыПД эХи)эГАьЫРьЭШ ы│ДыВи eьЭШ эГАьЫРьЬи ы│АьИШыКФ ыМАьХИьаБьЭ╕ parameterization=1тИТ b2/2,{\textstyle e={\sqrt{1-b^{2}{2}}},}ыШРыКФ эГАьЫР ыкиьЦС ъ░БыПД,╧З)arctan тБб b/{\textstyle\chi=\arctan b/a})arctan тБб 1/╬╡{\textstyle 1/\varepsilon=\arctan}ьЭА ъ╖╕ыж╝ьЧР ыВШэГАыВШ ьЮИыЛд.[13]ъ░БыПД ╬╕ыКФ ыШРэХЬ эС╕ьХ╡ь╣┤ыаИ ъ╡м(ьХДыЮШ ь░╕ьб░)ьЧР эСЬьЛЬыРЬ эО╕ъ┤С ьГБэГЬьЭШ ьЬДыПД(ьаБыПДыбЬы╢АэД░ьЭШ ъ░БыПД)ъ░А ┬▒2┬╡ьЩА ыПЩьЭ╝эХШыЛдыКФ ьаРьЧРьДЬ ьЬаьЭШэХШыЛд.ьДаэШХэО╕ъ┤Съ│╝ ьЫРэШХэО╕ъ┤СьЭШ эК╣ьИШэХЬ ъ▓╜ьЪ░ыКФ ым┤эХЬыМА ы░П ьЭ╝ь▓┤ьД▒ьЭШ эГАьЫРьД▒ ╬╕(0ъ│╝ 45┬░ьЭШ ╬╕)ьЧР эХ┤ыЛ╣эХЬыЛд.ъ░Бъ░Б ыЛдьЭМъ│╝ ъ░ЩыЛд.
ьб┤ьКд ы▓бэД░
ьЩДьаД эО╕ъ┤С ьГБэГЬьЧР ыМАэХЬ ьЩДьаДэХЬ ьаХы│┤ыКФ эО╕ъ┤Сый┤ ыВ┤ ьаДъ│Д ы▓бэД░ьЭШ 2ъ░Ь ьД▒ы╢ДьЧРьДЬьЭШ ьзДыПЩ ьзДэПнъ│╝ ьЬДьГБьЧР ьЭШэХ┤ьДЬыПД ьаЬъ│╡ыРЬыЛд.ьЭ┤ эСЬэШДьЭА эО╕ъ┤СьЭШ ыЛдые╕ ьГБэГЬъ░А ьЦ┤ыЦ╗ъ▓М ъ░АыКеэХЬьзАые╝ ы│┤ьЧмьг╝ъ╕░ ьЬДэХ┤ ьЬДьЧРьДЬ ьВмьЪйыРШьЧИьК╡ыЛИыЛд.ьзДэПн ы░П ьЬДьГБ ьаХы│┤ыКФ 2ь░иьЫР ы│╡ьЖМ ы▓бэД░(Jones ы▓бэД░)ыбЬ эО╕ыжмэХШъ▓М ыВШэГАыВ╝ ьИШ ьЮИьК╡ыЛИыЛд.
ьДЬ 1 a_ъ│╝ 2ыКФ ьаДъ│Д ы▓бэД░ьЭШ 2ъ░Ь ьД▒ы╢ДьЧРьДЬ эММэШХьЭШ ьзДэПньЭД ыВШэГАыВ┤ъ│а 1 _})ъ│╝ 2(\ _ыКФ ьЬДьГБьЭД ыВШэГАыГЕыЛИыЛд.ыЛиьЬДъ│ДьИШъ░А ы│╡ьЖМьИШьЭ╕ ьб┤ьКд ы▓бэД░ьЭШ ъ│▒ьЭА ъ░ЩьЭА эГАьЫРьЭД ыВШэГАыВ┤ыКФ ыЛдые╕ ьб┤ьКд ы▓бэД░ые╝ ьаЬъ│╡эХШыпАыбЬ эО╕ъ┤С ьГБэГЬъ░А ъ░ЩыЛд.ым╝ыжм ьаДьЮеьЭА ьб┤ьКд ы▓бэД░ьЭШ ьЛдьаЬ ы╢Аы╢ДьЬ╝ыбЬьДЬ ы│АэЩФэХШьзАызМ эО╕ъ┤С ьГБэГЬ ьЮРь▓┤ыКФ ьаИыМА ьЬДьГБъ│╝ыКФ ыПЕыж╜ьаБьЮЕыЛИыЛд.ьб┤ьКд ы▓бэД░ые╝ ыВШэГАыВ┤ъ╕░ ьЬДэХ┤ ьВмьЪйыРШыКФ ъ╕░ьаА ы▓бэД░ыКФ ьДаэШХ эО╕ъ┤С ьГБэГЬые╝ ыВШэГАыВ╝ эХДьЪФъ░А ьЧЖыЛд(ьжЙ, ьЛдьЮмэХЬыЛд).ьЭ╝ы░ШьаБьЬ╝ыбЬ ьзБъ╡Р ы▓бэД░ ьМНьЭ┤ 0ьЭШ ыВ┤ьаБьЭД ъ░ЦыКФ ъ▓ГьЬ╝ыбЬ ьаХьЛЭьЬ╝ыбЬ ьаХьЭШыРШыКФ 2ъ░ЬьЭШ ьзБъ╡Р ьГБэГЬые╝ ьВмьЪйэХа ьИШ ьЮИыЛд.ьЭ╝ы░ШьаБьЭ╕ ьДаэГЭьЭА ьвМьЪ░ ьЫРэШХ эО╕эММьЭ┤ыЛд. ьШИые╝ ыУдьЦ┤ ьЫРэШХ ы│╡ъ╡┤ьаИ ыздь▓┤(ьХДыЮШ ь░╕ьб░) ыШРыКФ ьЫРэШХ эО╕эММьЧР ып╝ъ░РэХЬ ъ░ДьДньД▒ ъ▓Аь╢Ьъ╕░ьЭШ ьЛаэШ╕ ъ▓╜ыбЬьЧРьДЬ ьЭ┤ыЯмэХЬ ыСР ъ░АьзА ъ╡мьД▒ьЪФьЖМьЭШ эММыПЩ ьаДэММые╝ ыкиыН╕ызБэХШыКФ ъ▓ГьЭ┤ыЛд.
ьвМэСЬ эФДыаИьЮД
эО╕ъ┤С ьГБэГЬъ░А ъ╕░эХШэХЩьаБ эММыЭ╝ып╕эД░ьЩА ьб┤ьКд ы▓бэД░ые╝ ьВмьЪйэХШьЧм эСЬэШДыРШыУа ьГБъ┤АьЧЖьЭ┤ эММыЭ╝ып╕эД░эЩФьЧРьДЬ ьХФым╡ьаБьЬ╝ыбЬ ыВШэГАыВШыКФ ъ▓ГьЭА ьвМэСЬ эФДыаИьЮДьЭШ ы░йэЦеьЭ┤ыЛд.ьЭ┤ъ▓ГьЭА ьЦ┤ыКР ьаХыПДьЭШ ьЮРьЬаыПД, ьжЙ ьаДэММ ы░йэЦеьЧР ыМАэХЬ эЪМьаДьЭД ъ░АыКеэХШъ▓М эХЬыЛд.ьзАъ╡м эСЬый┤ъ│╝ эПЙэЦЙэХШъ▓М ьаДэММыРШыКФ ы╣ЫьЭД ъ│аыадэХа ыХМ, "ьИШэПЙ"ъ│╝ "ьИШьзБ" эО╕ъ┤СьЭ┤ыЭ╝ыКФ ьЪйьЦ┤ъ░А ьвЕьвЕ ьВмьЪйыРШый░, ьаДьЮРыКФ ьб┤ьКд ы▓бэД░ьЭШ ь▓л ы▓Иьз╕ ьД▒ы╢Д, ьжЙ 0 ы░йьЬДъ░Бъ│╝ ъ┤АыаиьЭ┤ ьЮИьК╡ыЛИыЛд.эХЬэО╕, ь▓Ьым╕эХЩьЧРьДЬыКФ ьаБыПД ьвМэСЬъ│Дъ░А ьЭ╝ы░ШьаБьЬ╝ыбЬ ьВмьЪйыРШый░, ьаХы╢БьЧР ыМАьЭСэХШыКФ ьаЬыбЬ ы░йьЬДъ░Б(ыШРыКФ ьИШэПЙ ьвМэСЬъ│ДьЩА эШ╝ыПЩьЭД эФ╝эХШъ╕░ ьЬДэХ┤ ь▓Ьым╕эХЩьЧРьДЬ ыНФ ьЭ╝ы░ШьаБьЬ╝ыбЬ ы╢Аые┤ыКФ ьЬДь╣Ш ъ░БыПД)ьЭ┤ ьВмьЪйыРйыЛИыЛд.
s ы░П p ьзАьаХ
ьЮРьг╝ ьВмьЪйыРШыКФ ыШР ыЛ