2

← 1 2 3 →
−1 0 1 2 3 4 5 6 7 8 9 → 수 목록 정수 ← 0 10 20 30 40 50 60 70 80 90 →
추기경	두명
서수	2차(2차/2차)
수 체계	이진법의
인수분해	초특급의
가우시안 정수 인수분해	${\displaystyle (1+i)(1-i)}$
프라임	첫 번째
나눗셈	1, 2
그리스 수	β'
로마 숫자	II, II
그리스어 접두어	디-
라틴어 접두어	2인조/2인조
고대 영어 접두어	두 번의
이진법	102
테르나리	23
세니어	26
팔달	28
십이진법	212
16진수	216
그리스 수	β'
아랍어, 쿠르드어, 페르시아어, 신디어, 우르두어	٢
세상에	፪
벵골어	২
중국어 숫자	二，弍，貳
데바나가르 ī	२
텔루구	౨
타밀어	௨
칸나다	೨
히브리어	ב
아르메니아어	Բ
크메르어	២
마야숫자	••
타이어	๒
그루지야인	ⴁ/ⴁ/ბ(바니)
말라얄람어	൨
바빌로니아 수	𒐖
이집트 상형문자, 에게 숫자, 중국산 계수봉
모스 부호	.._ _ _

2(2)는 숫자, 숫자, 숫자입니다. 다음 1과 앞 3의 자연수입니다. 그것은 가장 작고 유일한 소수입니다. 이중성의 기초를 이루기 때문에 많은 문화권에서 종교적이고 정신적인 의미가 있습니다.

진화

아라비아숫자

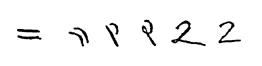
현대 서구 세계에서 숫자 2를 나타내기 위해 사용된 숫자는 그 뿌리를 인디크 브라흐미 문자로 거슬러 올라가며, 여기서 "2"는 두 개의 수평선으로 쓰여졌습니다. 현대의 중국어와 일본어는 여전히 이 방법을 사용합니다. 굽타 스크립트는 두 선을 45도 회전시켜 대각선으로 만들었습니다. 상단 라인은 또한 때때로 짧아지고 하단 곡선이 하단 라인의 중앙을 향해 있습니다. 나가리 대본에서는 윗줄이 아랫줄과 연결되는 곡선처럼 쓰여 있었습니다. 아랍어 구바르 문자에서 밑줄은 완전히 수직이고, 숫자는 점 없는 종결 물음표처럼 보였습니다. 하단선을 원래의 수평 위치로 복원하되 상단선을 하단선과 연결되는 곡선으로 유지하는 것이 우리의 현대적인 숫자로 이어집니다.^[1]

텍스트 도형이 있는 글꼴에서 숫자 2는 일반적으로 x-높이입니다. 예를 들어,^{[citation needed]}

한마디로

2는 가장 일반적으로 이틀 안에 이 두 가지를 선택할 때처럼 복수의 셀 수 있는 명사와 함께 사용되는 결정자입니다.^[2] 2 더하기 2가 4인 것처럼 숫자 2를 지칭할 때 2는 명사입니다.

2의 어원

2라는 단어는 고대 영어 단어인 twā(여성), tu(중성자), two(남성)에서 유래되었습니다.^[3]

발음 /tu ː/와 같은 발음은 w에 의한 모음의 불안정화로 인한 것으로 관련된 소리 앞에서 사라졌습니다. 따라서 Old English twa의 연속적인 발음 단계는 /tw ɑː/, /tw ɔː/, /tw ː/, /twu ː/, 그리고 마지막으로 /tu ː/입니다.

수학

특성화

숫자 2는 가장 작고 짝수인 소수입니다. 가장 작은 소수로서, 2는 0이 아닌 가장 작은 소수이며, 유일한 소수입니다.^[4] 정수는 2로 나눌 수 있는 경우에도 짝수로 결정됩니다. 소수와 같은 짝수를 기준으로 숫자 체계로 작성된 정수의 경우 맨 끝자리만 보고 2로 나눌 수 있는 가분성을 쉽게 검사할 수 있습니다. 짝수이면 전체 숫자가 짝수입니다. 십진법으로 쓰여지면 2의 모든 배수는 0, 2, 4, 6, 8로 끝납니다.^[5]

1보다 큰 모든 정수는 적어도 두 개의 다른 요인을 갖습니다. 정의에 따르면 소수는 두 개의 다른 요인(자체 및 1)만 갖습니다. 따라서, 양의 $정수{\displaystyle }$ n ${\displaystyle$ n$}$의 $함수{\displaystyle }$(${\displaystyle n)}$ ${\displaystyle d(n))$는 다음을$$ 만족합니다.

${\displaystyle 여기서\; liminf}$ ${\displaystyle \liminf}$는(최대 2개의 약수를 갖는 더 큰 소수가 항상 존재하기 때문에) 하위 한계를 나타냅니다$$.^[6]

구체적으로.

자연수의 집합론적 구성에서 2 ${\displaystyle 2}$은(는) $집합${∅ $},$ ∅ } ${\displaystyle \{\{\varnothing$ $\backslash \},\backslash$varnothing$\}$로 식별되며, $여기$서 ∅ ${\$displaystyle \varnothing}은(는) 빈 집합을 나타냅니다. 이 후자의 집합은 범주 이론에서 중요합니다. 집합의 범주에서 하위 개체 분류기입니다. 더 넓게는 필드인 집합에는 최소 두 개의 요소가 있습니다.

2진법은 반지름이 2이고, 그리고 자연수를 ($n개$의 ($n개의)$ 토큰을$$ 가진) 단일 토큰의 해당 카운트로 직접 표현하는 것보다 (${\displaystyle {로그\mathrm{}}_{}}$ 2 ${\$ $n개$의 ${\displaystyle$ $n$$}$개의$$ 토큰으로) 실질적으로 더 간결하게 표현할 수 있는 가장 적은 토큰을 가진 숫자 시스템입니다. 이 숫자 시스템은 컴퓨팅에 광범위하게 사용됩니다.^{[citation needed]}

0보다 큰 차원의 유클리드 공간에서 평면 내의 두 개의 서로 다른 점은 항상 고유한 선을 정의하기에 충분합니다.^{[citation needed]}

칸토어 공간

칸토어 공간은 칸토어 집합과 동형인 위상 공간 ${\displaystyle {2N\mathbb{}}^{}}$ ${\$ 2$^{\mathbb {N}}}$이며, 일반 집합은 경계점으로만 구성된 닫힌 집합입니다. 가장 단순한 이산 2점 공간인 $\{{\displaystyle 0,}$ 1${\displaystyle \}}$ ${\displaystyle \{0,1$의 셀 수 없는 무한 곱 토폴로지는 칸토어 공간의 전통적인 기본 예입니다. Points whose initial conditions remain on a ${\displaystyle [0,1]}$ boundary in the logistic map ${\displaystyle x_{n+1}=rx_{n}(1-x_{n})}$ form a Cantor set, where values begin to diverge beyond ${\displaystyle r=4.}$ Between ${\displaystyle r\approx 3.$$45}$ 및 $3{\displaystyle .57}$ ${\displaystyle$ 3$.57$ 모집단은 혼돈이 발생하기 전에 $8{\displaystyle ,}$ ${\displaystyle 16,}$ ${\displaystyle ...,}$ ${\displaystyle {2n}^{}\dots ,}$ $2개$$∞$ ${\displaystyle$8,$16, ...,$2^{$n},\ldots,2^{\$infty } 값 사이의 진동에 접근합니다.

2의 거듭제곱

2는 첫 번째 메르센 소수 지수이고, 처음 두 페르마 소수 (3과 5) 사이의 차이입니다. 2의 거듭제곱은 컴퓨터 과학에서 필수적이며 기본 도구를 사용하여 규칙적인 다각형을 구성하는 데 중요합니다(예: 페르마 또는 피어퐁 소수 사용). ${\displaystyle 2}$ ${\displaystyle$ 2$}$는 자연력의 역수의 합이 자신과 동일한 유일한 숫자입니다. 기호로 표시하면,

${\displaystyle \sum _{n=0}^{\infty }{\frac {1}{2^{n}}}=1+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+\cdots =2.}$

2는 또한 $2{\displaystyle }$+ ${\displaystyle 2}$ = 2${\displaystyle }$× ${\displaystyle 2}$ = ${\displaystyle {}^{}}$ = ${\displaystyle 2^{}}$ ↑↑ ${\displaystyle 2}$ = ${\displaystyle 2}$ = ${\displaystyle 2}$ ↑↑↑${\displaystyle }$.${\displaystyle 2+2$=$2\times$ 2=$2^{2$} = 2$\uparrow \uparrow 2$=$2\uparrow \uparrow$2={\$text{ }}...$$}$모든 수준의 하이퍼 연산을 통해$$ 여기서는 크누스의 위쪽 화살표 표기법으로 표시되며 모두 $4$와 같습니다${\displaystyle \mathrm{.}}$ ${\displaystyle$ 4$.}$

특히 파스칼 삼각형의 행 합은 연속적인 거듭제곱인 2, ${\displaystyle {2n}^{}}$과 동치입니다${\displaystyle {}^{}}$ ${\displaystyle 2^{n}}$

정수 수열

숫자 2와 3은 연속적인 정수이기도 한 유일한 두 소수입니다. 2는 차이가 2인 제대로 된 쌍둥이 소수가 없는 첫 번째 소수이고, 3은 쌍둥이 소수가 5인 첫 번째 소수입니다.^[9][10] 결과적으로 3과 5는 2의 제곱인 2, ${\displaystyle {22\mathrm{}}^{}}$ ${\$ 사이에 4를 포함합니다$.$ 이것들은 또한 소수이면서 동시에 고도로 합성된 두 개의 유일한 4개의 고도로 합성된 수(1, 2, 4, 6)^[11] 중 하나인 홀수 소수이기도 합니다.^[12] Furthermore, ${\displaystyle (3,5)}$ are the unique pair of twin primes ${\displaystyle (q,q+2)}$ that yield the second and only prime quadruplet ${\displaystyle (11,13,17,19)}$ that is of the form ${\displaystyle (d-4,d-2,d+2,d+4)}$, 여기서 $d{\displaystyle }$ ${\displaystyle d}$는 해당 트윈 프라임의 곱입니다.^[13]

다른 중요한 정수 수열 안에서는

${\displaystyle 2}$ ${\displaystyle 2}$은(는) 가장 작은 기본 의사 완전수이며,^[24] Mertens 함수에 대해 0을 반환하는 첫 번째 숫자입니다.^[25] 최소 퍼펙트 수, 유니터리 퍼펙트 수,$$ $1$보다 큰 오레 수 $$등 $6개{\displaystyle \mathrm{}}$ ${\displaystyle 6}$의 약수의 조화 평균도 2 ${\displaystyle 2}$입니다$.$ 특히 0이 아닌 모든 삼각수의 역수의 합은 2로 수렴합니다.^[26] 반면, 숫자는 마법 상수를 산출하는 ${\displaystyle 2}$× 2 ${\displaystyle$ 2$\times 2}$ 마법$$ 사각형에 배치될 수 없으며, 따라서 숫자는 n ${\displaystyle n}$ x$$ $n{\displaystyle }$ ${\displaystyle n}$ 마법$$ 사각형 집합 중 유일한 $null$입니다.^[27][a] 알려진 숭고한 수는 단 두 개로, 완전한 수의 인자를 가진 수이며, 그 합 자체가 완전한 수를 산출합니다.^[28]

후자는 76자리 길이(10진수 표시)의 숫자입니다.

Bernouilli 번호 $B{\displaystyle {}_{}}$ ${\displaystyle {\mathrm{2k}}_{}}$ ${\$에$$대해 규칙 $2{\displaystyle \mathrm{}}$ ${\displaystyle 2}$의 불규칙성은${\displaystyle \mathrm{-1입니다.}}$ ${\displaystyle -1.}$

반복수열

$\{{\displaystyle 0\}}$ ${\displaystyle$T}부터$$ 이진 부울 상보체에 연속적으로 인접하는$$Thue-Morse $시퀀스{\displaystyle }$ T ${\displaystyle T}$에서 ($연속적으로)$ 임계 지수, 또는 인접한 하위 시퀀스가 반복되는 가장 큰 횟수는 $2{\displaystyle \mathrm{}}$ ${\displaystyle 2}$입니다$.$ where there exist a vast amount of square words of the form ${\displaystyle ww.}$^[30] Furthermore, in ${\displaystyle c}$, which counts the instances of ${\displaystyle 1}$ between consecutive occurrences of ${\displaystyle 0}$ in ${\displaystyle T}$ that is instead square-free, $c$ =