Step-by-Step Guide: How to Find the Area of an Octagon
In geometry, an Octagon is defined as a regular polygon with 8 sides and 8 interior angles.
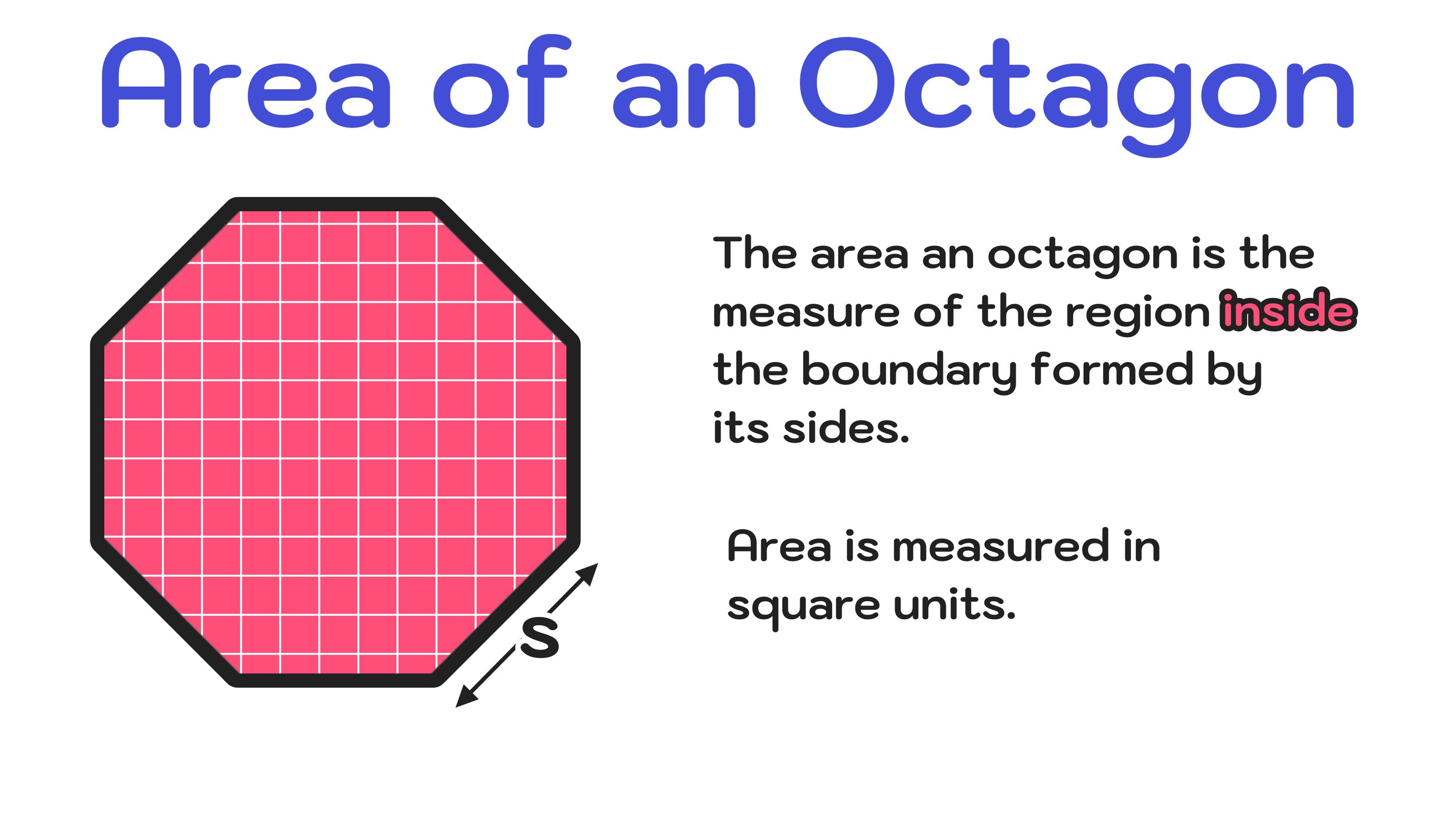
The area of an octagon is the measure of all of the space within the region enclosed by an octagon’s 8 sides. The area of an octagon is dependent on its size (i.e. the larger an octagon’s size, the larger its area will be). Additionally, the area of an octagon is always expressed using square units (this is the case for the area of any two dimensional geometric figure).
(Are you looking for an area of an octagon calculator? Click here to access our free Area of an Octagon Calculator)
The following step-by-step guide on how to calculate the area of an octagon will cover the following:
Figure 01: What is the area of an octagon?
What is the area of a polygon? The area of any polygon (including the area of octagon) is the measure of the space contained inside of the boundary formed by its sides. The area of octagon can be determined by dividing the figure into smaller/simpler shapes (namely triangles and rectangles) and calculating the collective sum of their individual areas. Again, the area of an octagon is always expressed in terms of units squared or square units (e.g. square feet, square yards, square inches, etc)
A stop sign is a regular octagon.
Calculating the area of an octagon is a relatively simple process provided that you know how to use the area formula of octagon. This standard area of octagon formula can be used to calculate the area of any regular octagon (an eight-sided figure with eight sides that have equal lengths). The most common real-world figure that is a regular octagon is a stop sign.
(All of the octagons referenced in this guide are regular octagons that have 8 sides of equal length and 8 interior angles of equal measure.
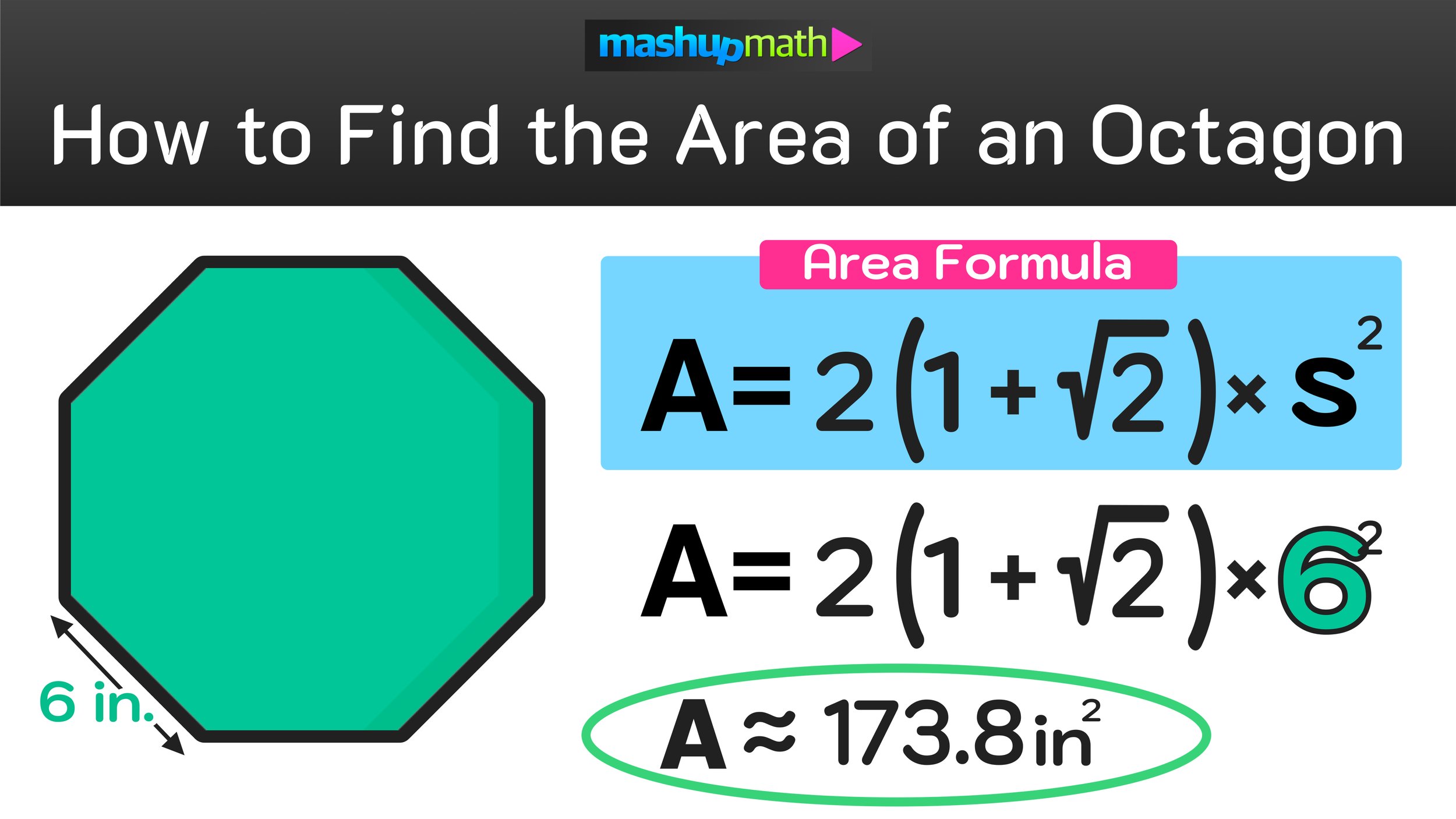
Figure 02: What is the area of an octagon formula? The formula for the area of an octagon is A = 2(1+ √2) x s^2
One can calculate the area of an octagon by using the formula for the area of an octagon: A = 2(1+ √2) x s^2, where the area, A , equals the measure of all of the space contained by the sides of the octagon and s equals the side length.
Learning how to calculate the area of an octagon is an essential mathematics skill that you can learn quickly and easily by applying a simple 3-step method for calculating the area of an octagon.
Here are the 3-steps for finding the area of an octagon:
Step One: Determine the value of s, the length of each side of the octagon
Step Two: Input the value of s into the area of octagon formula A = 2(1+ √2) x s^2 and solve for A
Step Three: Express the final answer in terms of square units
As an example, you can determine that the area of an octagon where each side is 6 inches long by substituting s=6 into the area formula of octagon and then solving for A. This process is shown in Figure 03 below:
Figure 03: How to Find the Area of an Octagon
Step One: Determine the value of s, the length of each sides of the octagon
Again, since the octagon has sides that are each 6 inches long, you can conclude that s=6
Step Two: Input the value of s into the area of octagon formula A = 2(1+ √2) x s^2 and solve for A
For the second step, substitute s=6 into the area formula of octagon as shown below:
A = 2(1+ √2) x s^2 → A = 2(1+ √2) x 6^2 ≈ 173.82338
Step Three: Express the final answer in terms of square units
For the third and final step for finding the area of an octagon, you have to express the result in terms of units squared
Final Answer: The area of an octagon with a side length of 6 inches is approximately 173.8 in^2.
Figure 04: The area of octagon when s=6 is approximately 173.8 square inches.
If you can learn to apply the previously mentioned 3-step process for calculating the area of an octagon using the area formula of an octagon, you can use it to accurately solve any problem that requires to find the area of an octagon with a given side length.
The best way to learn the process is through practice, so let’s gain some more experience using it by working through some area of an octagon example problems in the next section.
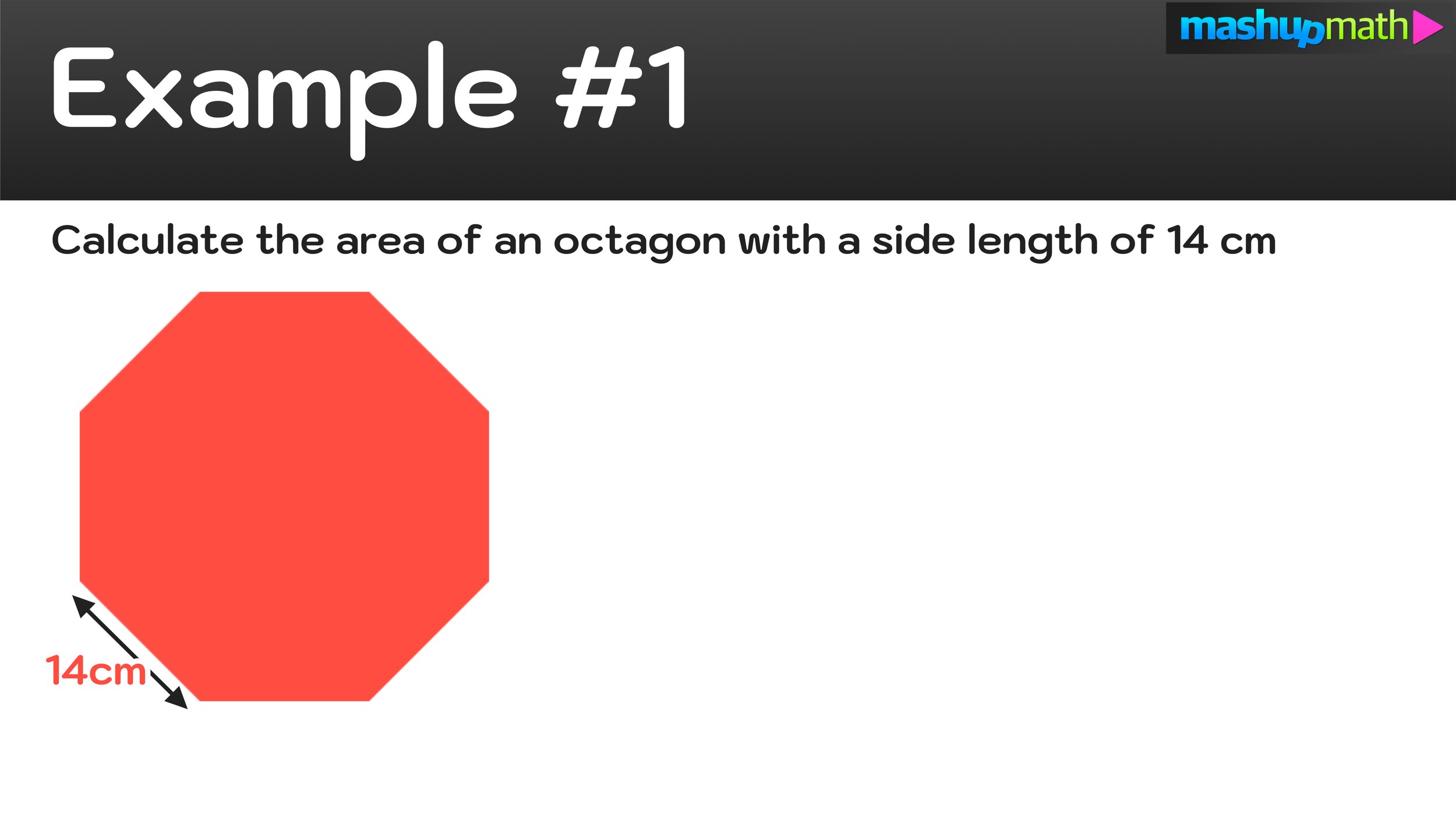
Example #1: Find the area of an octagon with a side length of 14 centimeters
Finding the area of an octagon when s=14, you can simply apply the three steps shown in the previous section of this guide.
Step One: Determine the value of s, the length of each sides of the octagon
In this first example, the octagon has a side length of 14cm, so s=14
Step Two: Input the value of s into the area of octagon formula A = 2(1+ √2) x s^2 and solve for A
Next, plug s=14 into the octagon area formula as follows:
A = 2(1+ √2) x s^2 → A = 2(1+ √2) x 14^2 ≈ 946.37172
Step Three: Express the final answer in terms of square units
Finally, you can express the area of an octagon with a side length of 14 centimeter using square units as follows:
Final Answer: The area of an octagon with a side length of 14 centimeters is approximately 946.4 cm^2
Example #1 Solved: Calculate the area of an octagon when s=14
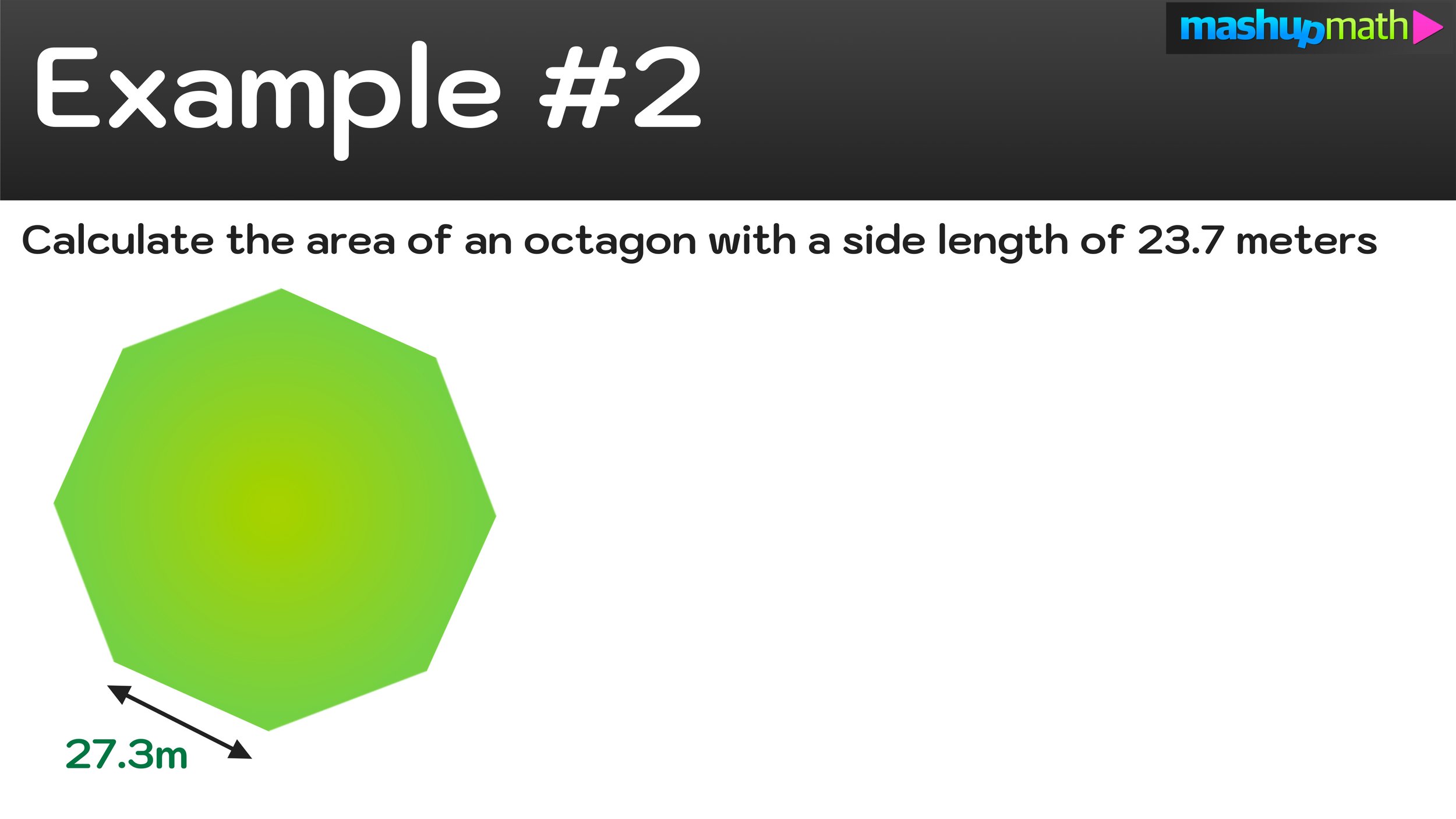
Example #2: How to Find the Area of a Octagon
Similar to Example #1, you can find the area of this octagon by applying the same three step process:
Step One: Determine the value of s, the length of each sides of the octagon
The side length of this octagon is 27.3 meters, therefore s=27.3
Step Two: Input the value of s into the area of octagon formula A = 2(1+ √2) x s^2 and solve for A
Now, plug s=27.3 into the octagon area formula as follows:
A = 2(1+ √2) x s^2 → A = 2(1+ √2) x 27.3^2 ≈ 3598.57845
Step Three: Express the final answer in terms of square units
For the last step, express your answer using square units.
Final Answer: The area of an octagon with a side length of 27.3 meters is approximately 3,598.6 m^2
Example #2 Solved: The area of an octagon with a side length of 23.7 meters is approximately 3,598.6 square meters.
Are you looking for a way to quickly and correctly calculate the area of an octagon without doing the calculations by hand? If so, you can use our free Area of an Octagon Calculator, which is a very handy math tool that you can use to rapidly find the area of any regular octagon with a known side length. The calculator is also a great tool for checking your work and ensuring that your manual calculations are accurate.
To use the free calculator, simply input the value of s and press ENTER or DONE to calculate the octagon’s area in square units.
You can calculate the area of an octagon with a known side length of s, by using the octagon area formula A = 2(1+ √2) x s^2, where A equals the area of the octagon.
You can calculate the area of any regular octagon by following these three steps:
Step One: Determine the value of s, the length of each sides of the octagon
Step Two: Input the value of s into the area of octagon formula A = 2(1+ √2) x s^2 and solve for A
Step Three: Express the final answer in terms of square units
Search Tags: area of a n octagon, area of an octagon, area of octagon, the area of a octagon, area of a octagon, area formula of octagon, area of octagon formula, formula for the area of an octagon, area formula of an octagon, calculate the area of an octagon, how to find an area of an octagon, area formula of a octagon, calculate area of a octagon