Asteroid "Apophis" (2004 MN4)
Bruce L. Gary
Links internal to this web page:
Brightness
revision
suggestion
Rotation light curve: roation
period and
shape ratio
BRIGHTNESS
REVISION SUGGESTION
2005.02.05
This web page section shows observations of asteroid "2004 MN4" that
have
been calibrated using Tycho stars in the same images used for
observing the
asteroid (71 x 47 'arc). All-sky photometry was attempted on several
occasions
but the atmospheric extinction was too variable due to scattering
from cirrus
clouds. I conclude that this asteroid is ~0.3 magnitude brighter
than the
ephemeris value of H = 19.3, i.e., I suggest that H = 19.0. Details
are given
below.
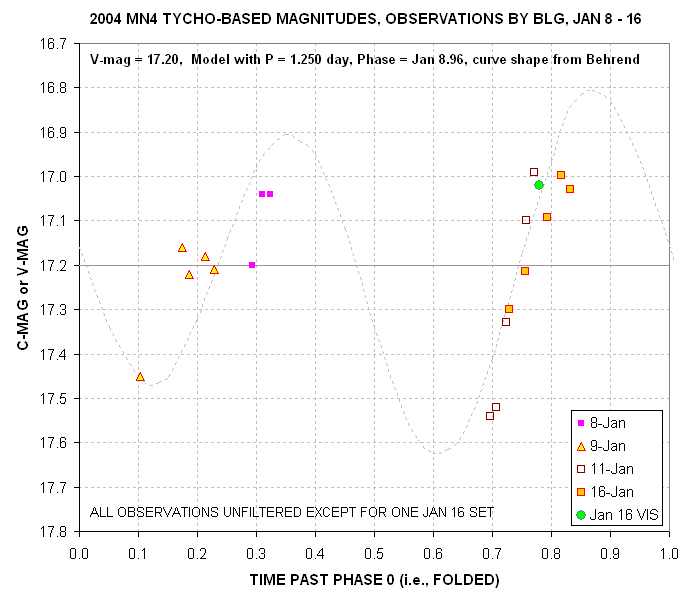
Figure 1. Plot of V-equivalent magnitudes for
asteroid "20044
MN4" based on Tycho stars in the same image as the asteroid. No
adjustments
have been made to achieve a fit to the model curve, which is based
on the
analysis of Dr. Raoul Behrend. The period for this plot is 1.250
days instead
of Behrend's 1.2764 days. The green symbol was made using a
V-filter, the
others were unfiltered. Changes in apparent brightness due to
changing distance
from Earth have been removed in a way that renders the plot valid
for January
16. A known instrumental sensitivity to star color has been
applied to the
asteroid using an assumed B-V = 0.80.
For each observing date several Tycho stars were used to
establish a calibration for that night's images. All but one
observing set were unfiltered.
Instrumental corrections for unfiltered observations have been
established
on many nights with this observing system, and the conversion from
star flux
to equivalent V-magnitude, called C-mag, has been found to obey the
following
relationship:
C-mag = 21.37 - 2.5 * LOG ( Fv / g ) - Kv * m +
0.30 *
(B-V-0.64) + 0.04 * m * (B-V-0.64),
where
Fv = flux (using a V-filter), g = exposure time [seconds], Kv =
zenith extinction
(using a V-filter) [mag/air mass], and m = air mass.
On photometric nights Kv = 0.12 [mag/air mass]. On non-photometric
nights
it is higher, and must be established using either Tycho stars or
nearby
Landolt stars. For these observations Tycho stars were used for
calibration,
and they don't have reliable B-V colors, so I assumed they were
typical in
having B-V = 0.64 (the average of all 1259 Landolt stars). The
asteroid is
assumed to be redder than typical stars, with B-V = 0.80 +/- 0.05
(as suggested
by Prof. Richard Binzel). One V-filter observation confirms the
unfiltered
results taken a few minutes earlier.
The ephemeris currently uses H = 19.3. The magnitudes in the
above
plot were adjusted to be valid for January 16, when the ephemeris
predicts
a V-magnitude of 17.53. The asteroid appears to be brighter by 0.33
magnitude,
implying that H = 18.97.
The uncertainty on this suggested value for H depends upon the
validity of
G. But for now, let us adopt the ephemeris value of G = 0.15. Tthe
main uncertainty
would then come from the measurements presented here. The assumed
B-V for
the asteroid produces an uncertainty of only 0.004 magnitude (i.e.,
assuming
B-V = 0.80 +/- 0.05). Another source of uncertainty is the use of
Tycho stars
with unknown B-V. Since different Tycho stars were used for each
observation
night, and since an average of 3 such stars were averaged, it can be
estiamted
that the average of 4 observing nights (12 Tycho stars) introduces
an uncertainty
of ~ 0.03 magnitude for the average magnitude of 17.20 (this is
based on
an estiamted RMS on B-V for Tycho stars ~ 0.3 magnitude and a star
color sensitivity
of 0.30). This is probably the principal systematic error source for
the
observations reported here. Another source of uncertainty relates to
the
way I used a model rotational light curve for fitting the
observations. If,
for example, all observations were at the peak brightness part of
such a
light curve then it is obvious that the asteroid's average
brightness would
be over-estimated. However, in this case most of the measurements
were made
during the rising portion of the light curve. I estimate that this
source
of uncertainty is ~0.05 magnitude. Finally, stochastic uncertainty
("noise")
is present, but with SNR typically > 50 for each data group shown
in the
above plot this source of uncertainty is estiamted to be < 0.02
magnitude.
I conclude by suggesting that the value for H be revised from 19.3
to 19.0
+/- 0.10, subject to the assumption that G = 0.15.
__________________ The remainder of this web page was
created inJanuary,
and was a vehicle for presenting observations by two observer
groups
_________________________
ASTEROID "2004
MN4" ROTATION
LIGHT CURVE
Bruce L. Gary and Vishnu V. Reddy
2004.01.15
Introduction
Near Earth Object asteroid "2004 MN4" was discovered last June, was
lost,
then was recovered in November. By December 23 the orbit had been
established
well enough by NASA's Near Earth Object Program Office at JPL that
the NEO
Program Office (Yeomans, Chesly and Choda) posted at MPML that a
near Earth
pass in 2029, April 13 had a 1 in 300 chance of Earth impact.
Because of
the December 27 re-assessment of a 1 in 37 chance of Earth impact in
2029
an effort was made to refine the orbit with new astrometry
observations.
Finally, the Spacewatch telescope at Kitt Peak found an image of the
asteroid
(mag 22) taken in March (before the discovery) showing an asteroid
position
that was quickly incorporated into orbit calculations that reduced
the probability
of Earth impact to near zero. Nevertheless, the pass in 2029 will
occur, and
the asteroid may pass close enough (8 Earth radii) to be visible
with the
naked eye.
There has been considerable discussion on the MPML about photometry
shortcomings,
and the need for better brightness values in order to estimate
asteroid size.
Radar observations are planned, and part of the planning requires
approximate
maximum Doppler width from the returned echo. Therefore, to assist
in radar
planning it is important to obtain brightness measurements that are
not only
accurate but precise enough to establish a rotation period.
On January 6 Raoul Behrend reported to the MPML that Yassine
Damerdji had
obtained observations at Haute-Provence Observatory from which a
rotation
light curve was derived. The light curve solution (by Damerdji et
al)
calls for a period of 0.6 +/- 0.4 day (14.4 +/- 9.6 hours) and an
amplitude
of 0.2 mag (half of peak-to-peak variation). The light curve can be
found
at http://obswww.unige.ch/~behrend/page5cou.html#04m04n.
January 8 and 9 Light Curve Observations
On UT dates January 8, 9 and 11 Vishnu V. Reddy (University of
North
Dakota graduate student) and Ken Archer (Ironwood Observatory,
Hawaii) used the 10-inch Takahashi Baker-RC f/5 telesope and SBIG
ST8 CCD of the Ironwood
Observatory, Hawaii (F60) to observe 2004 MN4. These observations
were conducted
remotely from North Dakota by VVR using the Share My Sky
program.
On January 8, 9 and 11 Bruce Gary observed "MN4" using the Hereford
Arizona
Observatory (G95) Celestron 14-inch SCT and SBIG ST-8XE CCD. The
January
9 and 11 observations were made through cirrus clouds with
extinction variations
of 0.6 magnitude. Our data have been combined and are shown in the
following
figure.
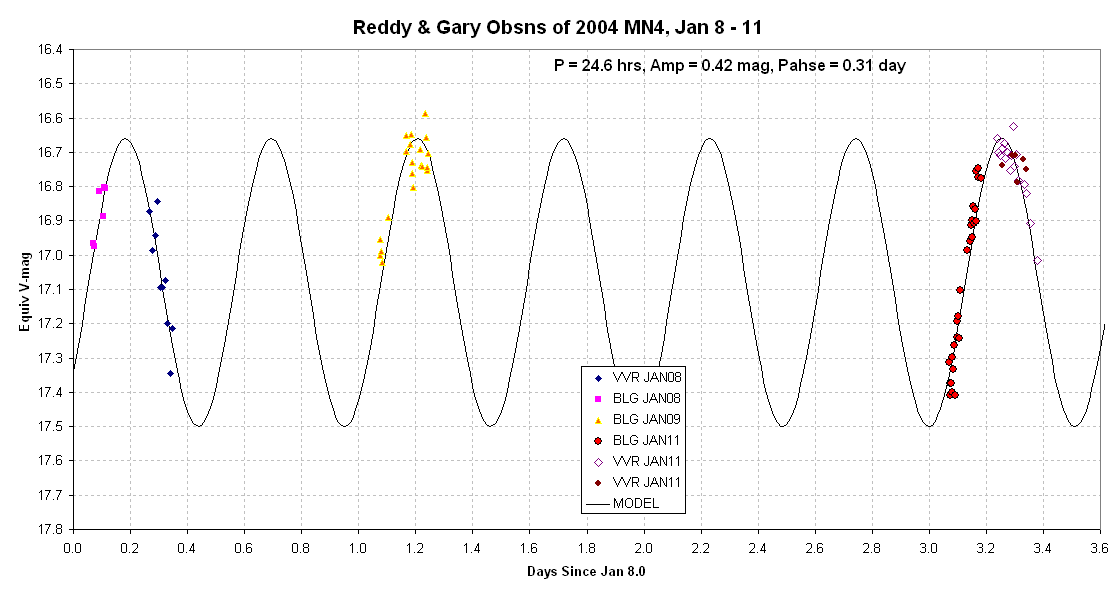
Figure 1. Equivalent V-magnitudes (from unfiltered
observations)
during a 4-day observing interval. The magnitude scale is set by a
January
11 image (by BLG) with several Tycho stars in the same FOV as the
asteroid.
All other data sets were zero-shifted to agree with the BLG Jan 11
data.
The BLG observations (at Hereford Arizona Observatory, G95) were
made by
Bruce L. Gary with a 14-inch Celestron and SBIG ST-8XE CCD, and
were processed
by median combining sets of three 60-second exposures using
the asteroid
for alignment. The VVR observations (at Ironwood
Observatory, Hawaii,
F60) are 5-point averages of 60-second exposures.
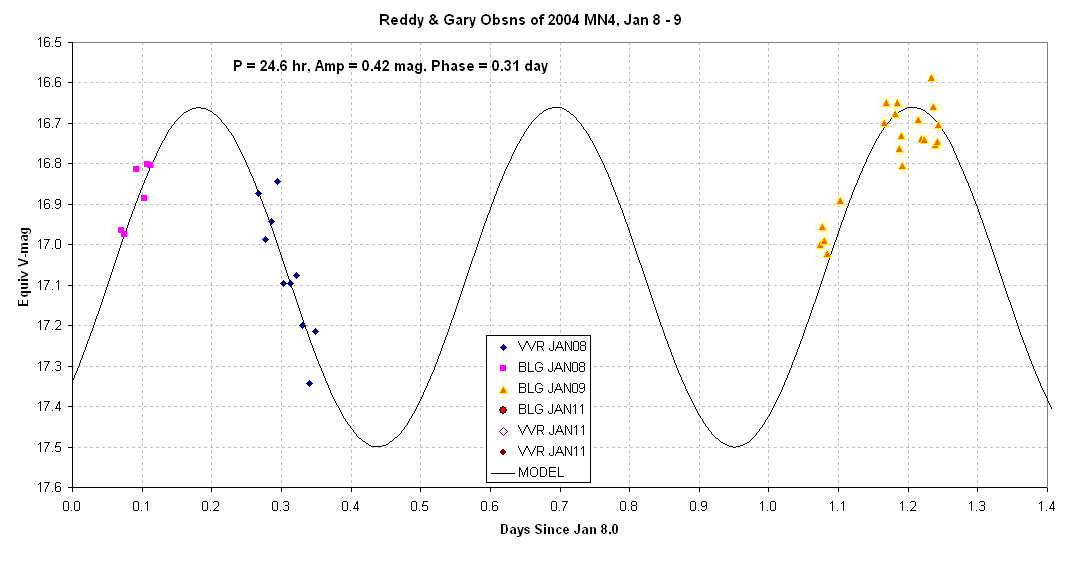
Figure 2. Same as previous figure except showing only
the
Jan 8 and 9 observations.
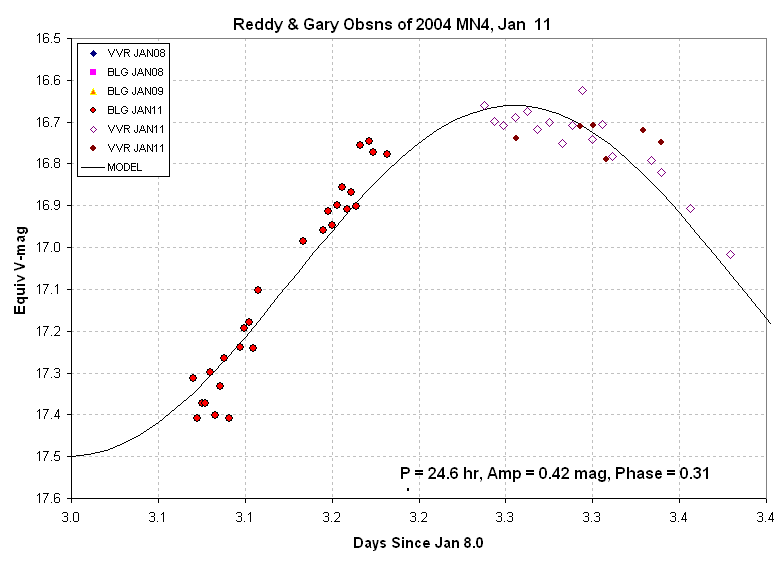
Figure 3. Same as first figure except showing only
the Jan
11 observations.
The fitted sinusoidal model solution has two periods per
rotation period.
The rotation period from this data (alone) is estimated to be ~24.6
hours.
The amplitude (half of peak-to-peak) is 0.42 magnitude. I hesitate
to give
SE uncertainties since I've been wrong about this several times in
the past
week.
Note that using a sinusoid is just a first approximation for fitting
an asteroid
rotation light curve. Shape matters, and all real asteroid shapes
produce
light curve shapes that depart from sinusoidal.
Analysis Procedure Used by BLG
The procedure used by BLG for reducing images to asteroid magnitudes
involves
two analysis phases. The first phase transfers magnitudes from Tycho
stars
in the FOV to secondary stars near the asteroid's path. The second
phase
uses these secondary calibration stars to determine the magnitude of
the
asteroid in sets of 3 median combined images.
The first phase consists of the following: calibrate raw images
(dark and
flat), median combine neighbor sets of 3 images using stars for
alignment
(MCs images), median combine the same 3 images using the asteroid
for alignment
(MCa images), read intensity of MCs Tycho stars for several images,
determine
extinction and zero-shift parameter in a spreadsheet, use these
extinction
and zero-shift values to determine magnitude of stars near the
asteroid's
path, adopt the average magnitude for these secondary calibration
stars for
use as reference stars.
The second phase consists of the following: perofrm two median
combines
for each set of 3 images, one aligned using the asteroid and the
other aligned
using the stars. Intensity readings are made of the (three)
secondary reference
stars on the MCs images, and intensity readings are made of the
asteroid
on the MCa iamges (placing the photometry pattern so as to minimize
the influence
of background level biases). These intensity readings are entered in
a spreadsheet that has been prepared for this specific analysis
procedure. A block of cells
for each image is used to establish an extinction for that image in
a way
that produces reference star magnitudes that agree (on average) with
those
adopted in the first phase of analysis (taking into account the
image's air
mass). The zero-shift and extinction values allow for a conversion
of the
asteroid's intensity to be converted to a magnitude.
This analysis procedure may be unique in the way it allows for
asteroid motion
between images. Notice that all intensity readings are done with
images that
have cosmic ray defects removed and SNR enhanced by median
combining. Also
note that the median combining is performed separately for images
intended
for reference star intensity readigns and asteroid intensity
readings. This
median combining using the asteroid for alignment requires that the
asteroid
can be seen in each image, which places a practical limit on how
faint the
asteroid can be for using the procedure. For an asteroid moving at
the rate
of 2004 MN4 when these observations were made (~3.8 "arc/minute) the
longest
exposure time for avoiding oval asteroid source functions was 60
seconds
for my image scale of 2.8 "arc/pixel. For a 14-inch aperture
telscope and
50-second exposures the faintest asteroid for which this method can
work
is about V-mag = 18. For a larger telescope, such as 32-inch
aperture, the limiting asteroid magnitude ~ 20 (unless sophisticated
techniques are used
to anticipate the asteroid's pixel location.)
Raoul Behrend's Analysis
Raoul Behrend has combined this data with measurements by Yassine
Damerdji
and the early data by VVR and BLG to produce a new period of 22.97
+/- 0.14
hours. The amplitude for the solution of the data in the previous
figure
(0.27 +/- 0.10 magnitude) is compatible with the 0.3 +/- ~0.05
magnitude
amplitude given by Behrend using the combined data. The combined
data calculated
by Raoul Behrend can be found at Raoul
Behrend's rotation
light curves . The light curve solution at this site is likely
to change
as new observations are added to the analysis.
Here's my version of Raoul Behrend's rotational light curve period
of 1.2733
+/- 0.0026 days, fitted to the data available to me (VVR and BLG).
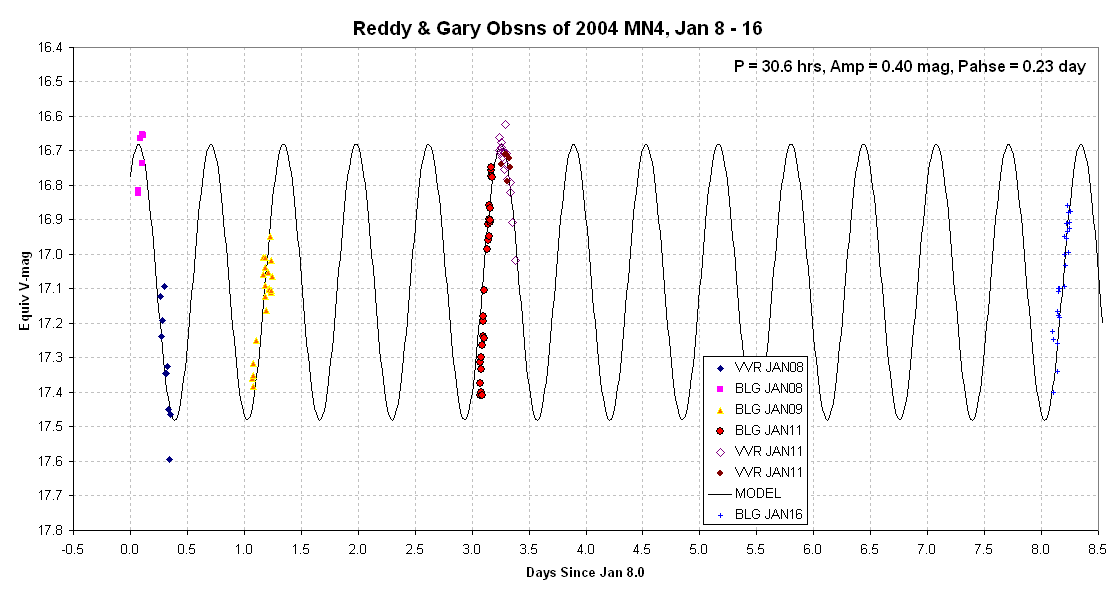
Figure 4. Adopting Raoul Behrend'srotation period
solution of
1.2733 days (30.6 hours) and allowing for zero-offset adjustemtns,
it is
possible to achieve an acceptable fit to the VVR and BLG
observations.

___________________________________________________________
This site opened: January 9, 2005. Last Update: February 5, 2005